Частина 4

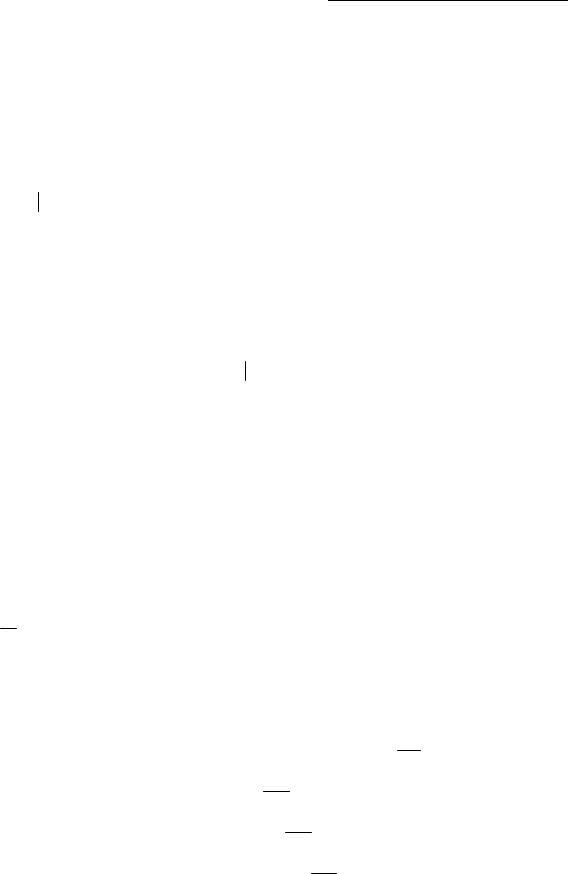
“Курс вищої математики. Частина 4.”

Абсолютний центральний момент першого порядку називається середнім арифметичним відхиленням.

Приклад. Для вище за приклад визначити математичне очікування і дисперсію випадкової величини Х.

D( X ) = M (X 2 ) −[M ( X )]2 = 0,1163 −0 = 0,1163.

Приклад. У урні 6 білих і 4 чорних кулі. З неї п'ять разів підряд витягують кулю, причому кожного разу вийняту кулю повертають назад і кулі перемішують. Прийнявши за випадкову величину Х число білих куль, що витягують, скласти закон розподілу цієї величини, визначити її математичне очікування і дисперсію.

Оскільки кулі в кожному досвіді повертаються назад і перемішуються, то випробування можна вважати незалежними (результат попереднього досвіду не впливає на ймовірність появи або непояви події в іншому досвіді).

Таким чином, ймовірність появи білої кулі в кожному досвіді постійна і рівна

PБ = 106 = 0,6.

Таким чином, в результаті п'яти послідовних випробувань біла куля може не з'явитися зовсім, з'явитися один раз, два, три, чотири або п'ять разів.

Для складання закону розподілу треба знайти ймовірність кожної з цих подій. 1) Біла куля не з'явилася зовсім: РБ (0) = (1 − РБ )5 = 0,0102.

2) Біла куля з'явилася один раз: РБ (1) = С51 РБ1 (1 − РБ )4 = 1!54!!0,6 0,44 = 0,0768

3)Біла куля з'явитися двічі: PБ (2) = 2!5!3!0,62 0,43 = 0,2304 .

4)Біла куля з'явитися три рази: РБ (3) = 3!5!2!0,63 0,42 = 0,3456.

5)Біла куля з'явитися чотири рази: РБ (4) = 4!5!1!0,64 0,41 = 0,2592.

6)Біла куля з'явилася п'ять разів: РБ (5) = 0,65 = 0,0778.

Отримуємо наступний закон розподілу випадкової величини Х.

31

“Курс вищої математики. Частина 4.”

M ( X ) = 0,0768 + 2 0,2304 +3 0,3456 + 4 0,2592 +5 0,0778 = 3,0002.

M ( X 2 ) = 0,0768 + 4 0,2304 +9 0,3456 +16 0,2592 + 25 0,0778 =10,201. D(X ) = M (X 2 ) −[M (X )]2 =10,201 −9,0012 =1,1998.

При вирішенні практичних завдань часто точно знайти закон розподілу випадкової величини досить складно. Проте, всі процеси, що відбуваються, пов'язані з випадковими величинами, можна розділити на декілька типів, кожному з яких можна поставити у відповідність який – або закон розподілу.

Вище були розглянуті деякі типи розподілів дискретної випадкової величини такі як біномінальний розподіл і розподіл Пуассона.

Розглянемо тепер деякі типи законів розподілу для безперервної випадкової величини.

Рівномірний розподіл.

Визначення. Безперервна випадкова величина має рівномірний розподіл на відрізку [а, b], якщо на цьому відрізку щільність розподілу випадкової величини постійна, а поза ним рівна нулю.

Постійна величина З може бути визначена з умови рівності одиниці площі, обмеженої кривої розподілу.

f(x)

C = b −1 a

Отримуємо C = b −1 a .

Знайдемо функцію розподілу F(x) на відрізку [а,b].

32

“Курс вищої математики. Частина 4.”

F(x)

1

Для того, щоб випадкова величина підкорялася закону рівномірного розподілу необхідно, щоб її значення лежали усередині деякого певного інтервалу, і усередині цього інтервалу значення цієї випадкової величини були б рівноімовірні.

Визначимо математичне очікування і дисперсію випадкової величини, підпорядкованої рівномірному закону розподілу.

Ймовірність попадання випадкової величини в заданий інтервал:

Показовий розподіл.

Визначення. Показовим (експоненціальним) називається розподіл ймовірності безперервної випадкової величини Х, яке описується щільністю

33

“Курс вищої математики. Частина 4.”

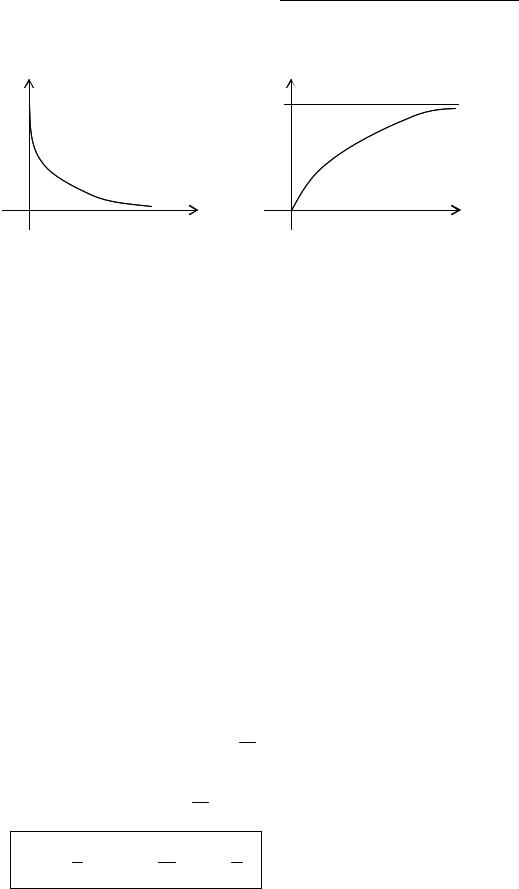
Графіки функції розподілу і щільності розподілу:

Знайдемо математичне очікування випадкової величини, підпорядкованої показовому розподілу.

Для знаходження дисперсії знайдемо величину М(Х2).

∞∞

M ( X 2 ) = ∫x2 f (x)dx = ∫λx2 e−λx dx

Двічі інтегруючи по частинах, аналогічно розглянутому випадку, отримаємо:

M ( X 2 ) = λ22 ;

Тоді D( X ) = M (X 2 ) −[M ( X )]2 = λ12 .

Разом: M ( X ) = λ1 ; D( X ) = λ12 ; σx = λ1 .

Видно, що у разі показового розподілу математичне очікування і середнє квадратичне відхилення рівні.

34

“Курс вищої математики. Частина 4.”

Також легко визначити і ймовірність попадання випадкової величини, підпорядкованої показовому закону розподілу, в заданий інтервал.

P(a < x < b) = F(b) − F(a) = e−λa −e−λb .

Показовий розподіл широко використовується в теорії надійності.

Допустимо, деякий пристрій починає працювати у момент часу t0=0, а через какое– той час t відбувається відмова пристрою.

Позначимо Т безперервну випадкову величину – тривалість безвідмовної роботи пристрою.

Таким чином, функція розподілу F(t)= P(T<t) визначає ймовірність відмови за час тривалістю t.

Ймовірність протилежної події (безвідмовна робота протягом часу t) рівна R(t)=

P(T>t)= 1 – F(t).

Визначення. Функцією надійності R(t) називають функцію, що визначає ймовірність безвідмовної роботи пристрою протягом часу t.

Часто на практиці тривалість безвідмовної роботи підкоряється показовому закону розподілу.

Взагалі кажучи, якщо розглядати новий пристрій, то ймовірність відмови на початку його функціонування буде більша, потім кількість відмов знизиться і якийсь час матиме практично одне і те ж значення. Потім (коли пристрій виробить свій ресурс) кількість відмов зростатиме.

Іншими словами, можна сказати, що функціонування пристрою впродовж всього існування (у сенсі кількості відмов) можна описати комбінацією двох показових законів (на початку і кінці функціонування) і рівномірного закону розподілу.

Функція надійності для какогоабо пристрою при показовому законі розподілу

рівна:

R(t) =1 − F(t) = e−λt .

Дане співвідношення називають показовим законом надійності.

Важливою властивістю, що дозволяє значно спростити вирішення завдань теорії надійності, є те, що ймовірність безвідмовної роботи пристрою на інтервалі часу t не залежить від часу попередньої праці до початку даного інтервалу, а залежить тільки від тривалості часу t.

Таким чином, безвідмовна робота пристрою залежить тільки від інтенсивності відмов λ і не залежить від безвідмовної роботи пристрою у минулому.

Оскільки подібною властивістю володіє тільки показовий закон розподілу, то цей факт дозволяє визначити, чи є закон розподілу випадкової величини показовим чи ні.

Нормальний закон розподілу.

Визначення. Нормальним називається розподіл ймовірності безперервної випадкової величини, яке описується щільністю ймовірності

35

“Курс вищої математики. Частина 4.”

Нормальний закон розподілу також називається законом Гауса.

Нормальний закон розподілу займає центральне місце в теорії ймовірності. Це обумовлено тим, що цей закон виявляється у всіх випадках, коли випадкова величина є результатом дії великого числа різних чинників. До нормального закону наближається решта всіх законів розподілу.

Можна легко показати, що параметри mx іσx , вхідні в щільність розподіли є

відповідно математичним очікуванням і середнім квадратичним відхиленням випадкової величини Х.

Знайдемо функцію розподілу F(x).

Графік щільності нормального розподілу називається нормальній кривій або кривій Гауса.

Нормальна крива володіє наступними властивостями: 1) Функція визначена на всій числовій осі.

2) При всіх х функція розподілу приймає тільки позитивні значення.

3) Вісь ОХ є горизонтальною асимптотою графіка щільності ймовірності, оскільки при необмеженому зростанні по абсолютній величині аргументу х, значення функції прагне до нуля.

4) Знайдемо екстремум функції.

5)Функція є симетричною відносно прямою х = а, оскільки різниця (х – а) входить у функцію щільності розподілу в квадраті.

6)Для знаходження точок перегину графіка знайдемо другу похідну функції щільності.

При x = m + σ і x = m - σ друга похідна рівна нулю, а під час переходу через ці крапки міняє знак, тобто в цих крапках функція має перегин.

σe 12π .

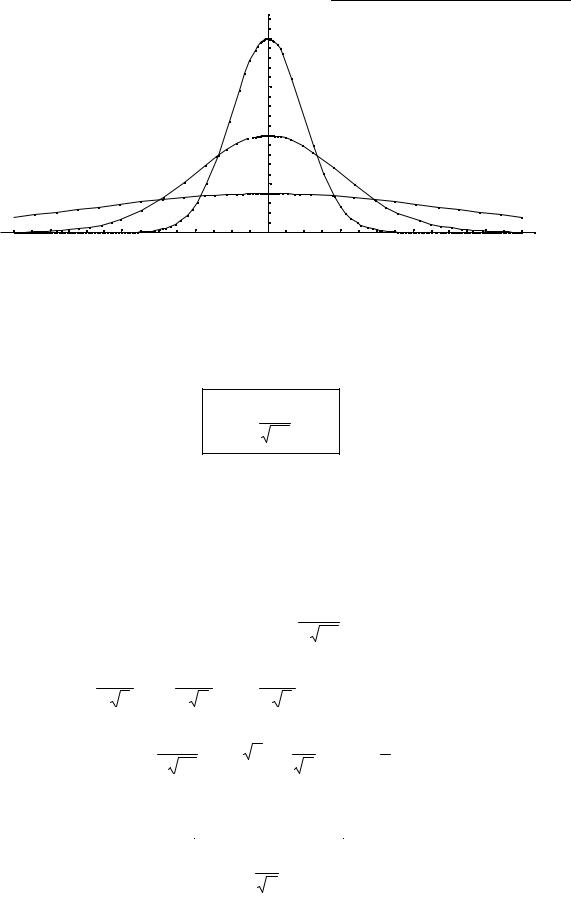
Побудуємо графік функції щільності розподілу.

36

Побудовані графіки при т =0 і трьох можливих значеннях середнього квадратичного відхилення σ = 1 = 2 і σ = 7. Як видно, при збільшенні значення середнього квадратичного відхилення графік стає пологішим, а максимальне значення зменшується..

Якщо а > 0, то графік зміститься в позитивному напрямі, якщо а < 0 – в негативному.

При а = 0 і σ = 1 крива називається нормованою. Рівняння нормованої кривої:

ЛЕКЦІЯ 5.

Функція Лапласа.

Знайдемо ймовірність попадання випадкової величини, розподіленої по нормальному закону, в заданий інтервал.

Оскільки інтеграл ∫e−t 2 dt не виражається через елементарні функції, то вводиться в

розгляд функція

яка називається функцією Лапласа або інтегралом ймовірності.

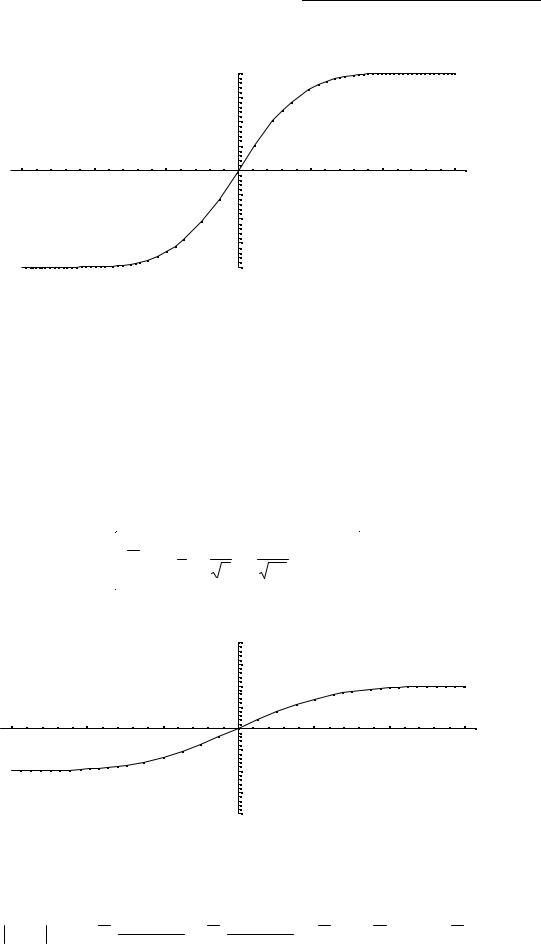
Значення цієї функції при різних значеннях х пораховані і приводяться в спеціальних таблицях.

37

“Курс вищої математики. Частина 4.”

Якщо прийняти ∆ = 3σ, то отримуємо з використанням таблиць значень функції Лапласа:

P( X − m < 3σ) = 2Φ(3) = 2 0,49865 = 0,9973

Тобто ймовірність того, що випадкова величина відхилиться від свого математичного очікування на величину, велику чим потрійне середнє квадратичне відхилення, практично рівна нулю.

Це правило називається правилом трьох сигм.

Не практиці вважається, що якщо для якої – або випадкової величини виконується правило трьох сигм, то ця випадкова величина має нормальний розподіл.

Приклад. Поїзд складається з 100 вагонів. Маса кожного вагону – випадкова величина, розподілена по нормальному закону з математичним очікування а = 65 т і середнім квадратичним відхиленням σ = 0,9 т. Локомотив може везти склад масою не більше 6600 т, інакше необхідно причіплювати другий локомотив. Знайти ймовірність того, що другий локомотив не буде потрібно.

Другий локомотив не буде потрібно, якщо відхилення маси складу від очікуваного (10065 = 6500) не перевершує 6600 – 6500 = 100 т.

Оскільки маса кожного вагону має нормальний розподіл, то і маса всього складу теж буде розподілена нормально.

Отримуємо:

P( X − M ( X ) <100 = 2Φ 100 = 2Φ[1,111]= 2 0,3665 = 0,733100σ

Приклад. Нормально розподілена випадкова величина Х задана своїми параметрами – а =2 – математичне очікування і σ = 1 – середнє квадратичне відхилення. Потрібно написати щільність ймовірності і побудувати її графік, знайти ймовірність того, Х прийме значення з інтервалу (1; 3), знайти ймовірність того, що Х відхилиться (по модулю) від математичного очікування не більше ніж на 2.

Щільність розподілу має вигляд:

Знайдемо ймовірність попадання випадкової величини в інтервал (1; 3).

39

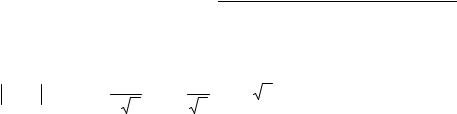
“Курс вищої математики. Частина 4.”

Знайдемо ймовірність відхилення випадкової величини від математичного очікування на величину, не велику чим 2.

Той же результат може бути отриманий з використанням нормованої функції Лапласа.

Центральна гранична теорема Ляпунова.

Теорема. Якщо випадкова величина Х є сумою дуже великого числа взаємно незалежних випадкових величин, вплив кожній з яких на всю суму нікчемно мало, то Х має розподіл, близький до нормального.

На практиці для більшості випадкових величин виконуються умови теореми Ляпунова.

Система випадкових величин.

Розглянуті вище випадкові величини були одновимірними, тобто визначалися одним числом, проте, існують також випадкові величини, які визначаються двома, трьома і так далі числами. Такі випадкові величини називаються двовимірними, тривимірними і так далі

Залежно від типу, вхідних в систему випадкових величин, системи можуть бути дискретними, безперервними або змішаними, якщо в систему входять різні типи випадкових величин.

Детальніше розглянемо системи двох випадкових величин.

Визначення. Законом розподілу системи випадкових величин називається співвідношення, що встановлює зв'язок між областями можливих значень системи випадкових величин і ймовірністю появи системи в цих областях.

Визначення. Функцією розподілу системи двох випадкових величин називається функція двох аргументів F(x, у), рівна ймовірності сумісного виконання двох нерівностей X<x, Y<y.

F(x, y) = P(X < x,Y < y)

Відзначимо наступні властивості функції розподілу системи двох випадкових величин:

1) Якщо один з аргументів прагне до плюс нескінченність, то функція розподілу системи прагне до функції розподілу однієї випадкової величини, відповідної іншому аргументу.

2) Якщо обидва аргументи прагнуть до нескінченності, то функція розподілу системи прагне до одиниці.

F(∞, ∞) =1;

40