Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Sb96063

.pdf

Скачиваний:

Добавлен:

13.02.2021

Размер:

886.23 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

						x7			2x6 3x5 4x4 5x3 6x2 7x 8
																																																	dx
																					x2 1 4																												dx
																					x2 1 4
								x		15			7						x		5		16				x		3					1			x	2			17			x				7
								x			4			dx				4	x					3			x								2		x					4		x				6		.
											4							4						3											2							4						6
									2																			x
									2																												3
								x 1																								2					1
								x 1																								2
					Вычислим оставшийся интеграл:
	x				15																																						d x2 1
										1							2x							15 dx															1													15
					4					1							2x							15 dx															1													15
							dx													dx																																			arctg(x)
x2 1							dx					2				x2 1				dx				4						x2 1										2					x2 1								4		arctg(x)
		1		ln x2					1					15			arctg(x) c.
	2			ln x2					1				4				arctg(x) c.
	2												4
					Итоговый ответ:																	x7			2x6								3x5						4x4 5x3 6x2 7x 8																		dx
					Итоговый ответ:																																				x2 1 4																dx
																																									x2 1 4
																								7				x			5					16		x	3				1		x		2	17				x		7
			1	ln x2					1						15		arctg(x)
			1												15											4											3						2								4			6		c.
																																						x2 1																		c.
	2												4																									x2 1
	2												4																																	3

1.2.6. Интегрирование тригонометрических функций

Рассмотрим на примерах несколько основных приемов интегрирования тригонометрических функций.

1. Интегралы от функций вида sin m (x) cosn (x).

sin x

Пример 16. Вычислить cos2 x dx .

Если хотя бы одна из степеней нечетная, можно сделать замену y sin x или y cos x (заменяем ту функцию, которая входит в подынтегральное выражение в четной степени).

sin x		y cos x	dy	1		1
	dx				c		c.
cos2 x	dx		y 2		c		c.
cos2 x	dy sin x dx		y 2	y		cos x

Пример 17. Вычислить sin 2 x dx .

Если обе степени четные, предварительно нужно применить формулы понижения степени.

Формулы понижения степени: sin 2 x					1 cos(2x)	,	cos2 x				1 cos(2x)	.
Формулы понижения степени: sin 2 x					2	,	cos2 x				2	.
					2						2
sin 2 x dx	1 cos(2x)	dx	1	( 1dx cos(2x)dx)				x	1	sin(2x) c.
sin 2 x dx		dx		( 1dx cos(2x)dx)						sin(2x) c.
	2		2				2		4

Пример 18. Вычислить sin(5x) cos(x)dx .

Если подынтегральное выражение – произведение синусов или косинусов разных аргументов, то подынтегральное выражение можно упростить при по-

мощи формул тригонометрии:	sin x sin y	1	cos(x y) cos(x y) ,
		2

cos x cos y

cos(x y) cos(x y) , sin x cos y

sin( x y) sin( x y) .

sin(5x) cos(x)dx

sin(4x) sin(6x) dx

cos(4x)

cos(6x) c.

Пример 19. Вычислить

dx .

1 8 cos x

Если подынтегральная функция – рациональная функция от sin x, cos x , то соответствующий интеграл сводится к интегралу от рациональной функции

при помощи универсальной тригонометрической замены

y tg(

) . При этом

dy dx , а основные тригонометрические функции выражаются так:

2(1 y2 )

sin x

2 y

, cos x

1 y

1 y2

y tg(

)

1 y

cos x

dy .

9 7 y2

8cos x

1 y2

2(1 y2 )

Таким образом, исходный интеграл сведен к интегралу от дробно-рацио- нальной функции, техника вычисления таких интегралов подробно рассмотрена ранее.

									1
1				1					1				1					1						1				3 7 y

			9 7 y2			dy										dy						dy					ln			c =
2			9 7 y2					12 3						7 y				3		7 y				12 7				3	7 y
							x

1				3	7tg(				)

		ln					2			c.

12 7							x

				3	7tg(			)
				3	7tg(		2	)
																									x


												1						1			3		7 tg(			)
	Итоговый ответ:											1			dx			1	ln		3		7 tg(		2	)	c.
																									x

											1 8cos x						12 7
											1 8cos x						12 7
																					3		7 tg(			)
																					3		7 tg(		2	)

Разумеется, перечисленными приемами способы интегрирования тригонометрических функций не исчерпываются. Рассмотрены лишь наиболее распространенные.

2.ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

2.1.Определение и свойства определенного интеграла

Пусть	функция	f (x)	определена на			отрезке	[a;b]	и
a x0 x1 ... xn b ,		тогда интегралом функции				f (x) на отрезке		[a;b]
		b		n 1
				n 1			ti [xi ; xi 1],
называется	число	f (x)dx lim i 0 f (ti ) xi ,				где	ti [xi ; xi 1],
		a	max	xi	0

xi xi 1 xi .

Число a называется нижним пределом интегрирования, а число b – верхним пределом интегрирования.

Обратите внимание, что результат вычисления неопределенного интеграла – функция, а результат вычисления определенного интеграла – число.

		Простейшие свойства определенного интеграла
	a
1.	f (x)dx 0 .
	a
	b	a
2.	f (x)dx f (x)dx .
	a	b
		b	c	b
3.	с (a;b) :		f (x)dx	f (x)dx f (x)dx (аддитивность по интервалу).
		a	a	c

b	b	b
4.	f (x) g(x) dx	f (x)dx g(x)dx (аддитивность по функции).
a	a	a
	b	b
5. c R : cf (x)dx c f (x)dx .
	a	a
Свойства 4, 5 в совокупности называются свойством линейности опреде-
ленного интеграла.
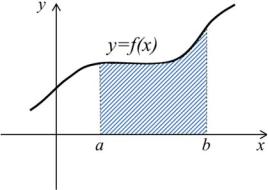
		Геометрическая		интерпретация
		(рис. 2.1). Геометрический смысл определен-
		ного интеграла (точнее, модуля определен-
		ного интеграла) – площадь фигуры, ограни-
			x a,
			x b,
		ченной кривыми	x b,
			y 0,
	Рис. 2.1.
	Рис. 2.1.	y f (x).

Этопозволяетточновычислятьплощадиплоскихфигурсосложноустроенными границами.

2.2.Методы вычисления определенного интеграла

2.2.1.Формула Ньютона–Лейбница

Пустьфункция f (x) определенаинепрерывнанаотрезке [a;b] , имеющая

первообразную F(x) , т. е.								F'(x) f (x) . В этом случае верна формула Нью-
		b									ba F (b) F (a) .
тона–Лейбница:			f (x)dx F (x)


		a
Выражение F(x)				b		мы будемназыватьдвойной подстановкой и понимать
Выражение F(x)				b		мы будемназыватьдвойной подстановкой и понимать
				a
				a
под ним	F(x)	b F(b) F(a) .
под ним	F(x)	b F(b) F(a) .
		a						3
		a

Пример 20. Вычислить x2dx .
								1
3					x	3				x		3	3	3	3		26
3						3						3	3	3	3
x2dx x2dx							c							3	1 9	1		8 2 .
x2dx x2dx							c							3	1 9	1	3	8 2 .
			3						3					3	3	3	3	3
1													1
1													1

Замечание. Среди первообразных функции f (x) можно выбрать любую.

Формула Ньютона–Лейбница сводит вычисление определенного интеграла к нахождению первообразной, с последующей двойной подстановкой. Однако определенный интеграл часто удается вычислить даже в случае, когда соответствующий неопределенный взять в элементарных функциях невозможно (невозможно применить формулу Ньютона–Лейбница), используя другие методы, рассмотрение которых остается за рамками данного пособия.

2.2.2. Замена переменной в определенном интеграле

Если функция f (x) непрерывна на отрезке [a;b] , а функции g(t), g'(t) непрерывны на отрезке [ p;q], где g( p) a, g(q) b, причем f (g(t)) определена и непрерывна на отрезке [ p; q], то можно произвести замену переменной:

b q

f (x)dx f (g(t))g'(t)dt.

a p

Замечание. В отличие от замены переменной в неопределенном интеграле, при использовании этого приема для определенного интеграла преобразованию подвергается не только подынтегральная функция, но и пределы интегрирования. В качестве альтернативы можно разбить решение на 2 этапа: сначала вычислить первообразную (используя неопределенный интеграл), а затем сделать двойную подстановку.

e ln x

Пример 21. Вычислить dx .

1 x

1-й способ: замена переменной в определенном интеграле.

			t ln x
e			1				1		2	1
e			1				1		2	1
	ln x	dx	dt	x	dx		t dt	t				1	.
		dx	dt	x	dx		t dt						.
	x					0		2			2
1	x	x 1 t ln 1				0	0			0	2
1		x 1 t ln 1					0			0
		x e t ln e 1

Обратите внимание, что при использовании замены переменной в определенном интеграле изменяются и пределы интегрирования, что позволяет получить результат, не возвращаясь к исходной переменной.

2-й способ: вычисление первообразной с последующей двойной подстановкой.

	ln x	dx	1	d (ln x) =	(ln x)2
Вычислим первообразную:						c .
	x		x		2

Теперь сделаем двойную подстановку:	(ln x)2	e	(ln e)2	(ln1)2	1	.

	2	1	2	2	2

При таком способе решения не приходится делать замену переменной в определенном интеграле (в частности, задумываться о том, как меняются пределы интегрирования). Но зато приходится выполнять замену переменной в неопределенном интеграле, в частности, после того, как первообразная найдена в терминах новой переменной, нужно не забыть вернуться к исходной, прежде чем делать двойную подстановку.

2.2.3. Интегрирование по частям

Формула интегрирования по частям для определенного интеграла аналогична соответствующей формуле для неопределенного интеграла:

b											b
u dv						uv	ba v du .


a											a
																				1
Пример 22. Вычислить x arctg(x)dx .
																				0
																																		1
1												u(x)					arctg(x) du																		dx
1												u(x)					arctg(x) du																		dx
x arctg(x)dx																																	1 x2			=
x arctg(x)dx																														x		2				=
0																					dv x dx									x
																					dv x dx										2
																															2
		x		2							1			1		1			x		2
				2							1					1					2
																								dx .

	2				arctg(x)									2					2
	2										0			2		0 x					1
																													x		2						1
																															2						1
Результаты двойной подстановки:																																	arctg(x)						.


																														2								4
1			2					1		2													1														0
																																					0
		x							x				1 1															1												1	1 .
		x				dx			x				1 1					dx							1			1				dx x arctg(x)
						dx												dx							1							dx x arctg(x)
	2 1												2 1																											0
																																								0
0 x								0			x												0				x2 1														4
Итоговый ответ:
1															1											3 4
															1											3 4
x arctg(x)dx																	1													.
x arctg(x)dx												4			2		1					4				8				.
0												4			2							4				8
0

2.3. Приложения определенного интеграла

2.3.1. Вычисление площадей

Площадь S	фигуры, ограниченной двумя	непрерывными кривыми
y f (x), y g(x)	g(x) f (x) и двумя прямыми	x a, x b (a b) , равна

S g(x) f (x) dx.

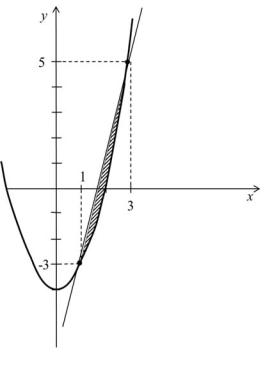
Пример 23.

Вычислить площадь фигуры, f (x) x2 4, g(x) 4x 7 (рис. 2.2).

Найдем точки пересечения заданных кривых, приравнивая их значения:

x2 4 4x 7 x2 4x 3 0

x 1,

x 3.

	На отрезке [1; 3] верно				g(x) f (x) , по-
этому искомая площадь:
	3	4x 7 (x2 4) dx
	S	4x 7 (x2 4) dx
	1
3			2x2			x	3	3
3							3	3
	(4x 3 x2 )dx			3x
	(4x 3 x2 )dx			3x
					3
1								1
1								1

18 9 9 2 3 13 113 .

ограниченной кривыми

Рис. 2.2

Пример 24.

x 3cos t,

Вычислить площадь области, ограниченной эллипсом, y 5sin t.

Вычислим площадь S1 верхней половины эллипса и потом удвоим. В этом случае получается фигура, ограниченной двумя непрерывными кривыми – эллипсом и прямой y 0 .

Получена криволинейная трапеция, площадь которой равна y dx. Сде-

												a
лаем замену переменной: x 3cost ,									dx (3cost)' dt 3sint dt . Здесь x изме-
няется от –3 до 3, следовательно, t								изменяется от до 0.
		3			0						0
S 2S1 2			y dx 2 5sin t( 3sin t dt) 30 sin 2 t dt 30 sin 2 t dt
		3										0
1 2 cos 2t			t			sin 2t				30
1 2 cos 2t			t			sin 2t				30
30		dt 30									15 .
30	2	dt 30		2		4				2	15 .
0							0
0							0

Полученный ответ соответствует формуле, утверждающей, что площадь эллипса с полуосями a и b равна ab.

2.3.2. Вычисление длин дуг

Длина дуги отрезка гладкой (непрерывно дифференцируемой) кривой

y f (x),						b	1 f '(x) 2 dx .
y f (x),			x [a;b]: l				1 f '(x) 2 dx .
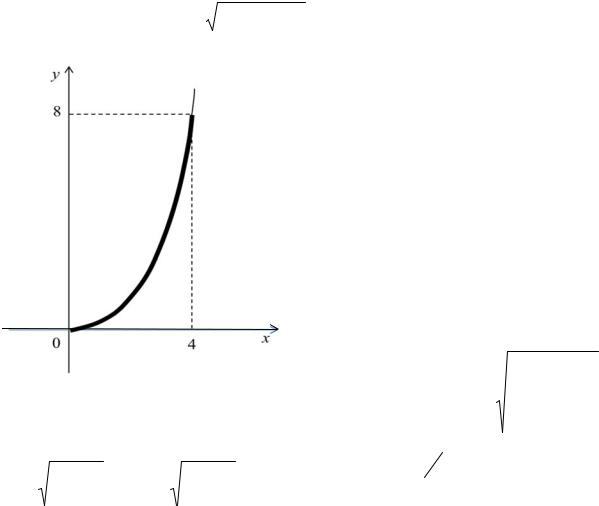
						a					Пример 25. Вычислить длину дуги


																3
																3
										кривой		f (x) x 2 , x [0;4] (рис. 2.3).
											Данная кривая является непрерывно
										дифференцируемой (гладкой) на отрезке
										[0; 4],		следовательно,									для			вычисления
										длины дуги можно применить формулу.
											Вычислим						сначала производную:
													3				1
										f '(x) (x			2 )' 3 x 2 .						Подставив резуль-
															2
										таты вычисления в формулу, получим ис-
										таты вычисления в формулу, получим ис-
																			4					3		1 2
										комую длину дуги: l														3		x 2
			Рис. 2.3							комую длину дуги: l												1		2		x 2	dx
			Рис. 2.3																1					2
																			1
4		9		4	4		9		9		8			9		3		4	8				23		3
																3		4							3
																	2								132
	1		x dx			1		x d (1		x)		1			x							10						.
	1	4	x dx	9		1	4	x d (1	4	x)	27	1		4	x							10			8			.
1		4		9	1		4		4		27			4						27					8
1					1													1
																		1

2.3.3. Вычисление объемов и площадей поверхности тел вращения

Пусть некоторое тело получено вращением криволинейной трапеции, ограниченной ветвью графика y f (x), при x [a;b], вокруг оси Ox . Объем

такого тела вращения вычисляется следующим образом: Vx f 2 (x)dx .

Поверхностью вращения называется поверхность, образованная вращением ветви графика y f (x), при x [a;b], вокруг оси Ox . Площадь поверх-

									b		1 ( f '(x))2 dx .
ности вращения вычисляется по формуле: Px 2 f (x)											1 ( f '(x))2 dx .
									a
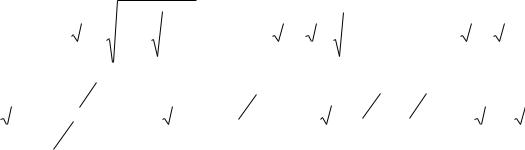
Пример26. Вычислитьобъемтелавра-
щения и площадь поверхности вращения,
полученные вращением		отрезка			прямой
y x ,	x [0;2] вокруг оси Ox (рис. 2.4).
	2		x	3	2	8 .
	2			3	2
Объем тела Vx x2dx
Объем тела Vx x2dx
	0	3			0	3
	0				0
Для данной функции найдем производ-
ную:	f '(x) x' 1. Подставив результаты
вычисления в формулу, получим искомую
площадь поверхности вращения:
											Рис. 2.4
	2	2					x	2		2	2 x2	2
	2	2						2		2
Px 2 x 1 12 dx 2 2 x dx						2 2
Px 2 x 1 12 dx 2 2 x dx						2 2
	0	0				2				0		0
						2						0

2 (4 0) 4 2 .

Пример 27. Вычислить площадь параболоида вращения, полученного вращением вокруг оси Ox дуги параболы y2 8x , x [1;4].

На данном отрезке можно рассматривать функцию y f (x) 8x .

Найдем ее производную: f '(x) (	8x)'	8	x 12	2 .
		2
				x

Вычислим площадь данного параболоида вращения:

		4								2			4							4
								2		2						x	2


	Px 2									dx	4 2		x					dx 4 2				x 2 dx

					8x 1			x								x
		1						x					1			x				1
				3		4					3	4			3				3
						4

			(x 2)	2			8						8


4	2								2 (x 2)		2			2 (6			2 3		2 ) 8		6(2 2 1) .
4	2	3					3		2 (x 2)		2		3	2 (6			2 3		2 ) 8		6(2 2 1) .
		3					3					1	3
		2				1
		2

Определенный интеграл имеет многочисленные геометрические и физические приложения, часто используемых при решении инженерных задач. В пособии рассмотрены только простейшие геометрические приложения.

Раздел «Математического анализа», посвященный интегральному исчислению функции одной переменной, является фундаментальным для математической основы инженерного образования. Существует большое число учебной литературы, содержащей этот раздел. Но их содержание зачастую много шире, последовательность изложения не соответствует необходимой для соответствующих направлений обучения. Именно поэтому краткое изложение курса, терминологии, примеры, имеющиеся в учебном пособии, помогут студентам правильно ориентироваться и в изучаемом предмете, и в учебной литературе.

СПИСОК ЛИТЕРАТУРЫ

1.Бугров Я. С., Никольский С. М. Высшая математика: учеб. для вузов: в 3 т. Т. 2: Дифференциальное и интегральное исчисление. М.: Наука, 1988; пе-

реизд.: 2003, 2006.

2.Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах: в 2 ч. М., 1986; переизд.: 2001, 2005, 2010, 2012.

3.Комплексные числа и многочлены: метод. указания к решению задач / сост.: М. Н. Абрамова, Е. А. Толкачева, А. И. Куприянов. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2007.

4.Пискунов Н. С. Дифференциальное и интегральное исчисления: в 2 т. М.: Физматлит, 1985; переизд.: 1996.

5.Сборник задач по математике для втузов: в 4 ч.: учеб. пособие для втузов: в 2 ч. / под ред. А. В. Ефимова, А. С. Поспелова. 4-е изд. М.: Физматлит,

2003.

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.02.2021909.04 Кб16Sb95700.pdf
#
13.02.2021970.61 Кб18Sb95706.pdf
#
13.02.2021869.34 Кб10Sb95738.pdf
#
13.02.2021819.27 Кб3Sb95753.pdf
#
13.02.2021730.38 Кб10Sb95858.pdf
#
13.02.2021886.23 Кб1Sb96063.pdf
#
13.02.2021817.15 Кб2Sb96070.pdf
#
13.02.2021837.57 Кб8Sb96250.pdf
#
13.02.2021790.08 Кб1Sb96262.pdf
#
13.02.2021901.25 Кб3Sb96713.pdf
#
13.02.2021804.73 Кб4Sb96714.pdf