
Sb98038
.pdf
37. В цилиндрическую цистерну с площадью основания S налита вода до |
|||||
высоты h0. В дне цистерны открыли отверстие с площадью S. Пренебре- |
|||||
гая вязкостью воды, определить, через сколько времени вся вода вытечет из |
|||||
цистерны. |
|
|
|
|
|
38. Оценить относительную погрешность вычисления периода колеба- |
|||||
ний математического маятника T 2 |
l |
g , если максимальный угол от- |
|||
клонения нити от вертикали составляет φ |
0 |
= 30○. |
|
||
|
|
|
|
|
|
39. К концам пружины жесткостью k прикреплены грузы с массами m1 = m |
|||||
и m2 = 3m. Чему равен период колебаний системы? |
|
||||
40. Брусок массой М лежит на |
|
k1 |
k2 |
||
идеально |
гладком |
горизонтальном |
|
|
M |
столе и посредством пружин, харак- |
|
|
|
||
теризуемых жесткостью k1 и k2, связан с двумя неподвижными опорами. |
|||||
1. Какова будет частота продольных колебаний бруска, если его слегка выве- |
|||||
сти из равновесного положения? Предположим, что амплитуда колебаний |
|||||
бруска равна А и в тот момент, когда он проходит положение равновесия, к |
|||||
нему прилипает упавший сверху груз массой m. Определите: 2) новую часто- |
|||||
ту колебаний, 3) новую амплитуду колебаний. |
|
||||
41. Внутри неподвижной сферической чашки радиусом R может двигаться тонкий стержень длиной l 2R, так что он остается в вертикальной
плоскости, проходящей через центр сферы. Если |
|
|
|
|
пренебречь трением, то стержень совершает неза- |
|
α |
r |
|
R |
||||
тухающие колебания. Определить их период. |
|
|
|
|
|
|
l |
|
|
42. Однородный шарик радиусом r катается без
скольжения по внутренней поверхности полусферы радиусом R, совершая малые колебания в одной вертикальной плоскости. Определить циклическую частоту этих колебаний.
43. Найти период малых колебаний половинки арбуза, лежащей на столе. Считать, что половинка арбуза представляет половину однородного шара, центр тяжести которого лежит на расстоянии 5/8 радиуса от его вершины.
11
44. Твердое тело движется в воздухе со скоростью v, превышающей среднюю скорость движения молекул воздуха. Докажите, что сила сопротивления движению тела пропорциональна квадрату скорости движения тела F = Av2, где А – площадь лобового сечения тела.
РЕШЕНИЯ ЗАДАЧ
2 |
v |
2 |
V |
L |
V |
r2 |
|
|
|
||
|
r |
||
|
2v |
|
2 |
α |
|
α |
|
1 |
Vv |
||
|
|||
11 |
r1 |
||
|
|
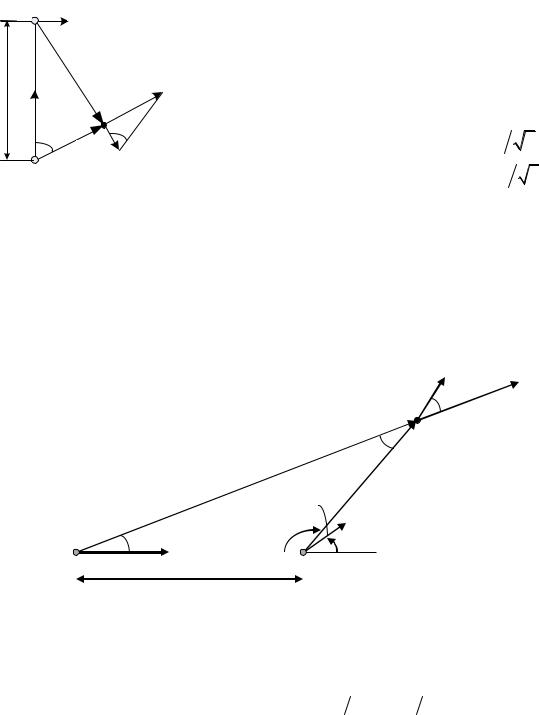
1. Жуки двигаются вокруг точки, являющейся вершиной прямоугольного треугольника, гипотенуза которого опирается в первый момент на радиус-
2Vv вектор, соединяющий жуков, длиной L. Из условия задачи и рисунка следует:
|
|
r1 |
|
|
L cos L cos arctg 2 L |
5 , |
|
|
|
|
|
||||
|
r2 |
|
Lsin Lsin arctg 2 2L |
5 . |
|||
|
|
||||||
2. В начальный момент времени ракета (точка А) и цель (точка В) находятся на расстоянии L друг от друга, а угол между векторами скоростей ракеты v1 и v2 равен α.
Пусть ракета и цель встречаются в точке О. Перемещения ракеты и цели до встречи равны r1 и r2 соответственно. Рассмотрим АОВ. Угол при вершине О равен α по условию задачи. Обозначим угол при вершине А через β.
|
|
|
О α |
v2 |
v1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
r1 |
α |
|
|
|
|
r2 |
|
|
|
|
|
|
β |
|
|
|
|
π – α – β |
v2 |
|
|
A |
β |
α |
|
|
|
|
v1 |
В |
|
|
|
|
|
L |
|
|
|
Тогда угол при вершине В будет π – α – β. Составляющие скоростей v1 и v2 на направление перемещений r1 и r2 равны v1cos и v2 cos соответственно.
Время полета ракеты |
и цели до встречи одно и |
то же. Следовательно, |
|||||||
|
r1 |
|
AO v1t cos , |
|
r2 |
|
|
OB v2t cos и OB AO v2 |
v1. По теореме косину- |
|
|
|
|
||||||
сов имеем: |
|
|
|||||||
12
L2 AO 2 OB 2 2 AO OB cos .
Отсюда для искомой величины r1 AO получаем:
|
r1 |
|
|
|
|
L |
|
|
|
|
|
|
|
||||
|
|
|
|
2 2 v |
|
|||
|
|
|
|
1 v |
v |
v cos |
||
2 |
1 |
2 |
1 |
|
||||
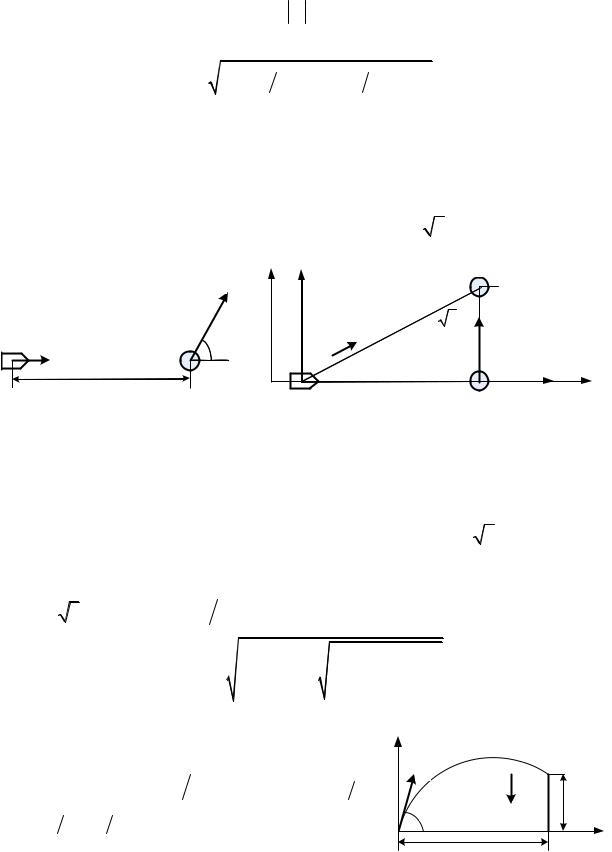
3. Нетрудно заметить, что проекции скоростей корабля и астероида на |
||||||||
ось X совпадают: для корабля vx v, |
для астероида vx 2vcos v. Поэтому |
|||||||
целесообразно рассмотреть движение тел в системе X Y , которая движется вправо со скоростью v относительно XY. В системе X Y корабль статичен, а
астероид движется вверх со скоростью vy 2vsin |
3 v. |
|
2v |
|
2v |
v |
α |
v |
|
|
L |
Y |
Y |
|
2v |
|
|
a |
S |
3 3vv |
|
|
S |
H |
|
|
|
a |
|
|
|
0 |
|
L |
X |
|
|
X |
Из корабля надо выстрелить так, чтобы поразить астероид за минимальное время t, причем по условию задачи ракета движется по прямой линии,
поэтому до столкновения с астероидом она пролетит путь S at2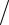 2, где a – максимальное ускорение ракеты.
2, где a – максимальное ускорение ракеты.
За то же время астероид пролетит расстояние H vy t 3 vt. По теореме Пифагора имеем H 2 L2 S2. Подставив выражения для величин Н и S, по-
лучим |
3 vt 2 L2 at2 2 . Решив уравнение относительно минимального |
||||||||||||
времени полета t, найдем t |
|
v 2 |
|
|
v 4 |
|
L 2 |
||||||
6 |
|
|
|
2 |
9 |
|
|
|
|
|
. |
||
|
|
|
|||||||||||
|
|
|
a |
|
|
a |
a |
||||||
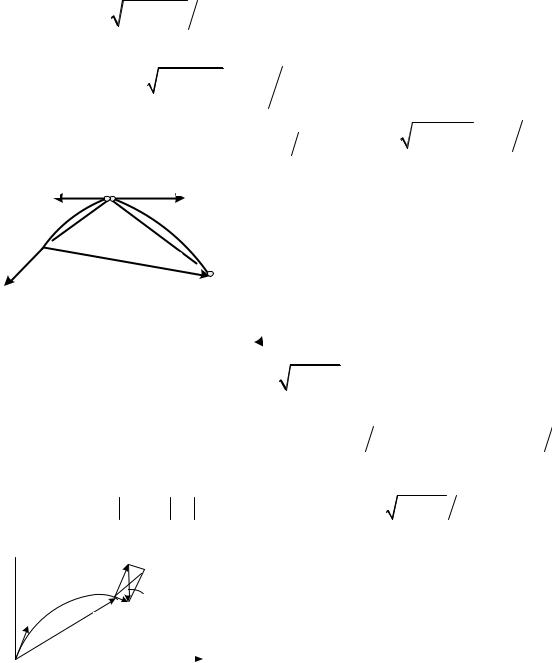
4. |
|
Составляющие |
начальной |
скорости |
y |
|
|
|||||
мяча |
v0x |
и v0y |
определяем из |
уравнений |
v0 |
|
|
|||||
x v |
|
t, |
y v |
t gt2 |
2. Откуда |
v |
L t , |
|
|
|||
|
|
|
|
|||||||||
0x |
|
0 y |
|
|
0x |
|
|
α |
g |
H |
||
v0 y H t gt 2. |
При |
этом выражение |
для |
|||||||||
00 |
|
x |
||||||||||
искомой |
величины |
принимает |
|
вид |
L |
|||||||
|
|
|
||||||||||
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
mv2 |
|
m v02x v02y |
|
m |
L2 |
H 2 |
|
g2t2 |
|
|
E |
0 |
|
|
|
|
|
|
|
|
|
. Будем считать время полета t |
|
|
|
t2 |
|
|||||||
|
2 |
|
2 |
|
2 |
|
|
|
4 |
|
|
параметром, позволяющим выделить нужную траекторию, соответствующую минимуму энергии Е, из множества парабол, удовлетворяющих условию удара под перекладину. Выделив из общего выражения для Е часть, зависящую от t2 и
полагая |
t2 = |
τ, вычислим |
dE |
|
d |
|
L2 |
H 2 |
|
g2 |
|
L2 H 2 |
|
g2 |
0 и |
||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 |
|
||||||||||
|
|
|
d |
|
d |
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
найдем |
t2 2 |
L2 H 2 g.Убедитесь самостоятельно, что найденное значе- |
|||||||||||||||
ние времени полета мяча соответствует минимуму энергии Е. Окончательно
|
L2 H 2 |
|
2 |
33,8 Дж. |
|
|
|
|
|
|
|
получим: E mg |
H |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Угол вылета мяча: arctg v0 y |
2 |
H |
2 |
H |
|
|
|||||
v0x arctg |
L |
|
|
L |
51,4 . |
||||||
v10
 r11
r11
v11
 g
g
rr2– rr1
2 1
v20
rr22 
 v2
v2
t
5. Зависимости скоростей частиц от
времени |
имеют вид |
v1 v10 gt, |
v2 v20 |
gt. По условию |
v1 v2. Сле- |
довательно, (v1 · v2) = (v10 · v20) + g2t2 = 0.
Отсюда |
находим |
момент времени, |
в который |
векторы |
скоростей частиц |
взаимно перпендикулярны: v10v20  g.
g.
Расстояние s между частицами в этот момент времени определяется мо-
дулем вектора r |
r |
,где |
r |
t v t gt2 |
2 |
и r |
t v |
t gt2 2. В ре- |
2 |
1 |
|
2 |
10 |
|
1 |
10 |
|
зультате находим
s = r2 -r1 = v20
yy vv00
vv00
 vv0 0 +v tv(t) vv00 rr(tt) v(t) ggt t
vv0 0 +v tv(t) vv00 rr(tt) v(t) ggt t
0 |
|
|
xx |
0 |
|
|
|
-v10 |
|
t =(v20 +v10 ) v10v20 |
|
g =4,1 м. |
|
||||||||
|
|
|
|||||||||||
6. |
|
При |
равноускоренном |
движении |
|||||||||
v t v |
0 |
gt, |
r t v |
t gt2 |
|
Отсюда |
|||||||
|
|
|
|
|
|
|
0 |
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
gt v t v0 и |
r t |
v |
0 |
v t |
t. |
По |
условию |
||||||
|
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
14

v t v0, |
а |
в прямоугольнике диагонали равны. Следовательно, |
|||||||
|
v t v0 |
|
gt |
и s |
|
r t |
|
gt2 |
4,9 м. |
|
|
|
|
||||||
|
|
|
|
2 |
|
||||
7. В начальный момент центр масс С системы «пробир- ка–шмель» находится на расстоянии L/4 от дна пробирки. В момент удара пробирки о стол центр масс С окажется на расстоянии 3L/4 от дна пробирки. Центр масс за время t полета пробирки переместился на расстояние L/2, двигаясь с ускорением a = g и нулевой начальной скоростью. Следова-
тельно, L 2 gt2 |
2 и t L g. |
L |
C |
|
|
|
L/4 |
|
L/4 |
g |
C |
g |
|
8. Координата y произвольной точки на |
|
yy |
|
|
|
|
|
|
|
|
|
|
|
||||||
ободе колеса может быть записана выражением |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y R 1 cos R 1 cos t R 1 cos |
|
t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
||||||
R |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vv |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
y |
|
|
|
|
|
|
|
|
|||||||
|
y vy R d sin vsin |
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Откуда |
t. |
Величины |
|
|
|
|
|
|
φ |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
dt |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
y, y и h связаны соотношением |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
h y y2 2g R 1 cos v2 sin2
2g R 1 cos v2 sin2  2g .
2g .
Максимальную высоту определим из условия |
dh |
0 |
|
cos gR |
|
||||||||
|
|
|
|
|
|
|
|
|
d |
|
|
v2 |
|
Отсюда arccos |
gR |
; |
h |
R gR2 |
|
v2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
max |
2v2 |
|
2g |
|
|
|
|
|
|
||
|
v2 |
|
|
|
|
|
|
|
|
|
|
||
Для исходных численных данных получаем 98 ; hmax 1,6 м.
9. Мячик свободно упал на землю, упруго отразился от наклонного берега и полетел по параболе. Далее последовал ряд упругих отражений, между ними участки параболических траекторий:
v t v |
n |
g t t |
n |
; |
r t r v |
n |
t t |
n |
g t t |
n |
2 |
2; t |
n |
t t |
. |
|
|
|
n |
|
|
|
|
|
n 1 |
Здесь tn – время n-го удара; vn и rn – скорость и радиус-вектор в этот момент.
Выберем систему координат: ось x вдоль склона вниз, ось y перпендикулярно склону вверх, начало координат – в точке первого удара (у ног «растяпы»). В начальный момент
15
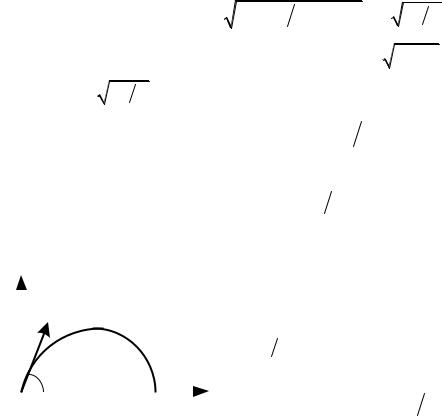
x0 = –h sin α, y0 = h cos α, v0 = 0.
Вдоль оси x мячик движется с постоянным ускорением g sin α, поэтому x t x0 gt2 sin  2.
2.
Вдоль оси y мячик движется с постоянным ускорением g cos α и упругими отражениями от склона. При отражении скорость vy меняет знак. Движение вдоль оси y аналогично обычным вертикальным прыжкам с заменой g на g cos α. Максимальная координата ymax во всех прыжках одинакова: ymax = y0. Промежутки времени между соударениями тоже одинаковы:
|
|
|
|
|
|
|
|
|
|
|
t 2 |
2 ymax |
g cos 2 2h g. |
|
|
||||||||
|
|
|
|
Первый |
удар |
произошел в момент |
t1 |
2h / g , |
момент |
n-го удара: |
|||||||||||||
tn =(2n -1) |
2h g . Координата n-го удара: |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
x x t |
n |
hsin gt2 sin |
2 4n n 1 hsin . |
|
||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Если мячик попадает в воду после n-го удара, выполняется условие |
|||||||||||||||||||
|
xn l xn 1, |
следовательно, |
n 1 n l 4hsin n n 1 . Таким образом, |
||||||||||||||||||||
n = 4 удара. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. При учете силы сопротивления воздуха |
|||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
мяч будет двигаться по баллистической траек- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
v0 |
|
|
|
|
|
|
|
|
тории. |
Исходим |
из |
уравнения |
движения: |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m dv dt mg kv, |
где kv Fc – сила сопротив- |
||||||
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ления воздуха. В проекции на ось y уравнение |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
принимает вид m dvy |
dt mg kvy.Умножим |
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
x |
|
|||||||||||
обе части уравнения на dt |
|||||||||||||||||||||||
и проинтегрируем полученное соотношение по |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 v0 sin |
|
t |
t |
|
|||
времени за |
время |
полета t: m |
|
dvy |
mg dt k vydt. Интеграл |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v0 sin |
|
|
0 |
0 |
|
||
t
vydt 0, так как он определяет перемещение мяча по вертикали, которое за
0
время полета равно нулю. В итоге получаем 1 v0 sin v0 sin gt,
откуда t 2 v0 sin  g 1,5 c.
g 1,5 c.
16
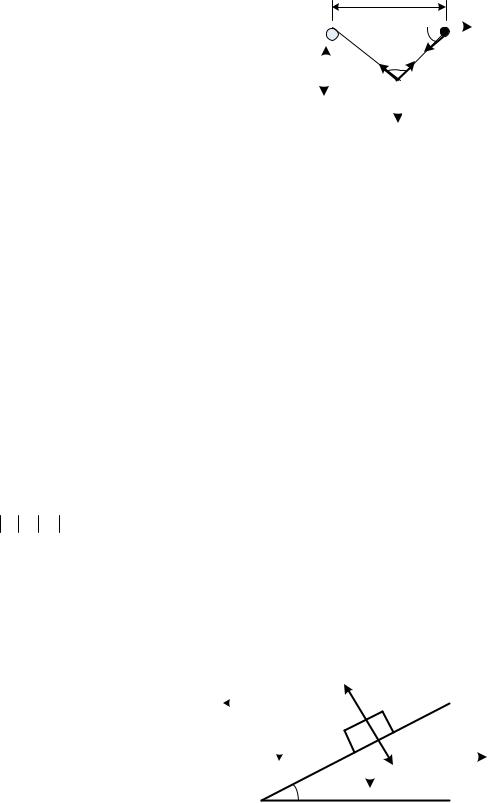
11. В точке О горизонтальная составляющая силы натяжения нити Т уравновешивается силой трения непосредственно перед началом скольжения кольца: T cos T sin . Следовательно, tg 1 4
4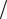 3, sin 4
3, sin 4 5, cos 3
5, cos 3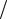 5.
5.
L
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
Fтр |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
N |
|
|
|
|
|
|
|
|
ll |
|
|
|
Fтр |
|||||||
|
|
|
|
|
|
|
|
θ |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
T |
||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
mg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mg |
|
|
|
|
|
|
Mgg |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
По теореме синусов: sin  L sin
L sin 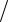 l. Отсюда ctg 0,
l. Отсюда ctg 0, 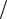 2.
2.
Векторная сумма всех сил, действующих на груз массой М = 1 кг, равна нулю (груз еще не движется!), поэтому и сумма проекций всех сил на любое направление тоже равна нулю. Спроектируем вначале все силы на направле-
ние перекинутой |
через блок |
нити, натяжение которой |
N |
N mg : |
|
N Mg cos 0, |
т. е. m M cos 0,6 кг. |
|
|
||
Аналогично, |
|
проецируя |
силы на направление нити |
l, |
находим: |
TMg sin 7,84 H.
12.Введем горизонтальную и вертикальную составляющие ускорения бруска aгор и aверт и ускорение клина a. Уравнения движения бруска и клина
ввыбранной системе координат записываются в виде
maгор N sin , maверт mg N cos ,
Ma N sin ,
где учтено, что N N . Проекции ускорений бруска и клина здесь записаны в системе отсчета, связанной с горизонтальной плоскостью; при этом направление ускорения бруска не совпадает с направлением вдоль наклонной плоскости, так как сама плоскость движется с ускорением a. Если перейти в систему отсчета, связанную с клином, то здесь ускорение клина равно нулю,
а ускорение бруска будет направлено |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
под углом β к горизонту и равно по мо- |
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
дулю aгор + a. На вертикальную проек- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
||||
цию aверт переход в новую систему от- |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
счета не окажет влияния. Таким образом, |
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|||||
|
|
|
|
|
|
|
|
|
|
mg |
|
|
|
M |
|
|
|
|||
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|||||
можно добавить еще одно необходимое |
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aверт |
tg . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
a a |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17

Решив совместно систему четырех уравнений, получим: msin 2
ag 2 M msin2
13.Гайка имеет лишь одну степень свободы, так как ее поступательное
ивращательное движение связаны. Вертикальное перемещение x при повороте на угол находим из условия x h
h 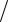 2 , дает связь соответ-
2 , дает связь соответ-
ствующих линейной v и угловой ω скоростей: v h 2 .
2 .
Здесь имеем пример задачи, в которой из закона сохранения дифференцированием можно получить уравнение движения. При отсутствии трения
закон сохранения энергии имеет вид mv2 |
2 J 2 |
2 mgx const. Отсюда |
|||||||||||||||||||||||||||||||||||||
находим выражение для квадрата скорости гайки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
v2 = |
|
2gx |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
||||
|
|
|
|
|
|
|
|
|
|
|
J 4π2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
mh2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J 4 2 1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Дифференцируя по |
|
времени, |
|
получим: |
2vv 2gx 1 |
|
|
|
|
|
|
|
|
, |
|||||||||||||||||||||||||
|
|
m |
|
|
|
||||||||||||||||||||||||||||||||||
|
J 4 2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a g 1 |
|
|
|
|
const , |
следовательно, |
работают формулы кинематики |
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
|
m h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J 4 2 |
|
|
|
v |
|
|
|
|
J 4 2 |
||||||||||||
равноускоренного |
движения: |
|
v at gt 1 |
|
|
|
|
|
, |
t |
|
|
|
|
1 |
|
|
|
|
|
|
|
. |
||||||||||||||||
m h2 |
|
g |
|
m h2 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
J 4π |
2 ö |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
÷ |
|
|
|
|
|
|
|
|
|
||||
Скорость шайбы при x = H находим по (1): v = 2gH |
|
ç |
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
ç1+ |
m h |
|
|
÷. В резуль- |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
ø |
|
|
|
|
|
|
|
|
|
||||
тате определяем t |
2H |
|
|
J 4 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
m |
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
T2
a a
m2g
 T11 a
T11 a
 m11gg
m11gg
14. Запишем второй закон Ньютона для первого и второго грузов:
m2g T2 m2a, T1 m1g m1a. |
(1) |
В уравнениях (1) учтено, что из-за трения сила натяжения Т различна для разных грузов.
Определим теперь, каким образом сила натяжения Т меняется вдоль нити. Рассмотрим элемент нити, видимый
18
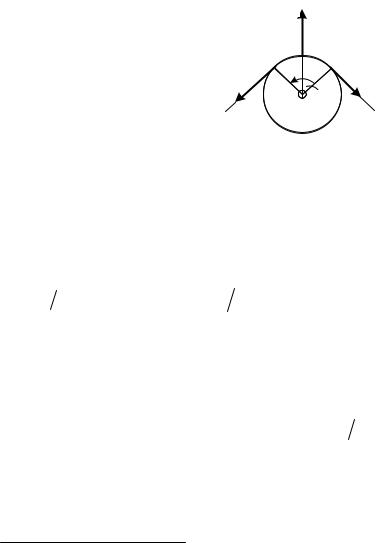
под малым углом Δα из центра блока. Силы, приложенные со стороны нити к блоку, по третьему закону Ньютона равны Т2 и Т1 соответственно. Сила реакции блока F (равная по значению силе, с которой нить прижата к блоку) равна:
|
|
F |
|
|
|
|
F |
|
|
T |
2 |
|
T |
1 |
|
|
∆α |
|
F T sin |
|
T sin |
|
1 |
T T |
1 . |
(2) |
|
|
|
|||||||
2 |
2 |
1 |
2 |
2 |
2 |
1 |
|
|
|
|
|
|
|
|
|||
Поскольку нить невесома, видно, что ее натяжение меняется из-за силы |
||||||||
трения: |
|
|
|
|
|
|
|
|
|
|
T T2 T1 F, |
|
|
||||
что вместе с (2) дает уравнение T T T T2 |
T1 2. Переходя от ко- |
|||||||
нечных приращений к бесконечно |
малым |
d , получаем |
уравнение |
|||||
dT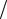 T d , решение которого есть T2
T d , решение которого есть T2 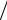 T1 exp 2 1 . Если нить про-
T1 exp 2 1 . Если нить про-
сто накинута |
на блок |
(один оборот), то следует положить 2 |
1 . |
В случае n |
оборотов: |
2 1 2 n 1 . Таким образом, |
T2 T1 |
exp 2n 1 . Подставив это соотношение в (1) и исключив Т, получим окончательно:
a g m2 m1 exp 2n 1 m2 m1 exp 2n 1
Учитывая, что a > 0, заключаем, что грузы придут в движение при усло-
вии m2 m1 exp 2n 1 , тогда как в случае m2 m1 exp 2n 1 они останутся в покое.
15. Пусть не соскользнула часть каната длиной x, тогда соскользнувшая часть каната имеет длину l – x. Обозначим массу каната буквой m.
Запишем второй закон Ньютона для всего каната и для его висящей части:
|
|
x |
|
|
x |
|
|
x |
|
|||
ma mg 1 |
|
|
|
, m 1 |
|
|
a mg 1 |
|
|
|
T. |
|
|
|
|
||||||||||
|
|
l |
|
|
l |
|
|
l |
|
|||
Отсюда |
|
|
|
|
|
T mg |
x |
|
x |
||
|
1 |
|
. |
||
|
|
||||
|
l |
|
l |
||
19

Максимум этого выражения будет при x l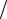 2. Тогда Tmax mg
2. Тогда Tmax mg  4. По условию задачи, чтобы канат не порвался, должно быть
4. По условию задачи, чтобы канат не порвался, должно быть
T T0 mgl0  l.
l.
Поэтому, положив Tmax mg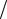 4 mgl0
4 mgl0 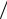 l , получим условие целостности каната:
l , получим условие целостности каната:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mg mg |
l0 |
, l |
max |
4l . |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
l |
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
16. Система отсчета, связанная с бруском и |
||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
маятником, является неинерциальной. Она дви- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жется с ускорением |
|
|
||||||||
|
|
|
β |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
a = g(sin α-μcosα) |
(1) |
|||||
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
ma |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
относительно инерциальной (земли). Второй закон |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
mg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
mg |
|
|
|
|
|
|
|
динамики при движении тела массой m в неинер- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
циальной системе отсчета, обладающей ускоре- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
нием a, следует формулировать так: F Fin mw0, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где F – |
|
|
|
|
|
|
|||||||||||||||||||
|
равнодействующая |
всех внешних |
сил, действующих |
на тело; |
|||||||||||||||||||||
Fin ma – сила инерции; w0 – ускорение тела в неинерциальной системе отсчета. Маятник относительно неинерциальной системы отсчета покоится, так что w0 = 0, и уравнение движения принимает вид mg T ma 0. Избав-
ляясь от векторов в выбранной системе координат, приходим к алгебраическим уравнениям: macos T sin 0 и T cos masin mg 0. Исключив
из них Т, получим: tg |
acos |
Подставив сюда выражение (1), после |
|
g asin |
|||
|
|
несложных преобразований окончательно получим формулу tg |
tg |
, |
||||
1 tg |
||||||
|
|
|
|
|
||
|
tg |
|
Заметим, что в отсутствие трения (μ =0) β = α. |
|
||
откуда arctg |
|
|
||||
|
|
|||||
|
1 tg |
|
|
|
||
17. В данной задаче нельзя пренебречь неинерциальностью системы отсчета, связанной с Землей. Для наблюдателя, находящегося на Земле, урав-
нение |
движения тела записывается в виде ma Fт Fцб Fк, где |
||||
F |
|
mMЗ |
|
– сила всемирного тяготения, направленная к центру Земли; |
|
R h |
2 |
||||
т |
|
|
|||
|
|
З |
|
|
|
20
