3. Оформление многостраничных документов в Word 2007 / Лабораторная_3_Вариант_2

1. Численное вычисление значений определенного интеграла

Под определенным интегралом функции f (x) на отрезке [a, b] чаще всего понимают площадь криволинейной фигуры под графиком функции f (x) (рис. 1). Предполагается, что отрезок от a до b разбит на множество маленьких интервалов величиной h, и вычислены площади i-х столбцов Si = f (xi). h, тогда можно с заданной точностью определить значение площади криволинейной трапеции, ограниченной графиком функции f (x) и равной сумме площадей элементарных интервалов.

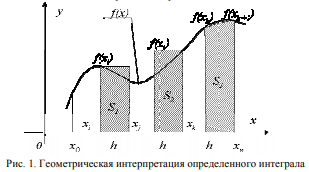
Для вычисления определенного интеграла непрерывной функции f (x) на отрезке [a, b] применяют формулу Ньютона- Лейбница

S =F (a) − F (b), (1)

где F(a), F(b) – первообразные функции от подынтегральной функции F(x) = f `(x). Однако использовать формулу (1) в большинстве случаев невозможно. Для многих функций f (x) первообразную F(x) сложно определить. Кроме того, функция f (x) может быть задана не аналитически, а таблично. В этом случае используют приближенные формулы для вычисления интеграла. Численное интегрирование широко применяется в практических расчетах, учитывая простую реализацию на компьютере и разнообразие реальных функциональных зависимостей, не описываемых элементарными функциями, заданными таблично и др. Существует несколько методов численного интегрирования. Наиболее известные из них методы прямоугольников (4), метод трапеции (6) и метод Симпсона. Сформулируем общую постановку задачи.

1. Постановка задачи

Пусть требуется вычислить

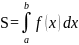(2)

на отрезке [a, b], если известно, что a и b – нижний и верхний пределы интегрирования, а функция f (x) непрерывна на интервале [a, b].

2. Метод прямоугольников

Согласно общему подходу численного интегрирования интервал [a, b] разделяют на n участков длиной

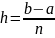. (3)

На каждом участке [xi, xi+1] заменяют подынтегральную функцию горизонтальной прямой и определяют площадь элементарного прямоугольника Si = f (xi).

Обобщенная формула для приближенного вычисления определенного интеграла методом левых прямоугольников имеет вид

(4)

Замена реальной функции f (x) уравнением прямой на участках интегрирования вносит определенную погрешность в вычисление интеграла. Погрешность будет уменьшаться при увеличении количества разбиений интервала за счет более точной аппроксимации подынтегральной функции. Очевидно, что при

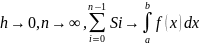. (5)

Погрешность вычисления определенного интеграла методом прямоугольников по формуле (4) пропорциональна шагу интегрирования h.

3. Метод трапеций

Более точно вычислить определенный интеграл можно с помощью метода трапеций. Подынтегральная функция f (x) разбивается на n равных участков, которые заменяются прямыми, соединяющими точки со значениями функции на границах каждого элементарного участка аппроксимации f (xk), f (xk+1). Сумма площадей образованных таким образом трапеций (рис. 1) при том же значении n точнее приближает значение интеграла к истинному, по сравнению с методами прямоугольников. Интегральная сумма метода трапеции может быть рассчитана по одной из равносильных формул:

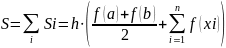
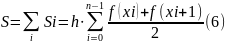
Погрешность@≠ƛ∑‰метода@≠ƛ∑‰трапеций@≠ƛ∑‰(6)@≠ƛ∑‰пропорциональна@≠ƛ∑‰h2.

– Ctrl+Num –

  Ctrl+Shift+Пробел