
Ответы на билеты по матану. 1 сем
.docx1.Множество-совокупность предметов и явлений, объединенных общим свойством.
Свойства суммы
∀a,b∈R∀a,b∈R операция a+ba+b называется суммой и обладает следующими свойствами:
1) Коммутативность сложения
∀a,b∈Ra+b=b+a∀a,b∈Ra+b=b+a
Для любых действительных чисел a и b сумма a и b равна сумме b и a.
2) Ассоциативность сложения
∀a,b,c∈R(a+b)+c=a+(b+c)∀a,b,c∈R(a+b)+c=a+(b+c)
Для любых действительных чисел a, b и c сумма a и b плюс c равна a плюс сумма b и c.
3) Свойство нуля
∀a∈R∃!0∈Ra+0=a∀a∈R∃!0∈Ra+0=a.
Для любого действительного числа a существует такое действительное число 0 и при том единственное, что сумма a и 0 равна a.
4) Свойство противоположного элемента
∀a∈R∃(−a)∈Ra+(−a)=0∀a∈R∃(−a)∈Ra+(−a)=0.
Для любого действительного числа a существует такое действительное число -a, что их сумма равна нулю.
2. Свойства умножения
∀a,b∈R∀a,b∈R операция a⋅ba⋅b называется произведением, и ей присущи следующие свойства:
1) Коммутативность умножения
∀a,b∈Ra⋅b=b⋅a∀a,b∈Ra⋅b=b⋅a.
2) Ассоциативность умножения
∀a,b,c∈Ra⋅(b⋅c)=(a⋅b)⋅c∀a,b,c∈Ra⋅(b⋅c)=(a⋅b)⋅c.
3) Свойство единицы
∀a∈R∃1∈Ra⋅1=a∀a∈R∃1∈Ra⋅1=a.
4) Свойство обратного числа
∀a∈Ra≠0∃a−1∈Ra−1=1aa⋅a−1=1∀a∈Ra≠0∃a−1∈Ra−1=1aa⋅a−1=1.
Множество R∖{0}R∖{0} относительно операции умножения является коммутативной группой.
3. Дистрибутивность умножения относительно сложения
∀a,b,c∈R(a+b)⋅c=ac+bc∀a,b,c∈R(a+b)⋅c=ac+bc.
4. Свойства отношения порядка
Для любых действительных чисел a и b: или a≤ba≤b, или a≥ba≥b. При этом выполняются следующие свойства:
1) Свойство полноты
∀a,b∈R∀a,b∈R справедливо одно из трёх: a=ba=b, a>b(b<a)a>b(b<a), a<b(b>a)a<b(b>a).
Для любых действительных чисел a и b справедливо одно из трёх утверждений: либо a и bравны, либо a больше b (b меньше a), либо a менше b (b больше a).
2) Рефлексивность
∀a∈Ra≤a∀a∈Ra≤a.
Для любого действительного числа a: a меньше либо равно a.
3) Свойство тождества
∀a,b∈Ra≤bиa≥b⇒a=b∀a,b∈Ra≤bиa≥b⇒a=b.
Если для двух любых действительных чисел a и b выполняется условие a меньше либо равно b и b меньше либо равно a, то a и b равны.
4) Транзитивность
∀a,b,c∈Ra≤bиb≤c⇒a≤c∀a,b,c∈Ra≤bиb≤c⇒a≤c.
Для любых действительных чисел a, b, c: если a меньше либо равно b и b меньше либо равно c, то a меньше либо равно c.
5) Сохранение неравенства
∀a,b,c∈Ra≤b⇒a+c≤b+c∀a,b,c∈Ra≤b⇒a+c≤b+c.
Для любых действительных чисел a, b, c, в случае выполнения неравенства a меньше либо равно b, при прибавлении к обоим частям неравенства одного и того же числа c знак неравенства остаётся прежним.
6) Правило знаков
∀a,b∈Ra≥0иb≥0⇒a⋅b≥0∀a,b∈Ra≥0иb≥0⇒a⋅b≥0.
Произведение двух любых положительных действительных чисел положительно.
14. 4. Геометрический и физический смысл производной
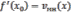 , где
, где 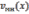 –
мгновенная скорость в момент
–
мгновенная скорость в момент 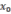 .
В этом заключается физический смысл
производной. Производная – это также
тангенс угла наклона касательной
.
В этом заключается физический смысл
производной. Производная – это также
тангенс угла наклона касательной  ,
где
,
где  -
угол наклона касательной к кривой
-
угол наклона касательной к кривой 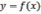 в
точке с абсциссой
.
в
точке с абсциссой
.
5. Алгоритм нахождения производной
Для того
чтобы найти 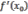 нужно:
нужно:
1) Задать
приращение 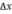 –
это приращение аргумента и вычислить
соответствующее приращение функции
–
это приращение аргумента и вычислить
соответствующее приращение функции 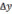 или
или 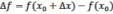 .
.
2) Найти
разностное соотношение  ,
упростить его и сократить на
.
,
упростить его и сократить на
.
3) Если
отношение
при 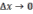 стремится
к какому-то числу, то это число будет
.
стремится
к какому-то числу, то это число будет
.
15.Теорема.
Если функция 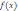 дифференцируема
в некоторой точке a, то она непрерывна
в этой точке.
Доказательство.
По определению производной
дифференцируема
в некоторой точке a, то она непрерывна
в этой точке.
Доказательство.
По определению производной
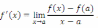
Это предельное равенство означает, что выражение под знаком предела можно представить в виде

где α(x) – бесконечно малая функция при x → a. Тогда
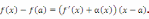
Следовательно,
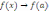 при x → a.
Заметим, что
дифференцируемость функции в некоторой
точке означает ее гладкость в окрестности
этой точки, что влечет за собой
непрерывность функции в рассматриваемой
точке. Однако обратное утверждение
несправедливо – функция, обладающая
свойством непрерывности в некоторой
точке, не обязательно дифференцируема
в этой точке.
при x → a.
Заметим, что
дифференцируемость функции в некоторой
точке означает ее гладкость в окрестности
этой точки, что влечет за собой
непрерывность функции в рассматриваемой
точке. Однако обратное утверждение
несправедливо – функция, обладающая
свойством непрерывности в некоторой
точке, не обязательно дифференцируема
в этой точке.
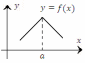 Рис.
8. Непрерывная в точке a функция
не является дифференцируемой в этой
точке.
Рис.
8. Непрерывная в точке a функция
не является дифференцируемой в этой
точке.
16. Постоянный множитель c можно выносить за знак производной:
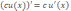
Правило 1 непосредственно вытекает из определения производной функции и свойства пределов функций, согласно которому постоянный множитель можно выносить за знак предела.

Если существуют
производные 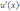 и
и 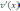 ,
то производная от суммы (разности)
функций
,
то производная от суммы (разности)
функций 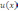 и
и 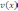 равна сумме (разности) производных:
равна сумме (разности) производных:
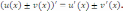
Правило дифференцирования суммы или разности функций также следует из определения производной функции и свойства пределов функций, согласно которому предел суммы (или разности) функций равен сумме (или разности) соответствующих пределов.
Если существуют производные и , то выполняются следующие правила дифференцирования произведения функций и частного от их деления:
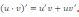
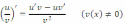
17.
18. Если y=f(x) и x=g(y) — пара взаимно обратных функций, и функция y=f(x) имеет производную f'(x), то производная обратной функции g'(x)=1/f'(x).
Таким образом, производные взаимно обратных функций — обратные величины. Формула для производной обратной функции:
Примеры. Найти производную обратной функции:
1) y=x²-7lnx.
Имеем:
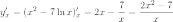
Отсюда
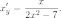
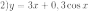
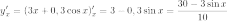
Отсюда
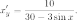
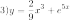
Отсюда
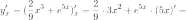
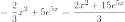
и

21. Предположим,
что функциональная зависимость  от
от  не
задана непосредственно
не
задана непосредственно 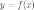 ,
а через промежуточную величину —
,
а через промежуточную величину —  .
Тогда формулы
.
Тогда формулы
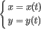
задают параметрическое представление функции одной переменной.
Пусть
функция 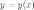 задана
в параметрической форме, то есть в виде:
задана
в параметрической форме, то есть в виде:
где
функции 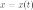 и
и 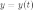 определены
и непрерывны на некотором интервале
изменения параметра
.
Найдем дифференциалы от правых и левых
частей каждого из равенств:
определены
и непрерывны на некотором интервале
изменения параметра
.
Найдем дифференциалы от правых и левых
частей каждого из равенств:
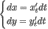
Далее,
разделив второе уравнение на первое,
и с учетом того, что 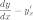 ,
получим выражение для первой производной
функции, заданной параметрически:
,
получим выражение для первой производной
функции, заданной параметрически:
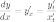
Для нахождения
второй производной 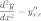 выполним
следующие преобразования:
выполним
следующие преобразования:


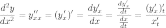
22.
23.
2 4.
4.
25.
Степенно-показательной
функцией (или показательно-степенной,
или функцией в степени функция)
называется функция вида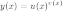
 Рассмотрим
способы нахождения ее производной.
Рассмотрим
способы нахождения ее производной.
1-ЫЙ СПОСОБ
Применяя формулу:
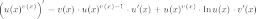
То есть вначале производная берется как от степенной функции, а потом как от показательной.
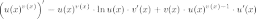
2-ОЙ СПОСОБ
С помощью логарифмического дифференцирования:
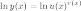
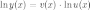
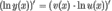

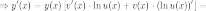
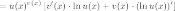
26.
27.
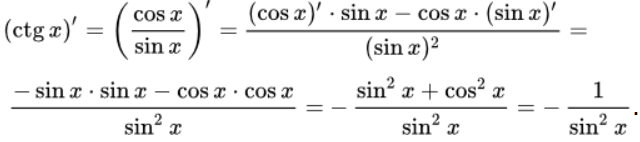
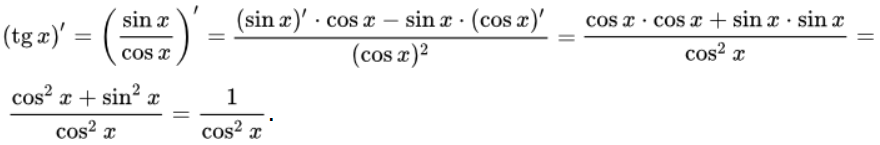

28.

29.
30. Дифференциалом
функции называется линейная
относительно  часть
приращения функции. Она обозначается
как
часть
приращения функции. Она обозначается
как 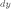 или
или 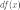 .
Таким образом:
.
Таким образом:
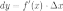
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА
Дифференциал
функции в точке  равен
приращению ординаты касательной,
проведенной к графику функции в этой
точке, соответствующему приращению
аргумента
.
равен
приращению ординаты касательной,
проведенной к графику функции в этой
точке, соответствующему приращению
аргумента
.
 Рассмотрим
дифференциал сложной функции.
Пусть y сложная функция x:
Рассмотрим
дифференциал сложной функции.
Пусть y сложная функция x:  ,
,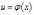 .
Дифференциал
.
Дифференциал 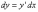 этой
функции, используя формулу для производной
сложной функции, можно записать
в виде
этой
функции, используя формулу для производной
сложной функции, можно записать
в виде 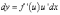 .
Но
.
Но 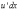 есть
дифференциал функции u, поэтому
есть
дифференциал функции u, поэтому 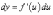 ,
т. е.
,
т. е.
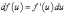 .
.
Здесь
дифференциал записан в том же виде, как
и в формуле для дифференциала функции
независимой переменной x, т. е. 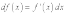 ,
хотя аргумент u является не
независимой переменной, а функцией x.
,
хотя аргумент u является не
независимой переменной, а функцией x.
Следовательно, выражение дифференциала функции в виде произведения производной этой функции на дифференциал её аргумента справедливонезависимо от того, является ли аргумент независимой переменной или функцией другой переменной. Это свойство называется инвариантностью (неизменностью)формы дифференциала.
31.
Использование дифференциалов в приближенных вычислениях |
|
Если функция y=f(x) является дифференцируемой в точке x0, то при изменении аргумента на Δx ее приращение в этой точке выражается формулой Δy=AΔx+ο(Δx), где первое слагаемое AΔx представляет собой дифференциал функции, а второе слагаемое является величиной более высокого порядка малости по отношению к Δx. Дифференциал функции обозначается символом dy и связан с производной в точке x0 соотношением dy=AΔx=f′(x0)Δx. Таким образом, приращение функции Δy можно записать как Δy=dy+ο(Δx)=f′(x0)Δx+ο(Δx). При достаточно малых приращениях аргумента Δx можно пренебречь "нелинейной" добавкой ο(Δx). В таком случае справедливо приближенное равенство Δy≈dy=f′(x0)Δx. Заметим, что абсолютная погрешность данного приближения, то есть разность Δy−dy стремится к нулю при Δx→0: limΔx→0(Δy−dy)=limΔx→0[dy+ο(Δx)−dy]=limΔx→0ο(Δx)=0. Более того, относительная погрешность также стремится к нулю при Δx→0: limΔx→0Δy−dydy=limΔx→0ο(Δx)f′(x0)Δx=1f′(x0)limΔx→0ο(Δx)Δx=0, поскольку ο(Δx) соответствует члену второго и более высокого порядка малости по отношению к Δx. Таким образом, для приближенных расчетов можно использовать следующую формулу:f(x)≈f(x0)+f′(x0)Δx,где Δx=x−x0 и Δy=f(x)−f(x0). |
32. ВЫЧИСЛЕНИЯ ПРОИЗВОДНОЙ ЛЮБОГО ПОРЯДКА, ФОРМУЛА ЛЕЙБНИЦА
Для вычисления производной любого порядка от произведения двух функций, минуя последовательное применение формулы вычисления производной от произведения двух функций, применяется формула Лейбница:
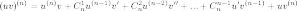
где 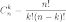 ,
, 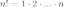 -
факториал натурального
числа
-
факториал натурального
числа  .
.
Пример
Задание. Найти 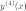 ,
если
,
если 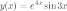
Решение. Так
как заданная функция представляет
собой произведение двух функций 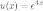 ,
, 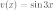 ,
то для нахождения производной четвертого
порядка целесообразно будет применить
формулу Лейбница:
,
то для нахождения производной четвертого
порядка целесообразно будет применить
формулу Лейбница:
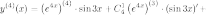
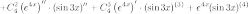
Найдем все производные и посчитаем коэффициенты при слагаемых.
1) Посчитаем коэффициенты при слагаемых:
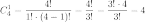
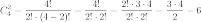
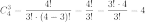
 2)
Найдем производные от функции
2)
Найдем производные от функции 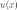 :
:
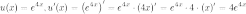
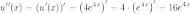
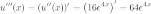
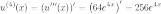
3) Найдем
производные от функции 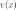 :
:
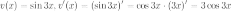
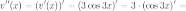
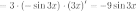
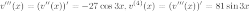
Тогда
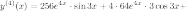
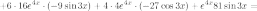
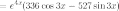
 О
О твет.
твет. 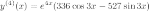
33.
Теорема Лагранжа. (О конечных приращениях)
Пусть функция
непрерывна на отрезке ;
дифференцируема
на интервале 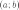 .
.
Тогда на интервале найдется по крайней мере одна точка , такая, что

Замечание
Теорема
Ролля есть частный случай теоремы
Лагранжа, когда 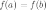 .
.
Следствие. (Геометрический смысл теоремы Лагранжа)
Н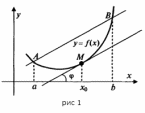 а
кривой
между
точками
а
кривой
между
точками  и
и  найдется
точка
найдется
точка  ,
такая, что через эту точку можно провести
касательную, параллельную хорде
,
такая, что через эту точку можно провести
касательную, параллельную хорде 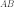 (рис.
1).
(рис.
1).
Доказанная формула называется формулой Лагранжа или формулой конечных приращений. Она может быть переписана в виде:
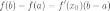
34. Теорема
(правило Лопиталя). Пусть
функции f(x) и g(x) дифференцируемы
в некоторой окрестности точки a, за
исключением, быть может, самой точки a,
и пусть 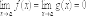 или
или 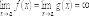 .
Тогда, если существует предел отношения
производных этих функций
.
Тогда, если существует предел отношения
производных этих функций 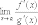 ,
то существует и предел отношения самих
функций f(x)/g(x) при x→а, причем
,
то существует и предел отношения самих
функций f(x)/g(x) при x→а, причем
|
(1) |
Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
1. Неопределенность 0/0. Первое п.Л.
Если 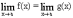 =
0, то
=
0, то 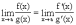 ,
если последний существует.
,
если последний существует.
2. Неопределенность вида ∞/∞ Второе п. Л.
Нахождение пределов такого типа называется раскрытием неопределенностей.
Если = ∞, то , если последний существует.
3. Неопределенности 0⋅∞, ∞- ∞, 1∞и 00 сводятся к неопределенностям 0/0 и ∞/∞ путем преобразований. Такая запись служит для краткого указания случая при отыскании предела. Каждая неопределенность раскрывается по своему. Правило Лопиталя можно применять несколько раз, пока не избавимся от неопределенности. Применение правила Лопиталя приносит пользу тогда, когда отношение производных удается преобразовать к более удобному виду легче, чем отношение функций.
0⋅∞ произведение двух функций, первая стремится к нулю, вторая к бесконечности;
∞- ∞ разность функций, стремящихся к бесконечности;
1∞ степень, ее основание стремится к единице, а показатель к бесконечности;
∞0 степень, ее основание стремится к бесконечности, а степень к нулю;
00 степень, ее основание стремится к 0 и показатель тоже стремятся к нулю.
35. Критерий возрастания и убывания функции
Снова рассмотрим функцию y=f(x), считая ее дифференцируемой на некотором интервале (a,b).Возрастание или убывание функции на интервале определяется по знаку первой производной функции. Теорема 1. Для того, чтобы функция y=f(x) была возрастающей на интервале (a,b), необходимо и достаточно, чтобы первая производная функции была неотрицательной всюду на данном интервале:f′(x)≥0∀x∈(a,b).Аналогичный критерий действует для случая функции, убывающей на интервале (a,b):f′(x)≤0∀x∈(a,b).Докажем обе части теоремы (необходимость и достаточность) для случая возрастающей функции. Необходимое условие. Рассмотрим произвольную точку x0∈(a,b). Если функция y=f(x) возрастает на (a,b), то по определению можно записать, что∀x∈(a,b):x>x0⇒f(x)>f(x0);∀x∈(a,b):x<x0⇒f(x)<f(x0).Видно, что в обоих случаях выполняется неравенствоf(x)−f(x0)x−x0≥0,гдеx≠x0.В пределе при x→x0 левая часть неравенства равна производной функции в точке x0, т.е. по свойству сохранения знака предела:limx→x0f(x)−f(x0)x−x0=f′(x0)≥0.Это соотношение справедливо для любых x0∈(a,b). Рассмотрим достаточное условие, т.е. обратное утверждение. Пусть производная f′(x) функции y=f(x) неотрицательна на интервале (a,b):f′(x0)≥0∀x∈(a,b).Если x1 и x2 − две произвольные точки данного интервала, такие, что x1<x2, то по теореме Лагранжа можно записать:f(x2)−f(x1)=f′(c)(x2−x1),где c∈[x1,x2],⇒c∈(a,b). Поскольку f′(c)≥0, то правая часть равенства неотрицательна. Следовательно,f(x2)≥f(x1).т.е. функция y=f(x) является возрастающей на интервале (a,b).
Правило нахождения экстремумов функции y=f(x) с помощью первой производной
Найти производную функции f′(x).
Найти критические точки по первой производной, т.е. точки, в которых производная обращается в нуль или терпит разрыв.
Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции f(x). Если на промежутке f′(x)<0, то на этом промежутке функция убывает; если на промежутке f′(x)>0, то на этом промежутке функция возрастает.
Если в окрестности критической точки f′(x)меняет знак с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.
Вычислить значения функции в точках минимума и максимума.
ПРИМЕР №1: Найти промежутки монотонности и экстремумы функции: f(x)=x3–3x2. Решение: Найдем первую производную функции f′(x)=3x2–6x. Найдем критические точки по первой производной, решив уравнение 3x2–6x=0; 3x(x-2)=0 ;x = 0, x = 2
Исследуем поведение первой производной в критических точках и на промежутках между ними.
x |
(-∞, 0) |
0 |
(0, 2) |
2 |
(2, +∞) |
f′(x) |
+ |
0 |
- |
0 |
+ |
f(x) |
возрастает |
max |
убывает |
min |
возрастает |
f(0) = 03 – 3*02 = 0 f(2) = 23 – 3*22 = -4 Ответ: Функция возрастает при x∈(-∞ ; 0)∪(2; +∞); функция убывает при x∈(0;2); точка минимума функции (2;-4); точка максимума функции (0;0).
36.
Точка  называется
точкой локального максимума функции
называется
точкой локального максимума функции 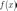 ,
если выполняется условие:
,
если выполняется условие: 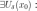
 Аналогично
точка
называется
точкой локального минимума функции
,
если выполняется условие:
Аналогично
точка
называется
точкой локального минимума функции
,
если выполняется условие:
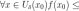
Точки, в которых производная равна нулю, называются стационарными точками. Точки, в которых функция непрерывна, а её производная либо равна нулю, либо не существует, называются критическимиточками.
Теорема (необходимое условие экстремума)
Если точка — точка экстремума функции , то она критическая.
Доказательство
По условию
точка
—
точка экстремума функции
 по
теореме Ферма производная
по
теореме Ферма производная 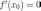 точка
является
критической.
точка
является
критической.
Теорема (первое достаточное условие экстремума в терминах первой производной)
Пусть функция определена и дифференцируема в некоторой окрестности точки , кроме, быть может, самой точки и непрерывна в этой точке. Тогда:
Если
производная  меняет
знак с «-» на «+» при переходе через
точку
:
меняет
знак с «-» на «+» при переходе через
точку
: 
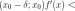
 и
и
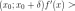 ,
то
—
точка строго минимума функции
,
то
—
точка строго минимума функции
Если
производная
меняет
знак с «+» на «-» при переходе через
точку
:
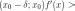 и
и
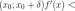 ,
то
—
точка строго максимума функции
,
то
—
точка строго максимума функции
Доказательство
Пусть,
например,
меняет
знак с «-» на «+». Рассмотрим точку
на
сегменте 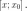 Воспользуемся
теоремой о конечных приращениях
Лагранжа:
Воспользуемся
теоремой о конечных приращениях
Лагранжа: 
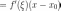 ,
, 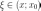 .
Поскольку при переходе через
точку
функция
меняет знак с «-» на «+», то
.
Поскольку при переходе через
точку
функция
меняет знак с «-» на «+», то 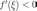 и
и 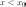 ,
то
,
то 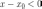
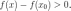 Аналогично
рассмотрим сегмент
Аналогично
рассмотрим сегмент 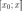 ,
получим
,
получим
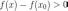
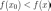 —
точка строгого минимума функции.
—
точка строгого минимума функции.
37. Определение наибольшего и наименьшего значения функции
Рассмотрим функцию y=f(x), которая является непрерывной на отрезке [a,b]. Если существует точка x0∈[a,b], такая, что для всех x∈[a,b] выполняется неравенство f(x)≤f(x0), то говорят, что функцияf(x) принимает в точке x0 наибольшее (максимальное) значение на отрезке [a,b]. Наибольшее значение функции f(x) на отрезке [a,b] является одновременно точной верхней граньюмножества значений функции на этом отрезке и обозначается какf(x0)=maxx∈[a,b]f(x)=supx∈[a,b]f(x).Аналогично, если существует точка x0∈[a,b], такая, что для всех x∈[a,b] выполняется неравенство f(x)≥f(x0), то функция f(x) принимает в точке x0 наименьшее (минимальное) значение на отрезке [a,b]. Наименьшее значение функции f(x) на отрезке [a,b] является также точной нижней гранью множества значений функции на этом отрезке и записывается в видеf(x0)=minx∈[a,b]f(x)=infx∈[a,b]f(x).Введенные понятия характеризуют поведение функции на конечном отрезке, в отличие от локального экстремума, который описывает свойства функции в малой окрестности точки. Поэтому наибольшее и наименьшее значения функции на отрезке часто называют также глобальным (абсолютным) максимумом или, соответственно, глобальным минимумом.

