4760

1

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ Г. Ф. МОРОЗОВА»

МАТЕМАТИКА (специальные разделы)

Методические указания к расчетно-графической работе

для студентов по направлению подготовки

15.03.04 – Автоматизация технологических процессов и производств

Воронеж 2018

2

УДК 517.9

Веневитина С.С. Математика (специальные разделы) [Электронный ресурс]: методические указания к расчетно-графической работе для студентов по направлению подготовки 15.03.04 – Автоматизация технологических процессов и производств / С.С. Веневитина, В.В. Зенина, И.В. Сапронов; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж, 2018. – 35 с.

Одобрено решением учебно-методического совета ФГБОУ ВО «ВГЛТУ» (протокол № 6 от 23.03.2018)

Рецензент д-р физ.-мат. наук, профессор Воронежского государственного педагогического университета В.В. Обуховский

Методические указания к выполнению расчетно-графической работы по дисциплине «Математика (специальные разделы)» предназначены для студентов ФГБОУ ВО «Воронежский государственный лесотехнический университет»,

Дисциплина «Математика (специальные разделы)» изучается в третьем семестре и включает в себя такие разделы математики как дискретная математика и операционное исчисление. Расчетно-графическая работа выполняется по теме «Дискретная математика».

В целях качественного выполнения студентами расчетно-графической работы даны необходимые рекомендации и образец выполнения этой работы. Они будут особенно полезны при самостоятельном изучении дисциплины «Математика (специальные разделы)».

Материалы данной учебно-методической разработки по содержанию, форме изложения и объѐму соответствуют задачам дисциплины и требованиям стандарта соответствующего направления подготовки.

3

1. Теоретическая часть

1.1. Основные понятия и определения

Графом G = ( X ,U ) называется совокупность двух конечных множеств:

дуг.

Последние представляют собой пары элементов u = ( xi , x j ) и изображают связи между объектами xi , x j Х в виде линий, их соединяющих. При этом связь со стрелкой называется дугой, а без стрелки – ребром.

вершиной дуги, а x j - ее конечной вершиной. Связь без стрелки (ребро) можно заменить парой противоположно направленных дуг.

Две вершины графа xi , x j называются смежными, если существует соединяющее их ребро ( xi , x j ). При этом xi , x j называют концами ребра.

Два ребра называются смежными, если они имеют общую вершину графа.

Если ребро соединяет вершины xi , x j , то говорят, что оно инцидентно

этим вершинам. При этом указанные вершины инцидентны ребру ( xi , x j ).

Вершина, для которой не существует инцидентных ей ребер, называется

изолированной.

Граф называется неориентированным (неорграфом), если каждое его ребро не ориентировано.

Граф называется ориентированным (орграфом), если каждое его ребро ориентировано.

На рис. 1 изображен неориентированный граф G = ( X ,U ):

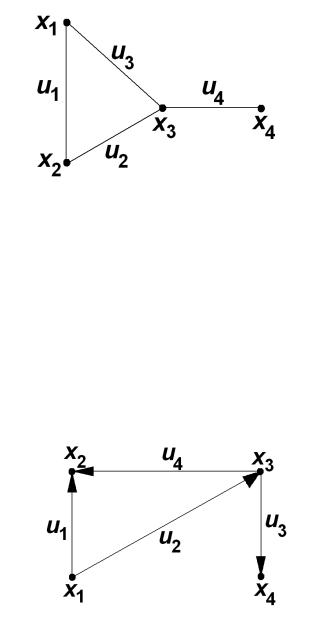
4

Х = { x1, х 2 , х3 , х 4 },

U = { u1 = ( x1, х 2 ) , u 2 = ( х 2 , х3 ), u3 = ( x1, х3 ) , u 4 = ( х 3 , х 4 ) }.

Рис. 1

На рис. 2 изображен ориентированный граф G = ( X ,U ):

Х = { x1, х 2 , х3 , х 4 },

U = { u1 = ( x1, х 2 ) , u 2 = ( x1, х3 ), u3 = ( х3 , х 4 ) , u 4 = ( х 3 , х 2 ) }.

Рис. 2

Неорграф, полученный из орграфа заменой каждой его дуги на ребро,

называется основанием графа.

Граф, у которого имеются как ориентированные ребра (дуги), так и неориентированные, называется смешанным.

Если две смежные вершины графа соединяют несколько различных ребер (при этом два ребра с совпадающими ориентациями считаются одинаковыми), то ребра называются кратными, а их количество – кратностью ребра.

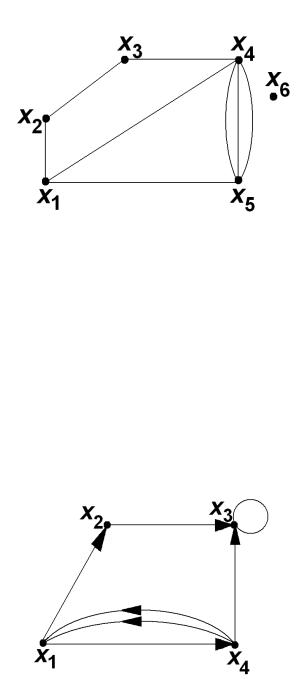
5

Если начальная и конечная вершины ребра совпадают, то ребро называют петлей (обычно ее считают неориентированным ребром).

На рис. 3 изображен неориентированный граф, у которого шесть вершин и восемь ребер. Вершина х 6 является изолированной.

На рис. 4 изображен ориентированный граф, имеющий четыре вершины и семь дуг. Смежными вершинами здесь являются, например, x1 и х 2 , х3 и х 4 .

двум (а не трем, как может показаться). Граф имеет петлю ( х3 , х3 ).

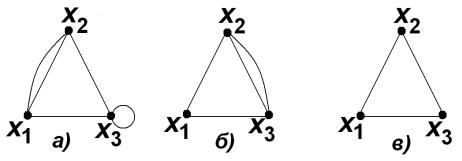
6

Граф с петлями и кратными ребрами называется псевдографом.

Граф с кратными ребрами, но без петель называется мультиграфом.

Граф без петель и кратных ребер называется простым графом.

На рис. 5 изображены: а) псевдограф; б) мультиграф; в) простой граф.

Рис. 5

Граф называется полным, если две его любые вершины – смежные, и обозначается К n , где n – число его вершин.

На рис. 3 и 4 изображены неполные графы, а на рис. 5 – все графы полные.

В случае ориентированного графа говорят, что дуга ( xi , x j ) исходит из вершины xi и заходит в вершину x j .

Число дуг, исходящих из вершины xi , называют полустепенью исхода вершины xi , которую будем обозначать d ( xi ).

Число дуг, заходящих в вершину xi , называют полустепенью захода этой вершины, которую будем обозначать d ( xi ).

Для неориентированного графа степенью вершины xi (будем обозначать ее d ( xi )) называется число ребер, инцидентных этой вершине (при этом

петли считаются дважды, а степень изолированной вершины считают равной нулю).

Для ориентированного графа степень вершины xi определяется по формуле d ( xi ) = d ( xi ) + d ( xi ).

На рис. 6 изображены: а) заданный (исходный) граф; б) остовной подграф.

Графом G = ( X , Г ) называется пара, состоящая из множества X и отображения Г. При этом множество Х называется множеством вершин графа.

Проиллюстрируем это определение на конкретном примере.

Пусть X – множество всех работ xi некоторого проекта или плана. Зададим отображение Г множества X так, что Г(xi ) - множество работ, каждая из которых не может начаться прежде, чем закончится работа xi .

Пусть, например, работами будут:

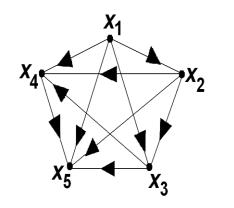
8

x1 - вспашка земли,

х2 - посев,

х3 - прополка,

х4 - уборка урожая,

х5 - доставка урожая на заготовительный пункт.

Тогда множество X запишется как X = { x1, х 2 , х3 , х 4 , х5 }, а

отображение Г можно определить следующим образом:

Г(x1) = { х 2 , х 3 , х 4 , х5 }, Г(х 2 ) = { х 3 , х 4 , х 5 }, Г(х 3 ) = { х 4 , х 5 }, Г(х 4 ) = { х 5 },

Г(х 5 ) = ø.

Множество X и отображение Г этого множества

а дуги – ( x1, х 2 ), ( x1, х3 ), ( x1, х 4 ), ( x1, х5 ),

( х 2 , х 3 ) , ( х 2 , х 4 ) , ( х 2 , х5 ) , ( х 3 , х 4 ) , ( х3 , х 5 ), ( х 4 , х 5 ). Рис. 7

1.2.Числа внутренней и внешней устойчивости графа

Пусть задан граф G = ( X , Г ).

Множество S X называется внутренне устойчивым, если никакие две вершины из S не являются смежными.

Внутренне устойчивыми множествами графа, изображенного на рис. 8,

являются, например, S1 = { x1, х3 }, S 2 = { х5 }, S 3 = { х 2 , х 4 }.

9

Множество { x1, х3 , х5 } не является

внутренне устойчивым, так как содержит смежные вершины, например, x1 и х5 .

Рис. 8

Каждое из всех внутренне устойчивых множеств S1, S 2 , S3 , … графа G

содержит определенное число | S1 | , | S 2 | , | S 3 | , … вершин этого графа.

Наибольшее из этих чисел называется числом внутренней устойчивости графа

G и обозначается символом (G) . Таким образом, по определению

G max Si .

Si X

б) содержит внутренне устойчивые множества S1= { x1, х5 }, S 2 = { x1, х3 },

S3 = { x1, х 4 }, S 4 = { х 2 , х5 }, S5 = { х 2 , х 4 }. Если к любому из них добавить еще один элемент – вершину графа, не принадлежащую множеству, - то новое подмножество вершин графа перестанет быть внутренне устойчивым. Следовательно, в этом случае (G) = 2.

Рис. 9

Пусть задан граф G = ( X , Г ).

Внешне устойчивым множеством графа называется такое подмножество

R X , что для каждого xi ( X \ R ) выполняется условие Г(xi ) R ø,

т.е. существует дуга (ребро), исходящая из xi и входящая в вершину из R.

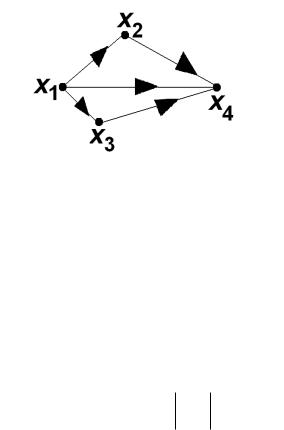
10

Внешне устойчивыми множествами графа, изображенного на рис. 10, являются, например, множества R1= { x1, х3 , х 4 } , R 2 = { x1, х 4 }, R3 = { х 4 }. Множество N = { x1, х3 } не является внешне устойчивым, так

как для вершины графа х 2 дуга, исходящая из нее, не заходит в N.

Рис. 10

Каждое из всех внешне устойчивых множеств R1, R 2 , R3 , … графа G

содержит определенное число | R1 | , | R 2 | , | R 3 | , … вершин этого графа.

Наименьшее из этих чисел называется числом внешней устойчивости графа G и обозначается символом (G) . Таким образом, по определению

G min Ri .

Ri X

Число внешней устойчивости графа, изображенного на рис. 10, равно единице, так как можно выбрать одну вершину - х 4 , в которую из оставшихся вершин

графа заходят хотя бы по одной дуге.

1. 3. Путь, цепь, контур, цикл. Связность графа

Путем в орграфе называется такая последовательность его дуг, в которой конец каждой предыдущей дуги совпадает с началом следующей. Для неорграфа такая последовательность его ребер называется цепью.

Под длиной пути (цепи) понимается количество дуг (ребер), его (ее) составляющих.

Если каждой дуге (ребру) приписано некоторое число, называемое весом, то граф называется взвешенным.