
4681
.pdf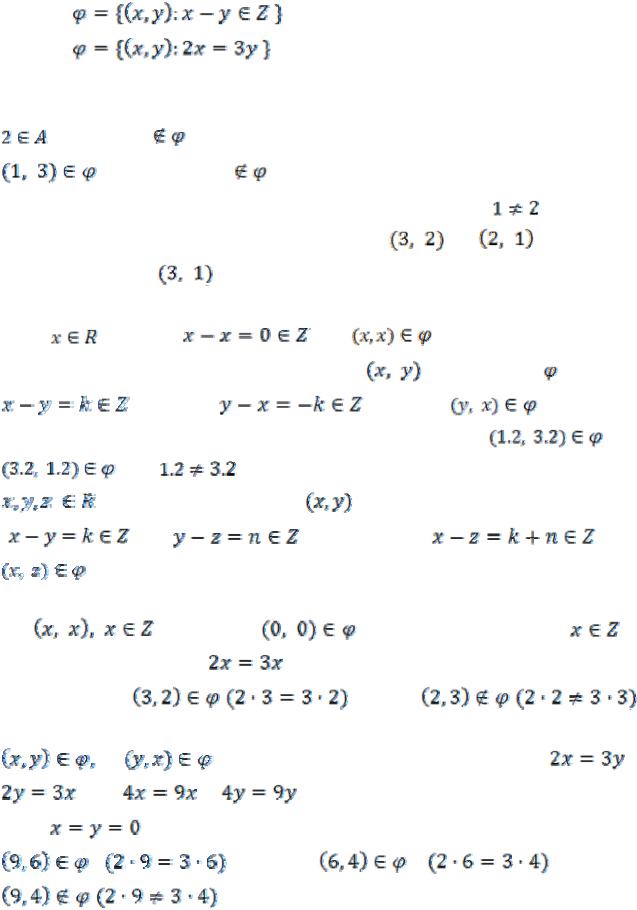
|
11 |
2) |
на множестве R; |
3) |
на множестве Z. |
Решение. |
|
1)Данное отношение не является рефлексивным, поскольку для точки
пара (2, 2) |
; не является симметричным, поскольку, например, пара |
|||||||||
|
, а пара (3, 1) |
; не является антисимметричным, |
поскольку, |
|||||||
например, пары (1, 2) и (2, 1) принадлежат отношению, но |
; не является |
|||||||||
транзитивным, поскольку, например, |
пары |
и |
принадлежат |
|||||||
отношению, а пара |
не принадлежит. |
|
|
|
|
|
||||
2) |
Данное отношение является рефлексивным, поскольку для любой |
|||||||||
точки |
разность |
|
|
, т.е. |
; является симметричным, |
|||||
поскольку |
принадлежность |
любой |
пары |
отношению |
|
означает |
||||
|
, но тогда |
|
|
, т.е. |
пара |
; |
не является |
|||
антисимметричным, |
поскольку, |
например, |
пары |
|
|
|
и |
|||
|
, но |
|
; является транзитивным, поскольку для любых |
|||||||
|
принадлежность пар |
|
и |
(y, z) отношению |
означает |
|||||
|
и |
|
|
, |
но тогда |
|
|
|
, |
т.е. |
. |
|
|
|
|
|
|
|
|
|
|
3) |
Данное отношение не является рефлексивным, поскольку из всех |
|||||||||
пар |
только пара |
|
, ведь для всех остальных |
|
не |
|||||
выполнено |
равенство |
|
; |
не |
является |
симметричным, |
поскольку, |
|||
например, |
пара |
|
|
|
, а пара |
|
|
|
; |
|
является |
антисимметричным, |
поскольку |
для |
любых |
пар |
|||||
|
|
одновременно выполняются равенства |
|
|
и |
|||||
, |
т.е. |
и |
|
, но это может быть только в том случае, |
||||||
если |
; не |
является транзитивным, |
поскольку, |
например, |
пара |
|||||
|
|
, |
пара |
|
|
|
|
, |
но |
пара |
|
|
. |
|
|
|
|
|
|
|
|

12
1.5 Отображение множеств
Пусть M и N – два произвольных множества. Говорят, что на M определена функция f, принимающая значения из N, если каждому элементу 

 M поставлен в соответствие один и только один элемент
M поставлен в соответствие один и только один элемент  N. В случае
N. В случае
множеств произвольной природы вместо термина «функция» часто пользуются термином «отображение», говоря об отображении одного множества в другое.
Если a – элемент из M, то соответствующий ему элемент b=f(a) из N называется образом элемента a. Совокупность всех элементов из M, образом которых является данный элемент b
 N, называется прообразом элемента b и
N, называется прообразом элемента b и
обозначается (b).
(b).
Пусть А – некоторое подмножество из M; совокупность {f(a):a A} всех элементов вида f(a), где a
A} всех элементов вида f(a), где a
 А, называется образом подмножества А и
А, называется образом подмножества А и
обозначается f(А). В свою очередь для каждого подмножества B из N определяется его прообраз подмножества  (B), а именно:
(B), а именно:  (B) есть совокупность элементов из M, образы которых принадлежат B. Может оказаться, что ни один элемент b из B не имеет прообраза, тогда полный прообраз
(B) есть совокупность элементов из M, образы которых принадлежат B. Может оказаться, что ни один элемент b из B не имеет прообраза, тогда полный прообраз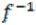 (B) будет пустым множеством.
(B) будет пустым множеством.
Установим основные свойства отображений.
Теорема 1. Прообраз суммы двух множеств равен сумме их прообразов:


 (A
(A
 B)=
B)= 


 (A)
(A)  (B).
(B).
Теорема 2. Прообраз пересечения двух множеств равен пересечению их прообразов:
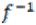 (A
(A

 B)=
B)=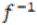 (A)
(A) 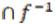 (B).
(B).
Теорема 3. Образ суммы двух множеств равен сумме их образов:
f(A
 B)=
B)=  (A)
(A) 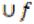 (B).
(B).
Заметим, что образ пересечения двух множеств, вообще говоря, не совпадает с пересечением их образов.

13
2.ЧИСЛОВЫЕ МНОЖЕСТВА
2.1Свойства действительных чисел
Операция сложения.
Для любых двух чисел a и b определено единственным способом число, называемое их суммой и обозначаемое a + b. Сумма обладает свойствами:
1.Для любых a и b выполняется a + b= b + a. Это свойство называется переместительным (коммутативным) законом сложения.
2.Для любых a, b, с выполняется a + (b + с)= (a + b)+c. Это свойство называется сочетательным (ассоциативным) законом сложения.
3.Существует число 0, называемое нулем, такое, что для любого числа a выполняется a + 0= a.
4.Для любого a существует число, обозначаемое -a и называемое противоположным данному, такое, что a +(-a)=0.
Далее вместо a +(-b) будем писать a - b.
Операция умножения.
Для любых двух чисел a и b определено единственным способом число,
называемое их произведением и обозначаемое |
a b. Произведение обладает |
|
свойствами: |
|
|
5. |
Для любых a и b выполняется a b= b a. Это свойство называется |
|
|
переместительным (коммутативным) законом умножения. |
|
6. |
Для любых a, b, с выполняется a (b |
с)= (a b) c. Это свойство |
|
называется сочетательным (ассоциативным) законом умножения. |
|
7. |
Существует число 1, называемое единицей, такое, что для любого |
|
|
числа a выполняется a 1= a. |
|
8.Для любого a 0 существует число, обозначаемое
0 существует число, обозначаемое 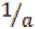 и называемое обратным данному, такое, что a
и называемое обратным данному, такое, что a 
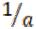 =1.
=1.

14 |
|
Связь операции сложения и умножения |
|
9. Для любых a, b, с выполняется (a + b) с = a |
c + b c. Это |
свойство называется распределительным (дистрибутивным) законом |
|
умножения относительно сложения. |
|
Упорядоченность. |
|
Для любых двух чисел a и b определено одно из соотношений a < b (a |
|
меньше b), a = b (a равно b), a > b (a больше b) так, |
что выполняются |
свойства: |
|
|
|
|
|
10. |
Если a > b , то для любого свыполняется a + c > b + c. |
|
|||
11. |
Если a > b, то для любого с > 0 выполняется a |
c > b |
c. |
|
|
Свойство непрерывности. |
|
|
|
|
|
12. |
Каковы бы ни были непустые множества |
|
у которых |
||
для любых элементов a A, |
b B выполняется неравенство a |
то |
|||
существует такое число z, |
что для всех x A, |
y B |
выполняется |
||
x |
. |
|
|
|
|
2.2 Числовые промежутки
Отрезок, интервал, полуинтервал записываются соответственно как
[a,b]={x : a 

 x
x 

 b}, (a,b)={x : a
b}, (a,b)={x : a 

 x
x 

 b}, [a,b)={x : a
b}, [a,b)={x : a 

 x < b}, (a,b]={x : a
x < b}, (a,b]={x : a 

 x
x b}.
b}.
Бесконечные промежутки записываются: |
|
||
(a, +∞)={x :x > a}, |
(-∞,a) = {x :x < a}, |
(-∞,+∞)={x :x R}. |
|
Интервал (а – а |
), где |
, называют |
– окрестностью точки а |
и обозначают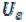 (а).
(а).

15
2.3.Точные грани числовых множеств
Множество X действительных чисел ( |
) называется ограниченным |
||
сверху, если существует число c |
такое, что все элементы множества X не |
||
превосходят c, т.е. |
|
|
|
Множество |
называется ограниченным снизу, если существует |
||
число d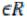 такое, что все элементы множества X не меньше d, т.е.
такое, что все элементы множества X не меньше d, т.е.
Множество 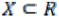 называется ограниченным, если оно ограничено как сверху, так и снизу, т.е.
называется ограниченным, если оно ограничено как сверху, так и снизу, т.е.
Последнее условие равносильно условию
Если множество 
 ограничено сверху, то наименьшее из чисел, ограничивающее его сверху, называют его точной верхней гранью или супремумом (supremum).
ограничено сверху, то наименьшее из чисел, ограничивающее его сверху, называют его точной верхней гранью или супремумом (supremum).
Число a |
является точной верхней гранью множества , если |
выполняются следующие условия: |
|
1) |
а; |
2) |
a – . |
Точная верхняя грань множества обозначается sup X.
Если множество ограничено снизу, то наибольшее из чисел, ограничивающее его снизу, называют его точной нижней гранью или инфинумом (infinum).
Число b |
является точной нижней гранью множества , если |
выполняются следующие условия: |
|
1) |
b; |
2) |
b + . |
Точная нижняя грань множества обозначается inf X.

16
Всякое ограниченное сверху (снизу) непустое множество действительных чисел имеет точную верхнюю (нижнюю) грань.
Если множество не ограничено сверху (снизу), то пишут sup X = +∞
(соответственно inf X =- ∞). |
|
Пример 1. Доказать, что множество X= {1, |
} |
ограничено. Установить, какие числа являются его гранями. Найти точные верхнюю и нижнюю грани этого множества.
|
Решение. При любом натуральном n |
выполняются неравенства |
0< |
, поэтому множество X ограничено. |
|
Докажем, что число 1 является точной верхней гранью множества X, т.е. что sup X =1. Для этого, согласно свойству точной верхней грани, надо
показать , что |
для любого |
существует |
n такое, что выполняется |
неравенство |
. |
|
|
Очевидно, |
что при n=1 выполняется |
, а это и доказывает |
|
утверждение - sup X =1.
Докажем теперь, что число 0 является точной нижней гранью
множества X. Для этого надо проверить, что для любого |
существует n |
такое, что выполняется неравенство |
|
. |
(1) |
Действительно, решая неравенство (1), получаем |
. Взяв какое- |
нибудь натуральное число 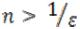 , получим требуемое n, а это, согласно
, получим требуемое n, а это, согласно
определению точной нижней грани, и означает, что inf X =0.
Отметим, что данному множеству X точная верхняя грань 1 принадлежит и является его наибольшим числом, а точная нижняя грань 0 не принадлежит множеству X и в этом множестве нет наименьшего числа.

17
3. МЕРА ПЛОСКОГО МНОЖЕСТВА
Рассмотрим систему Ω множеств на плоскости (x, y), каждое из которых определяется одним из неравенств вида
a
 x
x
иодним из неравенств вида
c

 y
y 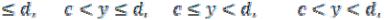
где a, b, c, d – произвольные числа. Множества, принадлежащие этой системе,
мы будем называть прямоугольниками.
Для каждого из прямоугольников определим его меру m(P), в соответствии с понятием площади, следующим образом:
а) мера пустого множества равна нулю;
б) мера непустого множества равна (b - a)(d – c). При этом выполнены следующие условия:
1)мера m(P) принимает действительные неотрицательные значения;
2)мера аддитивна, т.е. если P = 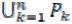 и
и 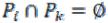 при i
при i , то
, то
m(P)=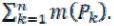
Назовем плоское множество элементарным, если его можно представить как объединение конечного числа попарно непересекающихся прямоугольников.
Теорема 1. Объединение, пересечение и разность двух элементарных множеств также являются элементарными множествами.
Определим меру m(A) для элементарного множества следующим образом: если A=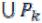 , где
, где 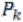 - попарно непересекающиеся прямоугольники, то
- попарно непересекающиеся прямоугольники, то
m(A)= |
. |
|
Теорема 2. Если A - элементарное множество и { |
} – конечная или |
|
счетная система элементарных множеств такая, что A |
, то |
|
m(A)=
Значения меры могут быть как конечными, так и бесконечными. Определим две функции 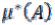 и
и 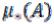 следующим образом.
следующим образом.
|
18 |
Верхней мерой |
множества A называется число |
|
, |
где нижняя грань берется по всевозможным покрытиям множества A конечными или счетными системами прямоугольников.
Нижней мерой |
множества A называется число |
|
|
|
, |
где верхняя грань берется по всевозможным |
конечным или счетным системам |
|
прямоугольников, вложенным в множество A. |
||
Множество A |
называется измеримым (в смысле Лебега), если |
|
. |
Общее значение |
верхней и нижней мер для |
измеримого множества A называется его лебеговской мерой.
4. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
Линейным пространством называется множество 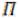 , в котором
, в котором
определены операции сложения элементов и умножения элемента на число, удовлетворяющие следующим условиям:
I) Для любых двух элементов x, y |
однозначно определен третий |
|
элемент z |
, называемый их суммой |
и обозначаемый x+y, причем |
выполняется
1)x+y=y+x (коммутативность);
2)x+(y+z)= (x+y)+z (ассоциативность);
3)в 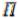 существует нулевой элемент 0 такой, что x+0=0 для всех x
существует нулевой элемент 0 такой, что x+0=0 для всех x  ;
;
4)для любого x  существует противоположный элемент -x
существует противоположный элемент -x 
такой, что x+(-x)=0 (существование противоположного элемента);
II) для любого числа a и любого элемента x |
определен элемент |
|
ax |
(произведение элемента x на число a), причем |
|
1) |
; |
|
19
2) 1 ;
;
III) Операции сложения и умножения связаны между собой дистрибутивными законами:
1) 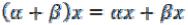 ;
;
2) 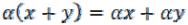 .
.
Пример 1. Прямая линия, т.е. совокупность действительных чисел, с обычными арифметическими операциями сложения и умножения, представляет собой линейное пространство.
Пример 2. n–мерное векторное пространство, т.е. совокупность всевозможных систем n действительных чисел x=( где сложение и умножение на число определяются формулами
где сложение и умножение на число определяются формулами
( |
|
( |
( |
также является линейным пространством. Оно называется n-мерным арифметическим пространством и обозначается символом 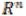 .
.
Пример 3. Непрерывные действительные функции на некотором отрезке [a, b] с обычными операциями сложения функций и умножения их на число
образуют линейное пространство |
. |
|
Элементы x, y,…, w линейного |
пространства |
называются линейно |
зависимыми, если существуют различные числа |
, не все равные |
|
нулю, такие, что |
|
|
|
|
(2) |
В противном случае данные элементы называются линейно |
||
независимыми. Иначе говоря, элементы |
x, y,…, w линейно независимы, если |
|
из равенства (2) вытекает, что |
|
|
|
= 0. |
|
Бесконечная система элементов x, y,…, w,… пространства называется линейно независимой, если любая её конечная подсистема линейно независима.
называется линейно независимой, если любая её конечная подсистема линейно независима.
Если в пространстве можно найти n линейно независимых элементов, а
можно найти n линейно независимых элементов, а
любые n+1 элементов этого пространства линейно зависимы, то говорят, что
20
пространство 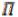 имеет размерность n. Если же в
имеет размерность n. Если же в 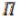 можно указать систему из произвольного конечного числа линейно независимых элементов, то говорят,
можно указать систему из произвольного конечного числа линейно независимых элементов, то говорят,
что пространство |
бесконечномерно. |
|
|
|
Базисом в |
n-мерном пространстве называется |
любая |
система из |
n |
линейно независимых элементов. Пространство |
имеет |
размерность |
n, |
|
оправдывая тем самым свое название. |
|
|
|
|
Пример 4. Одним из базисов в пространстве |
является система |
|||
векторов |
|
|
|
|
…………………..
5. ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ
Числовую функцию f, определенную на некотором линейном пространстве  , мы будем называть функционалом. Функционал f называется аддитивным, если
, мы будем называть функционалом. Функционал f называется аддитивным, если
f (x+y)= f (x) + f (y) для всех x, y 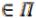 ;
;
он называется однородным , если
|
f ( |
= |
|
( число). |
Пример 1. Пусть |
- n -мерное арифметическое пространство с |
|||
элементами |
x=( |
и |
a=( |
- фиксированный |
элемент из |
. Тогда |
|
|
|
f(x)=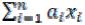
- линейный функционал в  . Пример 2. Интеграл
. Пример 2. Интеграл
I(x)=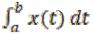
представляет собой линейный функционал в пространстве 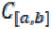 .
.
