
4621
.pdf11
К стандартным образцам предъявляется ряд требований. Наиболее важными из них являются следующие требования:
1.содержание эталонированных элементов не должно отличаться от истинного;
2.состав стандартного образца по некоторым компонентам удостоверяется официальным свидетельством (паспортом);
3.при хранении в течение длительного времени состав стандартного образца не должен меняться, он должен обладать высокой однородностью химического состава по всей массе, чтобы обеспечивать тождественность отбора проб для анализа, поэтому обычно его изготовляют в виде монолитного образца, мелкой металлической стружки, порошка и т.д.;
4.содержание эталонируемых элементов в стандартных образцах устанавливают с точностью, заведомо превышающей точность определения этих элементов в производственных образцах;
5.идеальные эталоны должны отличаться от проб лишь содержанием определяемого компонента; это практически невыполнимо, поэтому обычно ограничиваются требованием, чтобы колебания в составе проб и эталонов не вызывали систематических погрешностей, превышающих случайные.
Содержание определяемых компонентов в стандартном образце (паспортные данные) устанавливают по результатам анализов, которые проводят аналитики высшей квалификации в нескольких высокоавторитетных лабораториях с использованием различных методов.
Надежные эталоны имеются для различных групп сплавов черных и цветных металлов. Значительно сложнее изготовление эталонов для анализа руд, минералов, горных пород и т.д. в связи с разнообразием состава этих материалов.
2. Случайные погрешности
Случайные погрешности не имеют определенного знака, и само название «случайные» указывает на отсутствие какой-либо закономерности в появлении погрешности этого типа. Существование случайных погрешностей проявляется, например, в том, что результаты параллельных анализов почти всегда несколько отличаются один от другого, даже если все источники систематических погрешностей учтены с помощью соответствующих поправок. Появление случайных погрешностей обычно рассматривают как случайное событие, и эти погрешности подвергают обработке на основе теории вероятности и математической статистики.
3. Правильность, воспроизводимость и точность анализа, среднее значение и стандартное отклонение
Правильностью измерений называют качество измерений, отражающее близость к нулю систематических погрешностей.
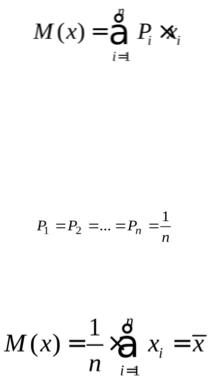
12
Повторяемостью (сходимостью) измерений называют качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в одинаковых условиях.
Более широкий смысл вкладывается в понятие «воспроизводимость».
Воспроизводимостью измерений называют качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в различных условиях (в разное время, разными методами и т.д.).
Точностью измерений называют качество измерений, отражающее близость их результатов к истинному значению измеряемой величины.
Высокая точность измерений соответствует малым погрешностям всех видов как систематическим, так и случайным. Количественно точность может быть выражена обратной величиной модуля относительной погрешности. Если, например, относительная погрешность измерения характеризуется значением 0,01 %, то точность будет равна 1/10-4 = 104.
Результат анализа, приближающийся к истинному содержанию компонента настолько, что может быть использован вместо него, следует назы-
вать действительным содержанием.
Из математической статистики известно, что наиболее вероятным и наилучшим значением измеряемой величины является математическое ожидание. Для серии из n дискретных измерений математическое ожидание М(х) определяется формулой:
(1)
где хi – результат i-гo измерения; Pi – его вероятность.
В случае равноточных измерений:
и предыдущее соотношение принимает вид:

13
Таким образом, в случае равноточных измерений математическое ожидание сов-
падает с понятием среднего арифметического.
Одним из важных свойств средней арифметической величины является то, что сумма квадратов отклонений значений Х от их средней арифметической х меньше суммы квадратов отклонений их от любой другой величины, то есть:
Положение о совпадении среднего арифметического с математическим ожиданием строго относится к гипотетической генеральной совокупности, т.е. совокупности всех наблюдений, мыслимых при данных условиях. Арифметическое среднее этих наблюдений называютгенеральным средним. В аналитической химии число параллельных определений обычно невелико и совокупность полученных резуль-
татов называют выборочной совокупностью или случайной выборкой, а среднее значение результатов случайной выборки – выборочным среднимв отличие от генерального.
Известно, однако, что при изменении числа измерений n в случайной выборке среднее арифметическое может измениться. Это ни в коей мере не уменьшает значения среднего арифметического как наиболее вероятного результата, поскольку в каждой выборке, т.е. при разных n, среднее арифметическое колеблется около своего математического ожидания. Вполне понятно, что чем больше объем выборки, тем ближе среднее арифметическое к математическому ожиданию.
Методами статистического анализа можно по результатам случайной выборки оценить параметры генеральной совокупности и таким образом найти наиболее вероятное значение содержания компонента в пробе.
Если х1,х2,...,хn – результаты параллельных определений компонента в пробе одним и тем
же методом, то среднее арифметическое будет равно:
(2)
Например, в четырех параллельных определениях олова в бронзе фотометрическим методом в виде тиомочевинного комплекса были получены следующие результаты (ωSn, %): 4,80; 4,65; 4,84; 4,61. Средним арифметическим будет значение:
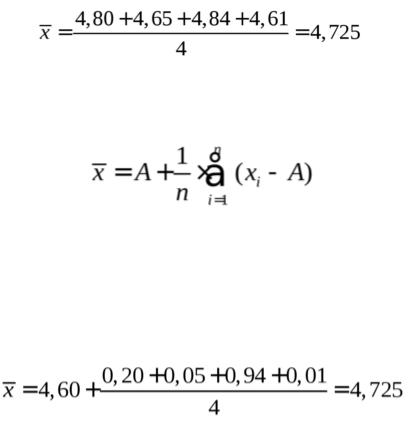
14
Для упрощения и удобства расчетов начало отсчета обычно смещают на некоторое разумно выбранное значение и вычисления проводят по формуле:
(3)
где А – произвольно выбранное значение, на которое смещается начало отсчета.
В данном случае принимаем А=4,60 и рассчитываем :
Среднее геометрическое ниже среднего арифметического.
В среднем значении, как видно, приведена одна «лишняя» значащая цифра по сравнению с исходными данными. Это сделано для того, чтобы не вносить погрешности за счет округления при проведении последующих расчетов с использованием среднего значения. Однако не следует приводить и слишком много «лишних» цифр (3-4 и более), так как это вызывает дополнительные затраты времени на вычисления, не улучшая реальной точности результата. Нередко студенты автоматически записывают полностью все число, которое «выдает» компьютер или микрокалькулятор в результате расчета, что является, конечно, неприемлемым, поскольку не характеризует достигнутую точность. Таким образом, во всех промежуточных вычислениях, включая расчет среднего арифметического, следует приводить на одну значащую цифру больше, чем число знаков в исходных данных.
Округляется только окончательный результат. Округление производится по специальным правилам и с учетом погрешности.
Отдельные результаты анализа х1, х2,…,xi рассеяны в некотором интервале значений от xmin до xmax, называемом размахом варьирования (R).Разность между отдельным результатом и средним значением называют случайным отклонением или единичным отклонением или просто отклонением (d):
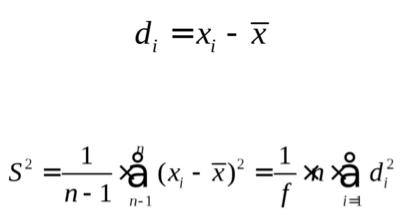
15
Рассеяние случайной величины относительно среднего значения характеризует-
ся дисперсией (S2):
(4)
где f=n-1 – число степеней свободы, определяемое как число независимых измерений за вычетом числа связей, наложенных на эту систему при обработке материала.
При вычислении дисперсии по уравнению (1) используют n независимых результатов и одну связь (2), наложенную при расчете среднего значения, поэтому число степеней свободы равно n-1. Если бы, например, генеральное среднее μ было заранее известно, то число степеней свободы при определении дисперсии было бы просто равно числу измерений, поскольку наложения связи (2) не было бы.
Если число наблюдений очень велико, величина S2 стремится к некоторому постоянному значению σ2, которое можно назватьстатистическим пределом S2. Строго говоря, этот предел и следует называть дисперсией измерений, а величи-
на S2 является выборочнойдисперсией измерений.
Одно из важнейших свойств дисперсии, имеющее большое значение в теории погрешностей, передается уравнением:
S2(х + у) = S2(х) + S2(у)
(5)
То есть дисперсия суммы случайных величин равна сумме их дисперсий. Это означает, например, что при расчете погрешности суммы случайных величин следует оперировать непосредственно с их дисперсиями.
Однако дисперсия в явном виде не может быть использована для количественной характеристики рассеяния результатов, поскольку ее размерность не совпадает с размерностью результата анализа. Для характеристики рассеяния использу-
ют стандартное отклонение (S):
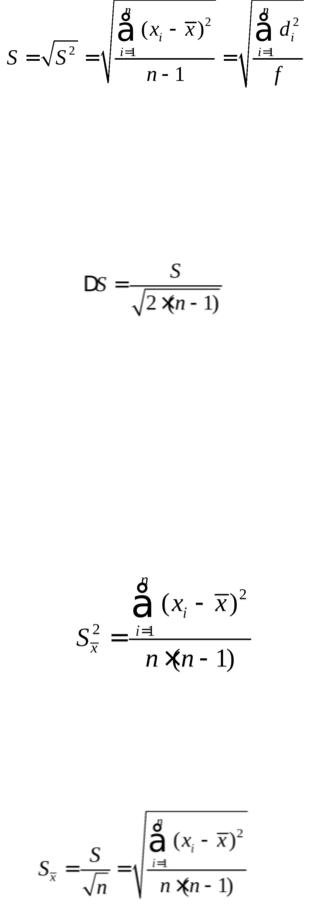
16
(6)
Эту величину называют также средним квадратич-
ным (квадратическим) отклонением или средней квадратичной погрешно-
стьюотдельного результата. Погрешность средней квадратичной погрешности может быть рассчитана по формуле:
(7)
Таким образом, при обработке результатов анализа обычно находят выборочное среднее х, а не генеральное, выборочную дисперсию S2 и выборочное стандартное отклонение S, а не σ2 и σ, характеризующие генеральную совокупность. Тем не менее, результаты случайной выборки позволяют оценить параметры генеральной совокупности.
Для оценки воспроизводимости вычисляют выборочную дисперсию среднего значения
(8)
и стандартное отклонение или среднюю квадратичную погрешность среднего результата :
(9)
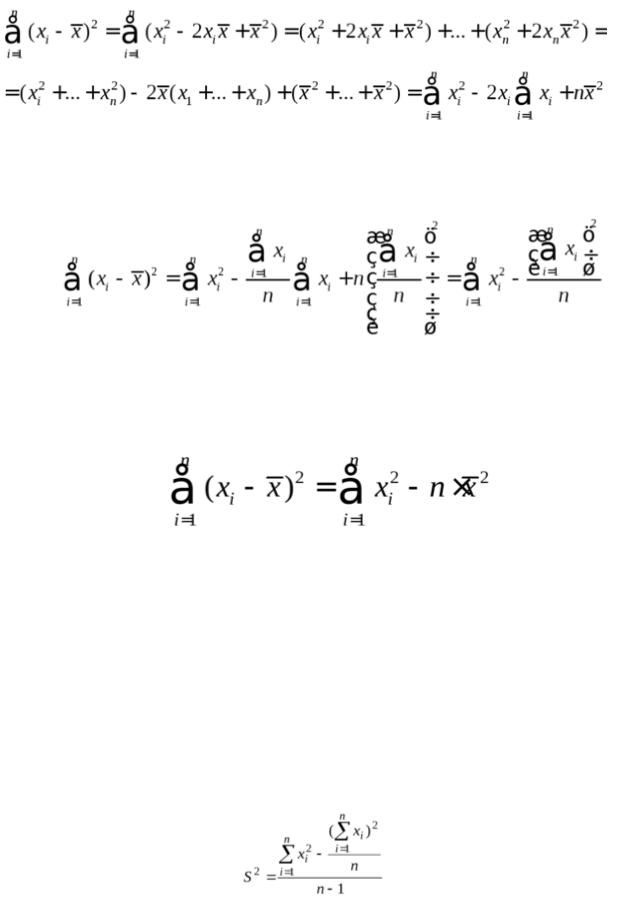
17
Сумму квадратов в формуле (3.4) можно преобразовать следующим образом:
(10)
Подставляя в (3.10) соотношение (3.2) получаем:
(11)
Или после упрощения:
(12)
Соотношение (11) проще и на первый взгляд кажется более удобным для практических вычислений. Однако при расчетах по этому соотношению получается малая разность двух больших величин, что неблагоприятно отражается на точности результата, особенно если используются значения Х, полученные при округлении обычным порядком, а не с запасом в несколько значащих цифр. В формуле (10)
округляемых значений нет, поэтому эффект малой разности двух больших величин сказывается в значительно меньшей степени. Таким образом, для практических вычислений оказывается целесообразным использовать соотношение (10). Тогда выражение для расчета дисперсии принимает вид:
(13)

18
и стандартное отклонение может быть рассчитано по формуле:
(14)
Пример: рассчитаем среднее значение, дисперсию и стандартное отклонение среднего результата при определении свинца Рb в сплаве (%) по следующим дан-
ным: 14,50; 14,43; 14,54; 14,45; 14,44; 14,52; 14,58; 14,40; 14,49.
По формуле (3.3), принимая А=14,50, получаем:
В соответствии с формулой (3.4) дисперсия будет равна:
По уравнению (3.12) величина S2 составляет:
Это полностью совпадает с результатом предыдущего расчета и не требуется находить разность , прежде чем взять соответствующий квадрат.
При использовании соотношения (11) значение S2 существенно зависит от округления среднего арифметического:

19
Приведенные результаты показывают, что истинное значение дисперсии в этом случае получается только при использовании среднего арифметического, имеющего не менее 6 цифр после запятой, поэтому расчеты с использованием соотношения (3.11) менее привлекательны, чем с использованием (3.10). Стандартное отклонение (квадратичную погрешность) рассчитываем по формуле (3.6):
и по (3.9) находим стандартное отклонение среднего результата:
В некоторых типах микрокалькуляторов, например в «Электроника МК-51», предусмотрен режим статистических расчетов, позволяющий получать величины и некоторые другие непосредственно после введения величин .
20
Лабораторная работа № 2.
Определение концентрационной зависимости в растворах электролитов методом прямой потенциометрии.
Потенциометрическое титрование относится к косвенным методам ана-
лиза и основано на установлении точки эквивалентности по резкому из-
менению потенциала индикаторного электрода.
Для нахождения конечной точки титрования используют зависимость равновесного потенциала индикаторного электрода от состава раствора. Из-
меряя потенциал электрода после добавления каждой порции раствора титран-
та, можно проследить за протеканием химической реакции в процессе титрова-
ния и по полученной кривой титрования найти конечную точку титрования.
На рис. 1 представлен вид кривых титрования, представленных в зави-
симости от необходимости в различной форме.
Интегральная кривая титрования является классической кривой, напри-
мер, при титровании кислоты основанием (рис.1а).
Для более точного нахождения точки эквивалентности часто строят дифференциальную кривую в координатах ∆E/∆V – V (рис.1б). На точку экви-
валентности указывает максимум полученной кривой, а отсчѐт по оси абсцисс,
соответствующий этому максимуму, даѐт объѐм титранта, израсходованного на титрование до точки эквивалентности.
Поскольку производная функции, имеющей максимум, в точке макси-
мума равна нулю, вторая производная потенциала по объѐму (∆2E/∆V2) в точке эквивалентности будет равна нулю. Это свойство также используется для нахо-
ждения точки эквивалентности (рис.1в).
В простом и удобном методе Грана точка эквивалентности определяется по графику в координатах ∆ V /∆ E – V. Перед точкой эквивалентности и после неѐ кривая Грана линейна, а сама точка эквивалентности находится как точка пересечения этих прямых (рис.1г). Достоинства и удобства метода
