4198

Для анализа процесса, протекающего в СМО, существенно знать основные параметры системы: число каналов n, интенсивность потока заявок λ, производительность каждого канала (среднее число заявок µ, обслуживаемое каналом в единицу времени), условия образования очереди (ограничения, если они есть).

В зависимости от этих параметров и выражаются характеристики эффективности работы СМО.

Одноканальная СМО с отказами

Пусть, система массового обслуживания состоит только из одного канала (n = 1) и на нее поступает пуассоновский поток заявок с интенсивностью λ, зависящей, в общем случае, от времени:

(2.1)

Заявка, заставшая канал занятым, получает отказ и покидает систему. В соответствии с классификацией Кендалла такая СМО обозначается

. Граф состояний системы показан на рис. 2.1.

Рисунок 2.3

Обслуживание заявки продолжается в течение случайного времени Tоб, распределенного по показательному закону с параметром µ:

(2.2)

Из этого следует, что «поток обслуживании» — простейший, с интенсивностью µ.

Требуется найти:

1)абсолютную пропускную способность СМО (A);

2)относительную пропускную способность СМО (q).

Рассмотрим единственный канал обслуживания как физическую систему S, которая может находиться в одном из двух состояний:

S0 — свободен, S1 — занят.

Из состояния S0 в S1 систему, очевидно, переводит поток заявок с интенсивностью λ; из S1 в S0 — «поток обслуживании» с интенсивностью µ.

Обозначим вероятности состояний p0(t) и p1(t). Очевидно, для любого момента t

(2.3)

Составим дифференциальные уравнения Колмогорова для вероятностей состояний согласно правилу, данному в § 3 гл. 4. Имеем:

(2.4)

Из двух уравнений (2.4) одно является лишним, так как p0 и p1 связаны соотношением (2.3). Учитывая это, отбросим второе уравнение, а в первое подставим вместо p1 его выражение (1 — p0):

11

Зная относительную пропускную способность q, легко найти абсолютную А. Они связаны соотношением:

(2.8)

В пределе, при t→∞, абсолютная пропускная способность тоже установится и будет равна

(2.9)

Зная относительную пропускную способность системы q (вероятность того, что пришедшая в момент t заявка будет обслужена), легко найти вероятность отказа:

(2.10)

Вероятность отказа Pотк есть не что иное, как средняя доля необслуженных заявок среди поданных. В пределе, при t→∞,

(2.11)

Упражнение 1. На основе формул (2.7-2.11) средствами пакета MS Excel построить графики зависимостей относительной и абсолютной пропускных способностей, а также вероятности отказа от параметров µ и , когда оба параметра изменяются в диапазоне от 0 до 1 с шагом 0.05. Для каждого изменяющегося параметра сформировать отдельные графики, приняв за константу, равную 0.5, µ и для соответствующих переменных и µ. Приблизительный результат показан на рис. 2.3.

Рисунок 2.5

Многоканальная СМО с отказами

Рассмотрим n-канальную СМО с отказами. Будем нумеровать состояния системы по числу занятых каналов (или, что в данном случае то же, по числу заявок, связанных с системой). Состояния будут:

S0 — все каналы свободны,

S1 — занят ровно один канал, остальные свободны, Sk — заняты ровно k каналов, остальные свободны, Sn — заняты все n каналов.

13

Граф состояний СМО представлен на рис. 2.4. Разметим граф, т. е. проставим у стрелок интенсивности соответствующих потоков событий. По стрелкам слева направо систему переводит один и тот же поток — поток заявок с интенсивностью λ. Если система находится в состоянии Sk (занято k каналов) и пришла новая заявка, система переходит (перескакивает) в состояние Sk+i.

Рисунок 2.6

Определим интенсивности потоков событий, переводящих систему по стрелкам справа налево.

Пусть система находится в состоянии S1 (занят один канал). Тогда, как только закончится обслуживание заявки, занимающей этот канал, система перейдет в S0; значит, поток событий, переводящий систему по стрелке S1> S0, имеет интенсивность µ. Очевидно, если обслуживанием занято два канала, а не один, поток обслуживании, переводящий систему по стрелке S2> S2 будет вдвое интенсивнее (2µ); если занято k каналов—в k раз интенсивнее (kµ). Проставим соответствующие интенсивности у стрелок, ведущих справа налево.

Пользуясь общими правилами, можно составить уравнения Колмогорова для вероятностей состояний:

(2.12)

Уравнения (2.12) называются уравнениями Эрланга. Естественными начальными условиями для их решения являются:

(в начальный момент система свободна).

Интегрирование системы уравнений (2.12) в аналитическом виде довольно сложно; на практике такие системы дифференциальных уравнений обычно решаются численно на ЭВМ. Такое решение дает нам все вероятности состояний

как функции времени.

Естественно, нас больше всего будут интересовать предельные вероятности состояний p0, p1, …, pk, …, pn, характеризующие установившийся режим работы СМО (при t→∞). Для нахождения предельных вероятностей

14

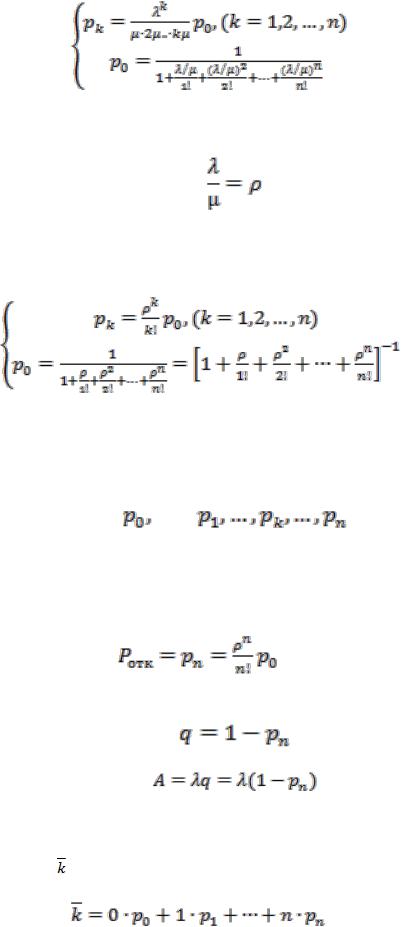
воспользуемся уже готовым решением задачи, полученным для схемы гибели и размножения. Согласно этому решению,

(2.13)

В этих формулах интенсивность потока заявок λ и интенсивность потока обслуживании (для одного канала) µ не фигурируют по отдельности, а входят только своим отношением λ/µ. Обозначим это отношение

и будем называть величину ρ «приведенной интенсивностью» потока заявок. Физический смысл ее таков: величина ρ представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.

С учетом этого обозначения, формулы (2.13) примут вид:

(2.14)

Формулы (2.14) называются формулами Эрланга. Они выражают предельные вероятности всех состояний системы в зависимости от параметров λ, µ и n (λ — интенсивность потока заявок, µ — интенсивность обслуживания, n — число каналов СМО).

Зная все вероятности состояний

можно найти характеристики эффективности СМО: относительную пропускную способность q, абсолютную пропускную способность A и вероятность отказа Pотк.

Действительно, заявка получает отказ, если приходит в момент, когда все n каналов заняты. Вероятность этого равна

(2.15)

Вероятность того, что заявка будет принята к обслуживанию (она же относительная пропускная способность q) дополняет Pотк до единицы:

Абсолютная пропускная способность:

Одной из важных характеристик СМО с отказами является среднее число занятых каналов (в данном случае оно совпадает со средним числом заявок, находящихся в системе). Обозначим это среднее число .

Величину можно вычислить непосредственно через вероятности p0, p1, …, pn по формуле:

(2.16)

15

как математическое ожидание дискретной случайной величины, принимающей значения 0, 1, ...., n с вероятностями р0, р1, ..., рn. Однако значительно проще выразить среднее число занятых каналов через абсолютную пропускную способность A, которую мы уже знаем. Действительно, A есть не что иное, как среднее число заявок, обслуживаемых в единицу времени; один занятый канал обслуживает в среднем за единицу времени µ заявок; среднее число занятых каналов получится делением A да

µ:

или, переходя к обозначению λ/µ= ρ,

(2.17)

Упражнение 2. На основе формул (2.15-2.17) средствами пакета MS Excel построить графики зависимостей вероятности отказа, абсолютной пропускной способности и среднего числа занятых каналов в зависимости от интенсивности входящих заявок и в зависимости от интенсивности потока обслуживания для СМО (шаг изменения интенсивностей - 10 в диапазоне от 10 до 150).

Одноканальная смо с ожиданием

Рассмотрим сначала простейшую из всех возможных СМО с ожиданием — одноканальную систему {n—1), на которую поступает поток заявок с интенсивностью λ; интенсивность обслуживания µ (т. е. в среднем непрерывно занятый канал будет выдавать µ обслуженных заявок в единицу (времени). Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания (рис.2.5).

Рисунок 2.5

Предположим, сначала, что количество мест в очереди ограничено числом m, т. е. если заявка пришла в момент, когда в очереди уже стоят m заявок, она покидает систему необслуженной. В дальнейшем, устремив m к бесконечности, мы получим характеристики одноканальной СМО без ограничений по длине очереди.

Будем нумеровать состояния СМО по числу заявок, находящихся в системе (как обслуживаемых, так и ожидающих обслуживания):

S0 — канал свободен,

S1 — канал занят, очереди нет,

S2 — канал занят, одна заявка стоит в очереди,

16

……………………………………………………

Sk — канал занят, k—1 заявок стоит в очереди,

……………………………………………………

Sm+i — канал занят, m заявок стоят в очереди.

Граф состояний СМО показан на рис. 2.5. Интенсивности потоков событий, переводящих в систему по стрелкам слева направо, все равны λ, а справа налево — µ. Действительно, по стрелкам слева направо систему переводит поток заявок (как только придет заявка, система переходит в следующее состояние), справа же налево — поток «освобождений» занятого канала, имеющий интенсивность µ, (как только будет обслужена очередная заявка, канал либо освободится, либо уменьшится число заявок в очереди).

Для представленного графа выражения предельных вероятностей состояний будет иметь вид:

(2.18)

где ρ=λ/µ.

Учитывая, что в знаменателе последней формулы (2.18) стоит геометрическая прогрессия с первым членом 1 и знаменателем ρ; суммируя эту прогрессию, находим:

(2.19)

Таким образом, формулы (2.18) окончательно примут вид:

(2.20)

Следует обратить внимание на то, что формула (2.19) справедлива только при ρ≠1 (при ρ=1 она дает неопределенность вида 0/0). Но сумму геометрической прогрессии со знаменателем ρ=1 найти еще проще чем по формуле (2.19): она равна m+2, и в этом случае р0= 1/(m+2).

Теперь требуется определить характеристики СМО: вероятность отказа Pотк, относительную пропускную способность q, абсолютную пропускную способность A, среднюю длину очереди , среднее число заявок, связанных с системой .

17

Очевидно, заявка получает отказ только в случае, когда канал занят и все m мест в очереди — тоже:

(2.21)

Находим относительную пропускную способность:

(2.22)

Абсолютная пропускная способность:

Найдем среднее число заявок, находящихся в очереди; определим эту величину как математическое ожидание дискретной случайной величины R

—числа заявок, находящихся в очереди:

Свероятностью p2 в очереди стоит одна заявка, с вероятностью р3 две заявки, вообще с вероятностью pk в очереди стоят k—1 заявок, наконец, с вероятностью pm+i в очереди стоят m заявок. Среднее число заявок в очереди получим, умножая число заявок в очереди на соответствующую вероятность и складывая результаты:

Вынесем в этом выражении ρ2р0 за скобки:

(2.23)

Выведем формулу для суммы, стоящей в скобках (этой формулой мы будем часто пользоваться в дальнейшем). Очевидно, рассматриваемая сумма представляет собой не что иное, как производную по ρ суммы

а для этого выражения можно воспользоваться формулой суммы геометрической прогрессии:

(2.24)

Продифференцировав (2.24) по ρ получим:

Итак, выражение для суммы, стоящей в скобках в правой части (2.23), найдено:

(2.25)

Подставляя его в (2.23), получим:

18

Учитывая выражение для p0 из (2.20), имеем:

или, окончательно,

(2.26)

Таким образом, мы вывели выражение для среднего числа заявок, ожидающих обслуживания в очереди. Выведем теперь формулу для среднего числа заявок, связанных с системой (как стоящих в очереди, так и находящихся под обслуживанием). Будем решать задачу следующим образом: рассмотрим общее число заявок K, связанных с системой, как сумму двух случайных величин: числа заявок, стоящих в очереди, и числа заявок, находящихся под обслуживанием:

где R — число заявок в очереди, Ω — число заявок под обслуживанием. По теореме сложения математических ожиданий

где — среднее число заявок в очереди, — среднее число заявок под обслуживанием.

Величину мы только что нашли; найдем величину . Так как канал - один, то случайная величина Ω может принимать только два значения: 0 или 1. Значение 0 она принимает, если канал свободен; вероятность этого равна

Значение 1 она принимает, если канал занят; вероятность этого равна

Отсюда находим математическое ожидание числа заявок, находящихся под обслуживанием:

Таким образом, среднее число заявок, связанных с СМО, будет

(2.27)

где величина определяется по формуле (2.26).

Выведем выражение еще для одной существенной характеристики СМО с ожиданием: среднего времени ожидания заявки в очереди. Обозначим его tож. Пусть заявка проходит в систему в какой-то момент времени. С вероятностью p0 канал обслуживания не будет занят, и ей не придется стоять

вочереди (время ожидания равно нулю). С вероятностью p1 она придет в систему во время обслуживания какой-то заявки, но перед ней не будет очереди, и заявка будет ждать начала своего обслуживания в течение времени 1/µ (среднее время обслуживания одной заявки). С вероятностью p2

вочереди перед рассматриваемой заявкой будет стоять еще одна, и время

19

ожидания в среднем будет равно 2/µ, и т. д. Вообще, с вероятностью pk пришедшая заявка застанет в системе k заявок и будет ждать в среднем k/µ единиц времени; здесь k может быть любым целым числом до m. Что же касается k=m+1, т. е. случая, когда вновь приходящая заявка застает канал обслуживания занятым и еще т заявок в очереди (вероятность этого pm+1), то время ожидания в этом случае также равно нулю, потому что заявка не становится в очередь (и не обслуживается) Поэтому среднее время ожидания будет:

Подставляя сюда выражения для p1,..., pm, получаем:

Преобразуем сумму в скобках, пользуясь формулой (2.25):

или, выражая p0 через ρ:

(2.28)

Сравнивая это выражение с формулой (2.26), замечаем, что

(2.30)

т. е. среднее время ожидания равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.

Выведем еще формулу для среднего времени пребывания заявки в системе. Обозначим Tсист случайную величину — время пребывания заявки в СМО. Эта случайная величина складывается из двух слагаемых (тоже случайных):

где Tож — время ожидания заявки в очереди, Θ — случайная величина, равная времени обслуживания Tоб, если заявка обслуживается, и нулю, если она не обслуживается (получает отказ). По теореме сложения математических ожиданий:

Упражнение 3. На основе формул (2.20-2.31) средствами пакета MS Excel построить графики зависимостей вероятности отказа, относительной и абсолютной пропускной способности СМО и среднего числа заявок в

20