3564

Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования

«Воронежский государственный лесотехнический университет им. Г.Ф. Морозова»

МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Методические указания к практическим занятиям

для студентов по направлению подготовки 23.04.01 – Технология транспортных процессов

Воронеж 2018

1

УДК 656.13

Денисов Г. А. Математические методы обработки экспериментальных данных [Электронная версия]: методические указания к практическим занятиям для студентов по направлению подготовки 23.04.01 – Технология транспортных процессов / Г.А. Денисов, В.А. Зеликов, Ю.В. Струков, Н.И. Злобина ; ВГЛТУ».– Воронеж, 2018. – 21 с. ЭБС ВГЛТУ.

Рецензент Заведующий кафедрой электротехники и автоматики агроинженерного факультета ФГБОУ ВПО «ВГАУ им. императора Петра I» д.т.н, проф. Афоничев Д.Н.

2

Введение

Обработка экспериментальных данных, полученных в результате измерений или наблюдений необходима для того, чтобы в дальнейшем с наибольшей эффективностью, корректно, использовать для построения эмпирических зависимостей статистические методы.

Первоначально проводят предварительную обработку, которая в основном состоит в отсеивании грубых погрешностей измерения или погрешностей, неизбежно имеющих место при переписывании цифрового материала или при вводе информации в считывающее устройство ЭВМ.

Грубые погрешности измерения (аномальные, или сильно выделяющиеся, значения) очень плохо поддаются определению, хотя интуитивно каждому экспериментатору ясно, что это такое.

Можно встретить указание, что аномальные значения измеряемой величины получаются в результате изменения условий эксперимента, однако это определение неполное.

Другим важным моментом предварительной обработки данных является проверка соответствия распределения результатов измерения закону нормального распределения. Если эта гипотеза неприемлема, то следует определить, какому закону распределения подчиняются опытные данные, и, если это возможно, преобразовать данное распределение к нормальному. Только после выполнения перечисленных выше операций можно перейти к построению эмпирических формул, применяя, например, метод наименьших квадратов.

Генеральная совокупность и выборка

Генеральной называют совокупность всех мыслимых значений наблюдений, которые могли бы быть сделаны при данном комплексе условий.

Генеральная совокупность может быть конечной и бесконечной. Данное выше определение генеральной совокупности можно считать строго обоснованным только для случаев конечных генеральных совокупностей.

Понятие бесконечной генеральной совокупности - математическая абстракция, как и представление о том, что измерить случайную величину можно бесконечное число раз. Приближенно бесконечную генеральную совокупность можно истолковать как предельный случай конечной генеральной совокупности. Результаты ограниченного ряда наблюдении х1, х2 ,..., хп случайной величины можно рассматривать как выборку из данной генеральной совокупности.

Относительные частоты можно истолковать как выборочные значения вероятностей случайных событий.

Если говорить о характеристиках распределений вероятностей, то характеристики теоретических распределений можно рассматривать как

3

характеристики, существующие в генеральной совокупности, а характеристики эмпирических распределений - как выборочные характеристики.

Характеристики распределения вероятностей в генеральной совокупности называют параметрами, а выборочные (эмпирические) значения характеристик

— оценками или статистиками.

Параметры обозначаются буквами греческого алфавита, а оценки — соответствующими буквами латинского алфавита.

Вычисление характеристик эмпирических распределений (выборочных характеристик). Моменты

Необходимо отметить, что речь идет только о непрерывно распределенных случайных величинах.

Пусть имеется ограниченный ряд наблюдений х1 , х2 , ..., хn случайной величины ξ. Среднее значение наблюдаемого признака можно определить по формуле:

среднее. Если вычислено среднее, то легко найти отклонение каждого наблюдения di от среднего:

называют дисперсией или вторым центральным моментом эмпирического распределения: S2=m2.

В случае одномерного эмпирического распределения произвольным моментом порядка k называется сумма k-х степеней отклонений результатов наблюдений от произвольного числа с, деленная на объем выборки п:

где k может принимать любые значения натурального ряда чисел. Если с = 0, то момент называют начальным. Начальным моментом первого порядка является выборочное среднее x . Действительно, x можно определить и по формуле:

4

которая равносильна формуле (1.1).

При с = x , как уже отмечалось при рассмотрении формулы (1.3), момент называется центральным. Первый центральный момент:

Второй центральный момент:

m2 1 n (xi x)2 n i 1

представляет собой дисперсию S2 эмпирического распределения.

Несмещенную оценку для σ2 (σ2 — дисперсия теоретического распределения), можно найти по формуле:

Выборочные среднеквадратические отклонения соответственно могут быть найдены по формулам:

Из других моментов чаще всего используют моменты третьего и четвертого порядка:

Выборочное значение коэффициента вариации υ, являющееся мерой относительной изменчивости наблюдаемой случайной величины, вычисляют по формуле:

x

5

Коэффициент вариации может быть вычислен и в процентах:

Выборочные значения характеристик распределения имеет смысл вычислять только в том случае, если выборка является случайной. Обычно на практике наблюдаемые значения х1 , х2 , ..., хn — величины случайные и отклонения их от среднего значения обусловлены погрешностями измерения, «ошибками природы» и т.д. В свою очередь, погрешности - результат действия многих факторов.

Если имеет место такой редкий случай, когда в распоряжении исследователя имеется вся генеральная совокупность и необходимо сделать из нее выборку, то используют один из методов рандомизации (случайного выбора). Удобнее всего при этом пользоваться таблицей случайных чисел.

Следует отметить, что к оценкам предъявляются требования

состоятельности, несмещенности и эффективности. Оценка параметра называется состоятельной, если по мере роста числа наблюдений п (т.е. при n N в случае конечной генеральной совокупности объема N и при n в случае бесконечной генеральной совокупности) она (оценка) стремится к оцениваемому теоретическому значению параметра. Например, для

дисперсии lim S 2 (n) 2 . Оценка параметра называется несмещенной, если при

n

любом числе наблюдений п ее математическое ожидание точно равно значению оцениваемого параметра. Удовлетворение требованию несмещенности устраняет систематическую погрешность, которая зависит от объема выборки п и в случае состоятельности стремится к нулю при n .

Следует четко разделять понятия состоятельности и несмещенности. Выше были определены две оценки для дисперсии: S2 и S 2 . Обе эти оценки состоятельны, но только вторая является несмещенной, так как первая содержит систематическую отрицательную погрешность — σ2/n (поскольку математическое ожидание MS2(n) = σ2 - σ2/n , которая с ростом п монотонно убывает. Из этого следует, что требование несмещенности особенно важно при малом количестве наблюдений.

Оценка параметра называется эффективной, если среди прочих оценок того же параметра она обладает наименьшей дисперсией.

Если имеется выборка х1 , х2 , ..., хn из нормальной генеральной совокупности, то среднее можно оценить двумя способами: по формуле (1.1) и с помощью выражения [xmin(n)+ xmax(n)]/2. Обе зти оценки обладают свойствами состоятельности и несмещенности, однако можно показать, что дисперсия при первом способе оценки равна σ2/п, а при втором π2σ2/(24ln n), т.е. существенно больше, так как первая оценка подвержена меньшим случайным колебаниям вокруг неизвестного истинного значения оцениваемого параметра.

6

Рассмотрим для практического использования наиболее простые методы отсева грубых погрешностей. Если в распоряжении экспериментатора имеется выборка небольшого объема п ≤ 25, то можно воспользоваться методом вычисления максимального относительного отклонения:

где xi - крайний (наибольший или наименьший) элемент выборки, по которой подсчитывались x и S - табличное значение статистики τ, вычисленной

при доверительной вероятности q 1 p .

Таким образом, для выделения аномального значения вычисляют:

Если это неравенство соблюдается, то наблюдение не отсеивают, если не соблюдается, то наблюдение исключают. После исключения того или иного наблюдения или нескольких наблюдений характеристики эмпирического распределения должны быть перечитаны по данным сокращенной выборки.

На практике обычно используют уровень значимости р=0,05 (результат получается с 95%-й доверительной вероятностью).

Полигон и гистограмма частот распределения

Если экспериментальные данные разделить на классы, то можно построить полигон и гистограмму частот.

Разбиение на классы можно выполнить по правилу Штюргеса. Число классов:

то такое распределение называют нормальным. Так как к коэффициентам а и b предъявляется требование: а, b > 0, то можно говорить о семействе кривых нормального распределения. С увеличением коэффициента а (Рис.1) кривая «вытягивается» в высоту; при увеличении коэффициента b кривая

«сплющивается».

8

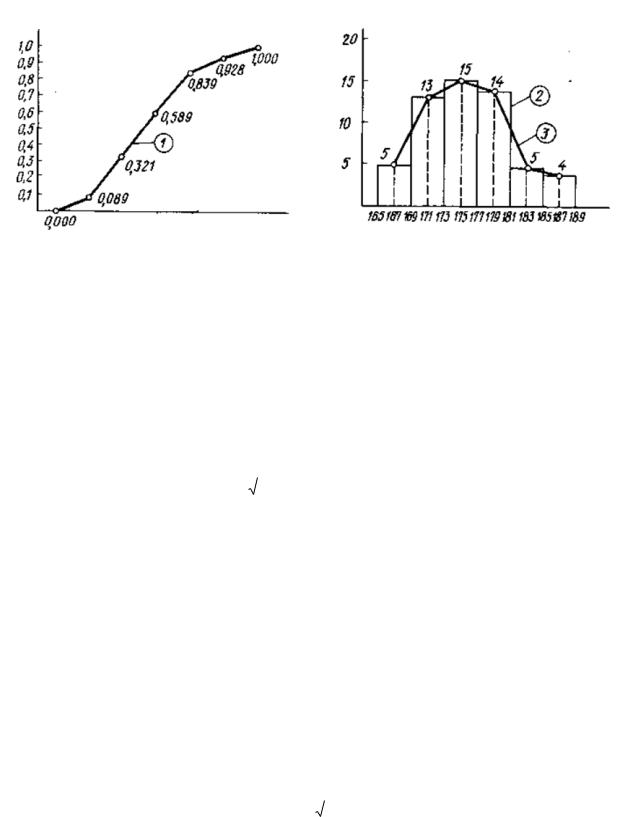
Рисунок 1 - Пример кумулятивной кривой гистограммы и полигона

Нормальное распределение обладает и другими важными свойствами, которые позволяют считать это распределение основой математической статистики. Рассмотрим эти свойства.

1°. Ордината у, которая определяет высоту кривой для каждой точки оси Ох (абсциссы), представляет собой плотность вероятности некоторого значения переменной х и определяется следующей формулой:

где σ - среднеквадратическое отклонение теоретического распределения; μ - среднее значение (математическое ожидание) теоретического

распределения.

Из формулы (1.21) следует, что нормальное распределение полностью определяется величинами μ и σ (π = 3,141593... и е = 2,718282... - математические постоянные). Математическое ожидание μ определяет положение кривой распределения относительно оси Ох. Среднеквадратическое отклонение σ определяет форму кривой. Чем больше σ (разброс данных), тем кривая становится более пологой (ее основание более широкое).

2°. Кривая нормального распределения симметрична относительно среднего значения.

3°. Максимум ординаты кривой:

что при σ = 1 составляет примерно 0,4. Если x , y 0 . Другими словами, очень большие и очень малые значения переменной х маловероятны.

4°. Примерно 2/3 всех наблюдений лежит в площади, отсекаемой перпендикулярами к оси Ох ( ). При большом объеме выборки примерно 90

9

% всех наблюдений лежит между — 1,64 σ и + 1,64 σ. Границы — 0,675 σ и + 0,675σ называют вероятными отклонениями; в этом интервале находится около 50 % всех наблюдений.

Для нормального распределения среднее, мода и медиана совпадают.

Для статистических методов построения эмпирических зависимостей очень важно, чтобы результаты наблюдений подчинялись нормальному закону распределения, поэтому проверка нормальности распределения - основное содержание предварительной обработки результатов наблюдений.

Проверка гипотезы нормальности распределения

Для не очень больших выборок (n < 120) можно найти простые рекомендации по проверке нормальности распределения. Для этого необходимо вычислить среднее абсолютное отклонение (САО) по формуле:

Для выборки, имеющей приближенно нормальный закон распределения, должно быть справедливо выражение:

Быструю проверку гипотезы нормальности распределения для сравнительно широкого класса выборок 3 < п < 1000 можно выполнить используя размах варьирования R. Подсчитывают отношение R / S и сопоставляют с критическими верхними и нижними границами этого отношения. Если R / S меньше нижней или больше верхней границы, то нормального распределения нет. Особенно важно, чтобы это условие соблюдалось при р = 0,10 (10%-ный уровень значимости).

Некоторое представление о близости эмпирического распределения к нормальному может дать анализ показателей асимметрии и эксцесса.