
1949
.pdf
11
Окончание табл. 3
№ |
а |
b |
u |
|
|
|
|
u |
|
|
|
u |
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
варианта |
|
|
|
AB |
|
|
|
BC |
|
|
CD |
|
|
AD |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
6 |
0,8 |
1 |
0,6y |
– 4,8 |
0,3125x2 – 4,2 |
0,56y – 4,56 |
0,3x |
– 4,8 |
||||||||||||
7 |
1 |
0,8 |
0,1y |
– 0,1 |
0,44x |
– 0,02 |
0,5y2 + 0,1 |
0,2x |
– 0,1 |
|||||||||||
8 |
0,8 |
1 |
0,2y |
+ 3,2 |
0,4375x2 +3,4 |
0,4y |
+ 3,28 |
0,1x |
+ |
3,2 |
||||||||||
9 |
1 |
0,8 |
0,3y |
+ 4 |
0,3x + 4,24 |
0,375y2 + 4,3 |
0,3x |
+ |
4 |
|||||||||||
10 |
0,8 |
1 |
0,2y2 |
+ 5 |
0,175x + 5,2 |
0,1y |
+ 5,24 |
0,375x2+5 |
||||||||||||
11 |
1,4 |
0,6 |
0,7y2 |
+ 3 |
1,62x |
+ 3,252 |
0,7y |
+ 5,1 |
1,5x |
+ |
3 |
|||||||||
12 |
0,6 |
1,4 |
0,25y + 9 |
1,25x2 + 9,35 |
0,25y + 9,45 |
0,75x + 9 |
||||||||||||||
13 |
1,4 |
0,6 |
0,2y |
+ 2 |
0,14x |
+ 2,12 |
0,2y |
+ 2,196 |
0,1x2 + 2 |
|||||||||||
14 |
0,6 |
1,4 |
0,6y2 |
+ 4 |
1,44x |
+ 5,176 |
1,2y |
+ 4,36 |
0,6x |
+ |
4 |
|||||||||
15 |
1,4 |
0,6 |
0,28y + 1 |
0,26x |
+ 1,168 |
0,7y2 + 1,28 |
0,2x |
+ |
1 |
|||||||||||
16 |
0,6 |
1,4 |
y + 8 |
|
0,6x + 9,4 |
y + 8,36 |
x2 + 8 |
|
||||||||||||
17 |
1,4 |
0,6 |
–3 |
|
|
0,17x |
– 3 |
0,07y– 2,804 |
0,1x2 – 3 |
|||||||||||
18 |
0,6 |
1,4 |
0,6y2 |
– 0,3 |
0,876 |
– 1,08x |
0,3y |
– 0,192 |
0,3x2– 0,3 |
|||||||||||
19 |
1,4 |
0,6 |
5 + 0,7y2 |
1,62x |
+ 5,252 |
0,7y |
+ 7,1 |
1,5x |
+ 5 |
|||||||||||
20 |
0,6 |
1,4 |
0,25y + 5 |
1,25x2 + 5,35 |
0,25y + 5,45 |
0,75x + 5 |
||||||||||||||
21 |
1 |
0,8 |
3 + 0,5y2 |
1,48x |
+ 3,32 |
y + 4 |
x + 3 |
|
||||||||||||
22 |
0,8 |
1 |
y |
|
|
1,5x + 1 |
1,6 + 0,6y2 |
2x |
|
|
||||||||||
23 |
1 |
0,8 |
2,1 + 0,3y |
0,1x + 2,34 |
0,375y2 + 2,2 |
0,1x |
+ 2,1 |
|||||||||||||
24 |
0,6 |
1,4 |
0,6y2 |
|
1,44x |
+ 1,176 |
1,2y |
+ 0,36 |
0,6x |
|
|
|||||||||
25 |
1,4 |
0,6 |
0,28y + 6 |
0,26x |
+ 6,168 |
0,7y2 + 6,28 |
0,2x |
+ 6 |
||||||||||||
Пример выполнения задания
Используя метод конечных разностей, составить приближенное решение задачи Дирихле для уравнения Лапласа
∂2u + ∂2u = 0 ∂x2 ∂y2
впрямоугольнике с вершинами A(0; 0), B(0; 0,8), C(1; 0,8), D(1; 0) с точностью
ε= 0,01 для шага h = 0,2. Граничные условия:
u AB = 0,5y2;
u BC = 0,4x2 + 0,32;
u CD = 0,4y + 0,4;
u AD = 0,2x.
Решение. Процесс решения разобьем на несколько этапов.
1. Построим прямоугольник ABCD, покроем его квадратной сеткой с
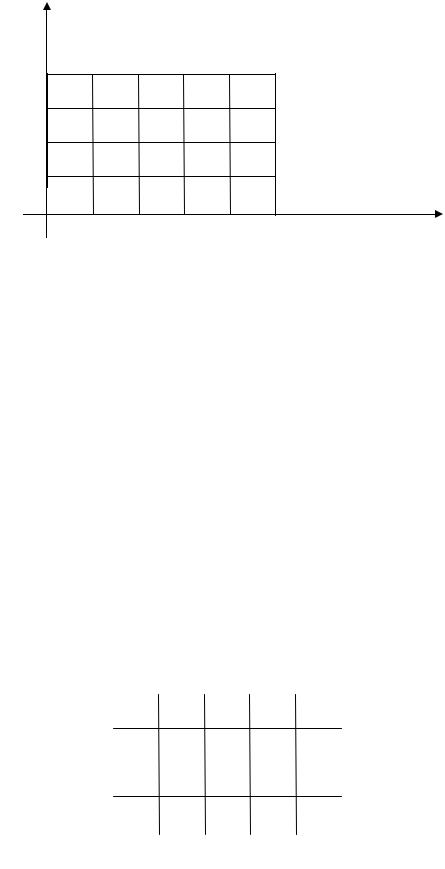
12
шагом h = 0,2 по осям Ox и Oy (рис.5). y
B |
C |
0,8
0,6
0,4
0,2
|
A |
|
|
|
|
|
|
D |
O |
|
|
|
|
|
|
x |
|
0,2 |
0,4 |
0,6 |
0,8 |
1 |
||||
Рис. 5
Вычислим значения искомой функции u(x; y) в граничных узлах сетки. Значения функции u(x; y) в узлах сетки на стороне AB найдем по формуле
u(x; y) = 0,5y2; имеем u0,0 = u(0; 0) = 0; u0,1 = u(0; 0,2) = 0,02;
u0,2 = u(0; 0,4) =0,08; u0,3 = u(0; 0,6) = 0,18; u0,4 = u(0; 0,8) =0,32.
На стороне ВС: u(x; y) = 0,4x2 + 0,32; u1,4 = u(0,2; 0,8) = 0,336;
u2,4 = u(0,4; 0,8) = 0,384; u3,4 = u(0,6; 0,8) = 0,464; u4,4 = u(0,8; 0,8) = 0,576; u5,4 = u(1; 0,8) = 0,72.
На стороне CD: u(x; y) = 0,4y + 0,4; u5,3 = u(1; 0,6) = 0,64;
u5,2 = u(1; 0,4) = 0,56; u5,1= u(1; 0,2) = 0,48; u5,0 = u(1; 0) = 0,4.
На стороне AD: u(x; y) = 0,4x; u1,0 = u(0,2; 0) = 0,08; u2,0 = u(0,4; 0) = 0,16; u3,0 = u(0,6; 0) = 0,24; u4,0 = u(0,8; 0) = 0,32.
Вычисленные значения функции u(x; y) в граничных узлах сетки сохраняются на любом шаге итерации. Отметим их на рисунке (рис. 6), соответствующем построенной выше (рис. 5) сетке. На этом же рисунке запишем обозначения ui,j искомых значений функции u(x; y) во внутренних узлах сетки.
0,32 |
0,336 |
0,384 |
0,464 |
0,576 |
|
0,72 |
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
0,18 |
|
u1,3 |
|
u2,3 |
u3,3 |
u4,3 |
|
0,64 |
|
0,08 |
|
u1,2 |
|
u2,2 |
u3,2 |
u4,2 |
|
|
0,56 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
0,02 |
|
u1,1 |
|
u2,1 |
u3,1 |
u4,1 |
|
0,48 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0,08 |
0,16 |
0,24 |
0,32 |
0,4 |
||||
Рис. 6
13
II. Для определения приближенных значений ui,j функции u(x; y) во внутренних узлах сетки запишем уравнение (10') для каждого такого узла, начиная с левого верхнего внутреннего узла, в следующем порядке:
u1,3 = 14 (0,18 + 0,336 + u2,3 + u1,2 ), u2,3 = 14 (u1,3 + 0,384 + u3,3 + u2,2 ), u3,3 = 14 (u2,3 + 0,464 + u4,3 + u3,2 ), u4,3 = 14 (u3,3 + 0,576 + 0,64 + u4,2 ), u1,2 = 14 (0,08 + u1,3 + u2,2 + u1,1),
u2,2 = 14 (u1,2 + u2,3 + u3,2 + u2,1), u3,2 = 14 (u2,2 + u3,3 + u4,2 + u3,1),
u4,2 = 14 (u3,2 + u4,3 + 0,56 + u4,1), u1,1 = 14 (0,02 + u1,2 + u2,1 + 0,08), u2,1 = 14 (u1,1 + u2,2 + u3,1 + 0,16), u3,1 = 14 (u2,1 + u3,2 + u4,1 + 0,24),
u4,1 = 14 (u3,1 + u4,2 + 0,48 + 0,32).
Получили систему уравнений для определения значений ui,j во внутренних узлах сетки. Решим эту систему итерационным методом Зейделя. Для каждого искомого значения ui,j запишем в указанном выше порядке соотношение (11):
= 14 (0,516 + u(2k,3−1) + u1(,k2−1) ),
= 14 (u1(,k3) + 0,384 + u3(k,3−1) + u(2k,2−1) ), = 14 (u(2k,3) + 0,464 + u(4k,3−1) + u3(k,2−1) ),
u(4k,3) = 14 (u3(k,3) +1,216 + u(4k,2−1) ),

14
u1(,k2) |
= |
1 |
(0,08 + u1(,k3) + u(2k,2−1) + u1(,k1−1) ), |
|
||
|
|
4 |
|
|
|
|
u(2k,2) = |
1 |
(u1(,k2) + u(2k,3) + u3(k,2−1) + u(2k,1−1) ), |
|
|||
|
|
4 |
|
|
|
|
u3(k,2) = |
1 |
(u(2k,2) + u3(k,3) + u(4k,2−1) + u3(k,1−1) ), |
(12) |
|||
|
|
4 |
|
|
|
|
u(4k,2) |
= |
1 |
(u3(k,2) + u(4k,3) + 0,56 + u(4k,1−1) ), |
|
||
|
|
4 |
|
|
|
|
u1(,k1) |
= |
1 |
(0,1 + u1(,k2) + u(2k,1−1) ), |
|
||
|
|
4 |
|
|
|
|
u(2k,1) |
= |
1 |
(u1(,k1) + u(2k,2) |
+ u3(k,1−1) + 0,16), |
|
|
|
|
4 |
|
|
|
|
u3(k,1) |
= |
1 |
(u(2k,1) + u3(k,2) |
+ u(4k,1−1) + 0,24), |
|
|
|
|
4 |
|
|
|
|
u(k) |
= |
1 |
(u(k) |
+ u(k) |
+ 0,8). |
|
4,1 |
|
4 |
3,1 |
4,2 |
|
|
Для вычислений по этим формулам нужно определить начальные значения
ui(,0j) для внутренних узлов сетки, которые могут быть найдены каким-либо способом.
III. Для того, чтобы получить начальные значения ui(,0j) (начальное приближенное решение задачи), будем считать, что для каждого фиксированного j (j = 1, 2, 3) разность K j = ui(+0)1, j − ui(,0j) одинакова при всех
i = 0, 1, 2, 3, 4, то есть разница Kj между значениями ui(,0j) в любых двух
соседних узлах любой горизонтали на прямоугольнике (рис. 5), не являющейся верхней или нижней горизонталью, одинакова.
Пусть j = 1. Рассмотрим горизонталь рисунка 5 с граничными точками
(0; 0,2) и (1; 0,2) (рис. 7).
0,02 |
u1,1(0) |
u(0)2,1 |
u3,1(0) |
u(0)4,1 |
0,48 |
|
|
|
|
||
(0; 0,2) |
|
|
|
|
(1; 0,2) |
|
|
|
Рис. 7 |
|
|
Над горизонталью рисунка 7 записаны значения ui(,01) (i =0,1, 2, 3, 4, 5) |
в узлах |
||||||
этой горизонтали. Так как отрезок [0,02; 0,48] точками |
(0) |
, |
(0) |
|
(0) |
, |
(0) |
u1,1 |
u2,1 |
, u3,1 |
u4,1 |
||||

15
разбит на 5 равных частей, то K1 = (0,48 – 0,02) / 5 = 0,092. Отсюда получаем u1(,01) =0,02 + K1 = 0,02 + 0,092 =0,112; u(20,1) = u1(,01) + K1 =0,112 + 0,092 = 0,204;
u3(0,1) = u(20,1) + K1 = 0,204 + 0,092 = 0,296; u(40,1) = u3(0,1) + K1 =0,296 + 0,092 =0,388.
Аналогично найдем значения ui(,0j) во внутренних узлах других горизонталей (j = 2, 3). Для горизонтали с граничными точками (0; 0,4) и (1; 0,4) (рис. 8)
0,08 |
u1,2(0) u(0)2,2 |
u3,2(0) |
u(0)4,2 |
0,56 |
|
|
|
|
|
||
(0; 0,4) |
|
|
|
|
(1; 0,4) |
|
|
|
Рис. 8 |
|
|
К2 = (0,56 – 0,08) / 5 = 0,096 |
и, следовательно, u1(,02) = 0,08 + 0,096 = 0,176; |
||||
u(20,2) = 0,176 + 0,096 = 0,272; |
u3(0,2) = 0,272 + 0,096 = 0,368; u(40,2) = 0,368 + |
||||
+ 0,096 = 0,464.
Для горизонтали с граничными точками (0; 0,6) и (1; 0,6) (рис. 9)
0,18 |
u1,3(0) |
u(0)2,3 |
u3,3(0) |
u(0)4,3 |
0,64 |
|
|
|
|
||
(0; 0,6) |
|
|
|
|
(1; 0,6) |
|
|
|
Рис. 9 |
|
|
K3= (0,64 – 0,18) / 5 = 0,092 и, следовательно, u1(,03) = 0,18 + 0,092 = 0,272;
u(20,3) = 0,272 + 0,092 = 0,364; u3(0,3) = 0,364 + 0,092 = 0,456; u(40,3) = 0,456 + + 0,092 = 0,548.
Все полученные значения представим в табл. 4.
Таблица 4
0,8 |
|
0,32 |
0,336 |
0,384 |
0,464 |
0,576 |
0,72 |
0,6 |
|
0,18 |
0,272 |
0,364 |
0,456 |
0,548 |
0,64 |
0,4 |
|
0,08 |
0,176 |
0,272 |
0,368 |
0,464 |
0,56 |
0,2 |
|
0,02 |
0,112 |
0,204 |
0,296 |
0,388 |
0,48 |
0 |
|
0 |
0,08 |
0,16 |
0,24 |
0,32 |
0,4 |
yj |
xi |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
|
|||||||
|
|
|
|
|
|
|
16
IV. Вычисление элементов ui(1, j) первой итерации производим по формулам (12) в том порядке, в котором записаны эти формулы:
u1(1,3) = 14 (0,516 + u(20,3) + u1(,02) ) = 14 (0,516 + 0,364 + 0,176) =0,264;
u(1) |
= 1 |
(u(1) + 0,384 + u(0) |
+ u(0) ) = 1 (0,264 + 0,384 + 0,456 + 0,272) = 0,344 |
||||||||||||||
2,3 |
4 |
1,3 |
3,3 |
2,2 |
4 |
|
|
|
|
|
|
|
|||||
и так далее. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Полученные значения ui(1, j) первой итерации представим в табл. 5. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5 |
|
|
|
0,8 |
|
0,32 |
|
0,336 |
|
0,384 |
|
|
0,464 |
0,576 |
0,72 |
|
||
|
|
|
0,6 |
|
0,18 |
|
0,264 |
|
0,344 |
|
|
|
0,431 |
0,528 |
0,64 |
|
|
|
|
|
0,4 |
|
0,08 |
|
0,182 |
|
0,275 |
|
|
0,367 |
0,461 |
0,56 |
|
||
|
|
|
0,2 |
|
0,02 |
|
0,122 |
|
0,213 |
|
|
0,302 |
0,391 |
0,48 |
|
||
|
|
|
0 |
|
0 |
|
0,08 |
|
|
0,16 |
|
|
|
0,24 |
0,32 |
0,4 |
|
|
|
|
yj |
|
0 |
|
0,2 |
|
|
0,4 |
|
|
0,6 |
0,8 |
1 |
|
|
|
|
|
xi |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Максимальное |
различие |
max |
|
ui(1, j) − ui(,0j) |
|
|
|
по всем i, j |
элементов нулевой и |
||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
i, j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
первой итераций (погрешность первой итерации) равно 0,025. Так как 0,025 > > ε = 0,01, то для достижения заданной точности вычислений уточнение решения нужно продолжить.
Значения ui(,2j) второй итерации представлены в табл. 6.
Таблица 6
0,8 |
|
0,32 |
0,336 |
0,384 |
0,464 |
0,576 |
0,72 |
|
0,6 |
|
0,18 |
0,261 |
0,338 |
|
0,424 |
0,525 |
0,64 |
0,4 |
|
0,08 |
0,185 |
0,276 |
0,366 |
0,461 |
0,56 |
|
0,2 |
|
0,02 |
0,125 |
0,216 |
0,303 |
0,391 |
0,48 |
|
0 |
|
0 |
0,08 |
0,16 |
|
0,24 |
0,32 |
0,4 |
yj |
xi |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
Погрешность второй итерации равна 0,007. Так как 0,007 < ε = 0,01, то построение последовательности итераций завершаем. Последние значения округляем до сотых долей и получаем ответ в виде табл. 7.

17
Таблица 7
0,8 |
|
0,32 |
0,34 |
0,38 |
0,46 |
0,58 |
0,72 |
|
0,6 |
|
0,18 |
0,26 |
0,34 |
0,42 |
0,53 |
0,64 |
|
0,4 |
|
0,08 |
0,19 |
0,28 |
0,37 |
0,46 |
0,56 |
|
0,2 |
|
0,02 |
0,13 |
0,22 |
0,30 |
0,39 |
0,48 |
|
0 |
|
0 |
0,08 |
0,16 |
|
0,24 |
0,32 |
0,4 |
yj |
xi |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ СТРУНЫ МЕТОДОМ ДАЛАМБЕРА
Задача Коши для уравнения колебаний струны
∂2u |
= a |
2 |
∂2u |
(a |
2 |
= const > 0) |
(13) |
∂t2 |
|
∂x2 |
|
||||
|
|
|
|
|
|
ставится следующим образом.
Требуется найти функцию u(x; t), удовлетворяющую уравнению (13) при x (−∞, + ∞), t (0, + ∞) и начальным условиям
u(x; 0) = φ(x), |
∂u(x; 0) |
= ψ(x) (– ∞ < x < + ∞), |
(14) |
|
∂t |
|
|
где φ(x), ψ(x) – заданные функции.
Пусть α(ξ) −произвольная дважды дифференцируемая на промежутке
(– ∞, + ∞) функция. Тогда функция u1(x; t) = α(x – at) (a > 0) является решением уравнения (13). Действительно,
∂u1 |
′ |
∂2u1 |
|
′′ |
|
∂x |
|
|
|||
=α (x −at), |
∂x2 |
=α (x − at), |
|||
∂u1 |
′ |
∂2u1 |
= a |
2 |
′′ |
∂t |
= −a α (x −at), |
∂t2 |
|
α (x −at), |
|
поэтому |
∂2u1 |
=a2 |
∂2u1 |
при x (−∞, + ∞), |
t (0, + ∞) . |
|
∂t2 |
|
∂x2 |
|
|
Аналогично |
устанавливается, что если |
β(η) − произвольная дважды |
|||
дифференцируемая на промежутке (−∞, + ∞) функция, то функция
u2(x; t) = β(x + at) является решением уравнения (13). Если сложить эти два решения, то снова получим решение уравнения (13)
u(x; t) = α(x – at) + β(x + at). (15)
Можно доказать, что в таком виде записывается любое решение уравнения (13). Будем предполагать, что функция φ(x) дважды дифференцируема и функция
ψ(x) один раз дифференцируема на промежутке (– ∞, + ∞).
18
Определим функции α и β таким образом, чтобы выполнялись начальные условия (14):
u(x; 0) = α(x) + β(x) = φ(x),
∂u(x; 0) = −aα′(x) + aβ′(x) = ψ(x).
∂t
Разделим обе части последнего равенства на а и проинтегрируем от 0 до х. Получим
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|||
∫(−α′(τ) +β′(τ))dτ = −α(x) +β(x) + α(0) −β(0) = |
∫ψ(τ)dτ. |
||||||||||||||||||
a |
|||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда −α(x) +β(x) = |
|
1 |
x ψ(τ)dτ + c0 , где с0 = β(0) – α(0). |
||||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
a ∫ |
|
|
|
|
|
|
|
|
|
|
||||
Имеем два равенства |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||
|
α(x) +β(x) =ϕ(x), −α(x)+β(x) = |
1 |
ψ(τ)dτ + c0 . |
||||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a ∫ |
|
|
|
|
|
|
|
||
Складывая их и вычитая, получаем |
0 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
α(x) = 1 |
|
1 |
x |
|
|
|
c0 |
|
β(x) = 1 ϕ(x) |
|
1 |
|
x |
|
c0 |
|
|||
ϕ(x) − |
∫ |
ψ(τ)dτ − |
, |
+ |
|
∫ |
ψ(τ)dτ + |
. |
|||||||||||
2a |
|
2a |
|
||||||||||||||||
2 |
|
0 |
2 |
|
2 |
|
|
|
0 |
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, мы определили функции α(x) и β(х). Поэтому решение по формуле (15) принимает вид
|
ϕ(x − at) + ϕ(x + at) |
|
1 |
x +at |
1 |
x −at |
|
u(x; t) = |
+ |
∫ψ(τ)dτ − |
∫ψ(τ)dτ. |
||||
2 |
2a |
2a |
|||||
|
|
0 |
0 |
||||
|
|
|
|
|
Заметим, что неизвестная величина с0 не вошла в последнюю формулу. Меняя местами пределы интегрирования в последнем интеграле, получаем окончательную формулу – формулу Даламбера
|
ϕ(x − at) + ϕ(x + at) |
|
1 |
x +at |
|
u(x; t) = |
+ |
∫ψ(τ)dτ. |
|||
2 |
2a |
||||
|
|
x −at |
|||
|
|
|
|
Она была получена французским математиком Даламбером в 1750 году.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
Используя формулу Даламбера, найти функцию u(x; t), удовлетворяющую уравнению
∂2u |
= a |
2 |
∂2u |
(– ∞ < x < + ∞, 0 < t < + ∞) |
∂t2 |
|
∂x2 |
||
|
|
|
и начальным условиям
|
|
|
19 |
|
|
|
|
|
|
|
|
u(x; 0) = f(x), |
∂u(x; 0) |
=g(x) |
|
(– ∞ < x < + ∞). |
|||||
|
|
|
∂t |
|
|
|
|
|
|
|
Значение a |
и функции f(x), g(x) заданы в табл. 8. |
|
|
Таблица 8 |
||||||
|
|
|
|
|
|
|
|
|
|
|
№ варианта |
|
a |
|
|
|
|
f(x) |
g(x) |
||
1 |
|
2 |
|
|
|
ex + 1 |
xcos x |
|||
2 |
|
1 |
|
|
|
cos x |
x ·e–x |
|||
3 |
|
2 |
|
|
|
x2 |
xsin2x |
|||
4 |
|
1 |
|
|
|
x3 |
x2sin x |
|||
5 |
|
2 |
|
|
|
3x |
1 x cos3x |
|||
|
|
|
|
|
|
|
|
|
|
2 |
6 |
|
1 |
|
|
|
|
|
1 |
|
xe–3x |
|
|
|
|
|
|
|
x2 +1 |
|
|
|
7 |
|
2 |
|
|
|
e–x |
x·5x |
|||
8 |
|
1 |
|
|
|
ex 2 |
sinx ·cos 2x |
|||
9 |
|
2 |
|
|
|
x3 |
cos x ·cos 3x |
|||
10 |
|
1 |
|
|
|
e1 – x |
sin x ·sin5x |
|||
11 |
|
2 |
|
|
|
x2 + 1 |
excos x |
|||
12 |
|
1 |
|
|
|
x + ex |
exsin x |
|||
13 |
|
2 |
|
|
|
x2 + 2x |
x2e–x |
|||
14 |
|
1 |
|
|
|
e |
−x3 |
x2cos2x |
||
|
|
|
|
|
|
|
|
|
||
15 |
|
2 |
|
|
|
sinx |
x·cos2x |
|||
16 |
|
1 |
|
|
|
(x + 1)2 |
xex |
|||
17 |
|
2 |
|
|
|
x3 + 1 |
x ·2–x |
|||
18 |
|
1 |
|
|
|
x + ex |
x ·e–2x |
|||
19 |
|
2 |
|
|
|
e |
−x 2 |
x sin3x |
||
|
|
|
|
|
|
|
|
|
||
20 |
|
1 |
|
|
|
sin (x2) |
sin2x · sin4x |
|||
21 |
|
2 |
|
|
|
cos(x+5) |
cosx · cos5x |
|||
22 |
|
1 |
|
|
|
esin x |
cos3x·sin5x |
|||
23 |
|
2 |
|
|
|
|
ex 2 −1 |
x · 2x |
||
24 |
|
1 |
|
|
|
ln(x2 + 1) |
e–x · x2 |
|||
25 |
|
2 |
|
|
|
sin (x3) |
cos3x ·cos 4x |
|||
Пример выполнения задания
Используя формулу Даламбера, найти функцию u(x; t), удовлетворяющую уравнению
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2u |
= |
∂2u |
|
(– ∞ < x < + ∞, 0 < t < + ∞) |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
∂t2 |
∂x2 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и начальным условиям |
|
|
∂u(x; 0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
u(x; 0) = |
|
|
x |
|
|
, |
|
=sin x |
(– ∞ < x < + ∞). |
|
|
|
|
|
|
|
|||||||||||
|
|
|
+ x2 |
|
|
∂t |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение. Пользуясь формулой Даламбера, получаем |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
1 |
|
x − t |
|
|
|
|
|
|
|
x + t |
|
|
|
1 x +t |
|
1 |
|
x − t |
|
|
|
x + t |
|
|
|
|||
u(x; t) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫sin τdτ = |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
+ (x − t) |
2 |
|
+ |
|
|
+ (x + t) |
2 |
+ |
2 |
|
+ (x − t) |
2 + |
1 + (x + t) |
2 |
|
+ |
|||||||||||
|
1 |
|
|
1 |
|
|
2 x −t |
|
1 |
|
|
|
|
|
|||||||||||||||
+sin x sin t.
МЕТОД ПРОДОЛЖЕНИЙ РЕШЕНИЯ СМЕШАННОЙ ЗАДАЧИ, ОПИСЫВАЮЩЕЙ КОЛЕБАНИЯ ПОЛУБЕСКОНЕЧНОЙ СТРУНЫ С ЗАКРЕПЛЕННЫМ ЛЕВЫМ КОНЦОМ
Смешанная задача, описывающая колебания полубесконечной струны с закрепленным левым концом, для уравнения (13) ставится следующим образом.
Требуется найти функцию u(x; t), удовлетворяющую уравнению (13) при x (0, + ∞), t (0, + ∞), начальным условиям
u(x; 0) = ϕ(x), |
∂u(x; 0) |
= ψ(x) (0 ≤ x < +∞), |
|
∂t |
|
и граничному условию
u(0; t) = 0 (0 ≤ t < + ∞),
где ϕ(x), ψ(x) − заданные функции.
(16)
(17)
Будем предполагать, что функция φ(x) дважды дифференцируема на промежутке [0, +∞ ), функция ψ(x) один раз дифференцируема на промежутке
[0, +∞) и ϕ(0) =ϕ′′(0) = ψ(0) = 0.
Введем функции Φ(x) и Ψ(x) , которые будут являться нечетными
продолжениями функций ϕ(x) и ψ(x), входящих в условия (16): |
|
||||||||
ϕ(x) |
при |
x ≥0, |
|
|
|
|
|||
Φ(x) = |
|
при |
x <0, |
|
|
||||
− ϕ(−x) |
|
|
|||||||
ψ(x) |
при |
x ≥0, |
|
|
|||||
Ψ(x) = |
|
при |
x |
< 0. |
|
|
|||
− ψ(−x) |
|
|
|||||||
Согласно методу Даламбера функция |
|
|
|
|
x +at |
|
|||
u(x; t) = Φ(x −at) + Φ(x + at) |
|
1 |
|
||||||
+ |
∫Ψ(τ)dτ |
(18) |
|||||||
2a |
|||||||||
|
2 |
|
|
|
|
x −at |
|
||
|
|
|
|
|
|
|
|
||
