Здоровцева Г.Г. Контролируемая самостоятельная работа студентов по курсу «Общая физика». Тема «Механика точки»

Нормальное ускорение an запишем по определению и выразим его через путь s по заданному в условии задачи модулю скорости:

После подстановки (3) и (4) в (2), получим

tgφ = 2s .

R

Задача решена.

Задача 1.5. Уравнения движения точки имеют вид x = Asin ωt, y = Bcosωt , где A, В и ω – постоянные. Найти уравнение траектории, скорость, ускорение, а также модули скорости и ускорения. Указать направление движения точки по траектории.

Решение. Движение задано координатным способом. Характерная особенность этой задачи в том, что время в кинематических уравнениях движения входит под знак синуса и косинуса.

Чтобы найти уравнение траектории надо из уравнений движения исключить время. Сделаем это следующим образом.

Перепишем уравнения движения:

11

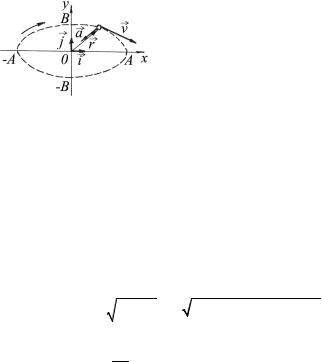
Траектория точки – эллипс с полуосями А и В.

Чтобы определить направление движения точки по траектории вернёмся к уравнениям движения. Из них следует, что в начальный момент (t = 0) точка имела координаты х(0) = 0, y(0) = В. При возрастании времени движения координата x = Asin ωt точки растёт, а координата y = Bcosωt – убывает. Из чего следует, что точка движется по траектории в направлении, указанном на рис. 1.4

стрелкой – «по часовой стрелке».

Рис. 1.4

Проекции скорости на оси координат

находим, дифференцируя по времени соответствующие координаты

направлена в положительном направлении оси х, что подтверждает сделанное ранее заключение о направлении движения.

Запишем вектор скорости точки через его составляющие:

dt

Полученное выражение можно записать короче, если ввести в

В любой точке траектории ускорение направлено к началу координат.

Возвращаясь к исходному выражению a , найдем модуль ускорения по его проекциям:

12

Задача решена.

Задача 1.6. Точка движется по дуге окружности радиуса R по закону l = Asin ωt , где l – расстояние, отсчитываемое от начального положения точки вдоль дуги, А и ω – постоянные. Найти скорость и ускорение в точках l = 0 и l = ± A.

Решение. Движение задано естественным способом. Особенность задачи в том, что надо найти скорость и ускорение не как функции времени, а в определённых точках траектории.

Находим проекцию скорости по определению:

Учитывая, что скорость направлена по касательной к траектории, записываем

Ускорение представляем суммой тангенциальной и нормальной составляющих:

Выражения (2) и (3) дают возможность вычислить скорость и ускорение в любой момент времени. Чтобы ответить на вопросы задачи, надо найти те моменты времени, в которые точка будет проходить начальное положение (l = 0) и моменты максимального удаление от него (l = ± A).

Найдём эти моменты времени.

В точке l = 0 движущаяся точка будет находиться всякий раз, когда sin ωt = 0 , т.е. при условии ωt = nπ , где n = 0, 1, 2, …

В точках l = ± A движущаяся точка будет находиться, когда

sin ωt = ±1 , т.е. при условии ωt = (2n +1) π , где n = 0, 1, 2, … 2

13

Получим скорость в заданных точках траектории, подставляя в

(2) соответствующие значения ωt .

В точке l = 0, v = ± Aωτ. Знак «+» соответствует условию, при котором ωt = 0, 2π, 4π, .... Знак «–» соответствует условию, при котором ωt = π, 3π, 5π, ... В точках l = ± A, v = 0 .

Найдем ускорения в этих характерных точках траектории, ис-

Резюме. Осмыслим результаты. Материальная точка выходит из начального положения l(0) = 0 и движется по дуге окружности между точками +A и –A.

В стадиях движения от начального положения к точкам ± A скорость v и тангенциальное ускорение aτ имеют противополож-

ные направления. Вследствие чего материальная точка тормозится и останавливается. Скорость в точках ± A обращается в ноль – они являются для нее «точками поворота». В ноль в этих точках обращается и нормальное ускорение.

После остановки материальная точка поворачивает назад. В стадиях движения от «точек поворота» к начальному положению скорость v и тангенциальное ускорение aτ сонаправлены –

скорость материальной точки увеличивается. Максимального значения скорость достигает при прохождении материальной точкой положения l = 0. В этой точке нормальное ускорение принимает максимальное значение, а тангенциальное обращается в ноль.

Задача 1.7. Движение точки задано уравнениями x = (v0 cosα0 )t,

скорости точки и горизонтом, g – ускорение свободного падения. Найти:

1)перемещение точки в функции времени,

2)средний вектор скорости v за первые t секунд движения;

14

3)траекторию точки;

4)координаты наивысшего положения точки;

5)проекции скорости на координатные оси в тот момент, когда точка находится на оси OX;

6)нормальное и тангенциальное ускорения точки для любого момента времени;

7)радиус кривизны траектории в начальный момент времени и

ввершине траектории.

Решение. Заданные уравнения представляют собой кинематические уравнения движения тела, брошенного с поверхности Земли с начальной скоростью v0 , составляющий угол α с горизонтом.

Эту задачу можно рассматривать как итоговую ко всей кинематике. Движение здесь задано координатным способом. Но поставленные вопросы требуют умения работать с величинами и понятиями, характерными не только для координатного способа, но и для векторного и естественного.

1. Перемещение по определению – приращение радиус-вектора. Из заданных уравнений движения следует, что точка движется из начала координат (при t = 0, x = 0, y = 0), поэтому

Эту запись можно упростить, если принять во внимание, что

Тогда перемещение примет вид

2. Средний вектор скорости по определению

v = ∆r .

∆t

Для первых t секунд (∆t = t) рассматриваемого движения

3. Уравнение траектории находим, исключая время из уравне-

x

ний движения. Из первого уравнения t = v0 cosα , подставляя это

15

выражение во второе уравнение движения, после несложных преобразований получим

Траектория точки представляет собой ветвь параболы.

4. Чтобы найти координаты наивысшего положения точки воспользуемся тем соображением, что в высшей точке траектории касательная к траектории должна лежать горизонтально, иначе говоря, используем математическое условие максимума функции y(x):

Координату xмакс, при которой точка будет находиться на вершине своей траектории, находим из последнего уравнения

Координату yмакс наивысшего положения точки на траектории («максимальную высоту подъема») находим, подставляя (4) в уравнение траектории (3):

5. Чтобы ответить на следующий вопрос задачи, получим сначала проекции скорости на оси x и y для любого момента времени:

Как видно, горизонтальная проекция скорости остается постоянной в течение всего времени движения.

Что бы найти vy в момент, когда точка окажется на оси OX, найдем этот момент из условия, что y = 0:

Как следует из уравнения (7), точка будет иметь координату y = 0 дважды: при t1 = 0 – это начало движения и в момент

Подставляя t1 и t2 в (6) получаем соответственно

16

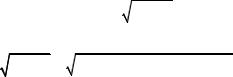
vy (t1) = v0 sinα , vy (t2 ) = −v0 sinα .

На данном этапе решения задачи, когда мы получили выражения для проекций скорости, можно вернуться к нахождению максимальной высоты подъема точки, не прибегая к математическому методу нахождения максимума функции. Действительно, когда тело поднимается до высшей точки траектории, перед тем, как оно начнет опускаться, вертикальная проекция его скорости обратится в ноль:

vy = v0 sinα − gt = 0.

Отсюда мы найдем время подъема или, иначе, момент прохождения телом вершины траектории:

Подставляя (9) в уравнение движения вдоль оси y, получим максимальную высоту подъема (координату умакс наивысшего положения точки):

6. Обратимся к нахождению нормального и тангенциального ускорений. Вспомним соответствующие формулы:

Найдем модуль скорости

Дифференцируя (10) по времени, получаем

Нормальное ускорение непосредственно по формуле для an найти нельзя, так как неизвестен радиус кривизны R. В каждой точке траектории он будет свой, поэтому выразим an через a и aτ:

17

Заметим, что результат (13) ясен и без указанных вычислений, так как тело свободно движется в поле тяжести и никакого другого ускорения, кроме ускорения свободного падения g , иметь не может.

Найдем нормальное ускорение, подставляя в (12) выражения (11) и (13) и произведя необходимые алгебраические операции:

7. Радиус кривизны траектории из формулы для нормального ускорения можем найти для любого момента времени, для любой точки траектории:

Если учесть, что модуль скорости v определяется формулой (10), то и радиус кривизны для произвольного момента времени (произвольной точки траектории) будет иметь достаточно громоздкий вид.

Ограничимся нахождением R по формуле (15) в характерных точках траектории.

В начальный момент времени (t = 0), как следует из (10), v = v0

R = v02 cosα . g

Задача решена.

18

2. ОСНОВНОЕ УРАВНЕНИЕ ДИНАМИКИ ТОЧКИ

Целью динамики является изучение движения тела в зависимости от взаимодействия с другими телами.

Основу динамики составляют законы Ньютона. В динамике выделяют две основные задачи:

−найти, как будет двигаться тело, если известны действующие на него силы и заданы начальные условия;

−найти силы, действующие на тело, если известен закон (законы) его движения.

В тех случаях, когда тело движется поступательно или когда его размеры можно считать малыми по сравнению с характерным масштабом движения, обе эти задачи могут быть решены с помо-

щью основного уравнения динамики

a = ∑F , m

где a – ускорение тела, m – его масса, ∑F – векторная сумма

сил, приложенных к телу. Заметим, что это уравнение справедливо только в инерциальных системах отсчета.

Приступая к решению задач необходимо:

Проработать теоретический материал по теме «Динамика материальной точки» по учебным пособиям из списка рекомендуемой литературы.

Ответить на следующие вопросы:

1.Что является предметом динамики? Каковы основные задачи динамики?

2.Как вы понимаете II закон Ньютона и его роль как основного уравнения динамики точки?

3.Что такое сила? Какие силы Вам известны, какова их приро-

да?

4.Что такое инерциальные и неинерциальные системы отсчета? Для каких систем справедливы законы Ньютона?

Задачи, в которых по заданным силам требуется найти закон движения тела или, по крайней мере, ускорение, предлагается решать по следующей схеме.

19

1. Провести анализ условия задачи.

Выделить из всех тел системы именно то тело или несколько тел, движение которых нас интересует.

Так как II закон Ньютона по смыслу своему применим только к описанию движения материальной точки, то его следует записать для каждого выделенного тела – материальной точки, включив сумму действующих на это тело сил и неизвестные силы реакции со стороны других тел системы (натяжения нитей, реакции опор, силы трения и т.п.).

Сделать чертеж. Нанести на него силы, действующие на выделенные тела.

2. Записать II закон Ньютона.

Ускорение и силы являются величинами векторными. Именно как векторы они и должны быть введены в основное уравнение динамики. Но поскольку для определения вектора необходимо найти его проекции, то в ходе решения задачи следует перейти от векторной записи II закона Ньютона к скалярной.

3. Выбрать систему координат и перейти к записи основного

уравнения в проекциях на координатные оси.

Поскольку II закон Ньютона справедлив только в инерциальных системах, то оси координат надо связывать с телами, которые в условиях задачи можно считать неподвижными или движущимися равномерно и прямолинейно. Направления осей следует выбирать так, чтобы при проектировании векторного уравнения на координатные направления получить как можно более простые выражения. Если точка движется по криволинейной траектории, в частности, по окружности, удобно пользоваться естественными осями –

(τ,n,b).

Рекомендуется при переходе к скалярной записи уравнений проекции неизвестных векторных величин (например, ускорений, иногда сил трения и др.) брать с положительным знаком; их истинный знак определится видом окончательного ответа.

4. Составить полную (замкнутую) систему уравнений.

Если в задаче рассматриваются два и более движущихся тела, то число уравнений динамики, записанных в проекциях, как правило, оказывается меньше числа входящих в них неизвестных. Чтобы замкнуть систему, надо воспользоваться, прежде всего, III законом

20