3-й семестр / Экзамен - Пример билета с решением

МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА» ИИТ ВМ2	Экзаменационный билет №0 Дисциплина: Математический анализ Курс 2 Семестр 3	Утверждено на заседании кафедры (протокол №5 от «_18_»__12___2017г.) Заведующий кафедрой Чекалкин Н.C. 2017-2018 учебный год

Решение

начинаем думать

1. это числовой ряд с положительными членами,

НЕЛЬЗЯ говорить «положительный ряд»

2. «плохое» у этого ряда это , но при аргумент тангенса стремится к нулю

по таблице эквивалентности

таблицу эквивалентностей бесконечно малых функций нужно выучить или печалька((((((((((((((((((((((((((((((((((((((((((((((((((((((

пробуем предельный признак сравнения

для сравнения нам нужен ряд

сходимость которого можно узнать если сравним его с рядом

3.следовательно применяем предельный признак сравнения, сравниваем

ряды ведут себя одинаково и в нашем случае сходятся

начинаем думать

1. это числовой знакочередующийся ряд

НЕЛЬЗЯ к этому ряду применять признаки сходимости для рядов с положительными членами

2. составим ряд из модулей и оценим его сходимость

пробуем предельный признак сравнения, для сравнения нам нужен ряд

3. следовательно, применяем предельный признак сравнения

ряды ведут себя одинаково и в нашем случае сходятся

т.е. ряд из модулей сходится и следовательно, исходный ряд сходится абсолютно.

( по теореме: если сходится ряд составленный из модулей , причем абсолютно.)

Теорему лучше выучить

начинаем думать

1. это степенной ряд, для нахождения области сходимости воспользуемся признаком Даламбера ( для числового ряда с положительными членами), поэтому появляются модули.

так как мы ищем область сходимости степенного ряда, т. е. такие значения при которых ряд сходится, по признаку Даламбера получаем

таким образом, получаем, что радиус сходимости равен 5

2. осталось проверить ряд на сходимость в концах области или в точках

при получаем числовой ряд с положительными членами

при получаем числовой знакочередующийся ряд

начнем с числовой ряд с положительными членами

ряды ведут себя одинаково и в нашем случае расходятся

Рассмотрим знакочередующийся ряд, получаемый из степенного ряда при

Проверим абсолютную сходимость данного знакочередующегося ряда. Для этого составим ряд из модулей

про этот ряд мы знаем, что он расходится, следовательно у знакочередующегося ряда

нет абсолютной сходимости.

Исследуем, сходится ли данный ряд условно, для этого применим признак Лейбница, проверяем выполнение двух условий:

следовательно, по признаку Лейбница ряд сходится. Учитывая, что ряд из модулей расходится, то знакочередующийся ряд, получаемый из степенного ряда при

начинаем думать

1.

значит нужно получить ряд и в степенях которого, присутствует

Сделаем замену

Для функции воспользуемся разложением в рад Маклорена

Разложение функций

в ряд Маклорена все таки стоит выучить

в роли «y» возьмем комплекс

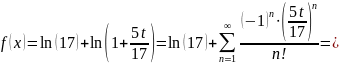
Найдем область сходимости данного ряда

учитывая, что

получим

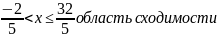
Сделаем замену , получим уравнение

Находим его корни , уравнение распалось на два уравнения

Решаем каждое уравнение:

Необходимо выучить функцию: логарифм от комплексного числа

Знать все три вида записи этой функции

Учитывая, что преобразуем функцию к виду

Выделим действительную часть и мнимую часть функции .

Обратим внимание, что функции являются действительными функциями от двух переменных

Проверим выполнение условий Коши-Римана,

которые нужно выучить или печалька((((((((((((((((((((((((((((((((((((((((((((((((((((((

Выполняться должны оба равенства

как видно, первое условие не выполняется и следовательно,

функция не аналитична

1. приравниваем к нулю знаменатель, чтобы найти особые точки:

2. определим их тип:

Вычислим предел при стремящимся, к особой точке

определяем тип точки

определяем тип точки

Считаем вычет в полюсе первого порядка

Нарисуем границы области .

1. приравниваем к нулю знаменатель, чтобы найти особые точки:

Особой точкой является точка , она входит в область ограниченную кругом.

2. интеграл по основной теореме о вычетах равен 2 умноженное на сумму вычетов в особых точках находящихся в области ограниченной кругом

следовательно, необходимо посчитать вычет в особой точке, лежащей в внутри круга, т.е. в точке

Для этого нужно определить тип особой точки

Так как выражение стоит под знаком элементарной функции, ( под синусом) , то скорее всего это существенно особая точка. Проверим это, разложив подъинтегральную функцию в ряд Лорана. Для этого воспользуемся таблицей стандартных разложений в ряд Маклорена.

Все таки придётся это выучить!!!!!!!

Как видно, главная часть ряда бесконечна, т.е. содержит бесконечное количество слагаемых, следовательно, особая точка является существенно особой точкой.

вычет в особой точке равен коэффициенту, стоящему при или

Тот, кто это сможет понять и выучить, тот может перейти на новый уровень

«я сдал матан!)))»

Дерзайте!)))

«Это невозможно!» - сказала Причина. Это безрассудство!» - заметил Опыт. «Это бесполезно!» - отрезала Гордость. «Попробуй…» - шепнула Мечта.