Набор лекций по Выч. математике ч 4

Наиболее часто в САПР используются разновидности метода сеток:

- МКЭ(метод конечных элементов);

- МКР(метод конечных разностей);

Они отличаются на этапах 1 и 2. Третий этап практически совпадает.

МКЭ(метод конечных элементов).

В математическом отношении является вариационно-разностным. Строгое доказательство устойчивости, сходимости, точности – часто непростая проблема для МКЭ. И поэтому нередко применяется без строго математического обоснования, однако правильность подтверждается точными решениями.

Основные преимущества: доступность, простота понимания, применимость для задач с производственной формой области, возможность создания на его основе универсальных программ для ЭВМ.

Алгоритм МКЭ состоит из следующих этапов

1. Разбиение области на элементы. Элемент – часто треугольник. Разбиение обычно начинают от границы области. Размеры элементов могут отличаться. Затем узлы нумеруются. При нумерации узлов предпочтителен способ, обеспечивающий минимальную разность между номерами узлов в каждом отдельном элементе. Дело тут вот в чем. Мы говорили, что на конечном этапе метода сеток решается система линейных алгебраических уравнений.

Матрица коэффициентов такой системы при применении МКЭ является разреженной, то есть все элементы, кроме близко расположенных к главной диагонали равны нулю. Чем уже ширина L ленты ненулевых элементов, тем меньше нужна _____ для их запоминания и быстрее идет счет. Оказывается L = N+1, где N – максимальная разность между номерами узлов для отдельного элемента.

В случае нашей нумерации N = 14. Можно пронумеровать по другому и получить N = 5. В этом случае сокращается в 3 раза необходимый объем оперативной памяти.

При наличии большого количества элементов (например, нескольких тысяч) задача ручного разбиения и нумерации становится весьма трудоемкой. Поэтому в последнее время стали разрабатываться программы автоматического разбиения и нумерации, которые например минимизируют ширину L.

2) этап. Определение аппроксимирующей функции. Искомая непрерывная функция аппроксимируется кусочно – непрерывной, определенной на множестве конечных элементов. Важным аспектом МКЭ является то, что для элементов одного и того же типа может быть выбрана одна и та же аппроксимирующая функция. Далее она может использоваться в различных краевых задачах, в которых используются элементы данного типа.

Чаще всего в качестве аппроксимирующей функции используются полином(в этом глубокий смысл!- ряд Тейлора). Коэффициенты полинома выражают через узловые значения функции и координаты узлов:

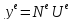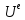лучше = NU

Чтобы понять как вводится аппроксимирующая функция и как она используется для выражения искомой функции через ее узловые значения. Рассмотрим два частных случая.

А) – случай. Одномерная область, то есть некоторая искомая функция _ зависит только от одной переменной x. Отметим, что конечной задачей метода МКЭ является определение узловых значений функции _, но для данного этапа будем считать, что узловые значения нам известны.

По длине элемента (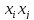) значение функции φ аппроксимируем полином первого порядка

φ = 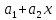(1.19)

Определим 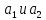, считая что 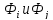– известны.

Учтем, что

φ = 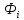при x =

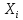
φ = 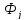при x = (1.20)

Подставив (1.20) в (1.19) получим:

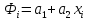
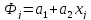(1.21)

Отсюда находим:

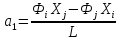
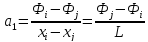
Подставим теперь найденные выражения для 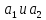в аппроксимационный полином:

φ =

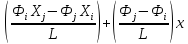
преобразуем:

φ =

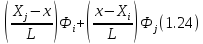
– называются коэффициентами формы.

С их учетом имеем

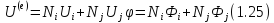
Или в матричной форме:

φ = NФ

где N =

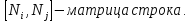
Ф =

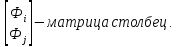
Коэффициенты формы обладают свойством: коэффициенты с номером i равны 1 в узле с номером i и равны 0 во всех других узлах.

Б) Двумерный случай. Покажем, что и в этом случае мы приходим к уравнению в матричной форме φ = NФ, которое связывает значение непрерывной функции φ с ее дискретными значениями в узлах сетки. При этом коэффициенты формы N зависят от текущих координат x и у. Если x и у совпадают с координатами узлов мы получаем значение φ в узлах, а если нет, то между узлами.

Полином, аппроксимирующий непрерывную функцию φ элементарного треугольника имеет вид

φ=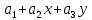

Опять полагаем, что 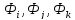и переменные x, y. Для этого опять составим систему уравнений, в которых слева значения φ в узлах элемента, а справа подставляем координаты узлов.

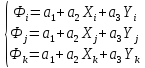
Как и ранее находим из этой системы коэффициенты 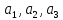, подставляем их в полином аппроксимации и переходя к коэффициентам формы N получим:

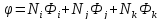; φ = NФ (1.29)

где

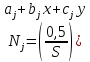
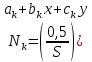
Где S – площадь элемента.

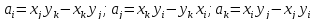
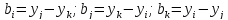
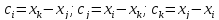
Аналогично могут быть рассчитаны функции для других типов элементов.

3)этап. Объединение конечных элементов в ансамбль.

В результате этого этапа мы приходим к системе уравнений (алгебраических), которая получается если мы рассмотрим одновременно уравнения, полученные для каждого из элементов разбиения. Эта система позволяет при известных узловых значениях искомой функции – получить значение искомой функции в любой точке области.

Эти уравнения нетрудно получить, если мы заменим в уравнениях (1.25) и (1.29) индексы i, j, k на конкретные номера узлов сетки.

Рассмотрим опять одномерный случай. Функция отдельного элемента определена уравнением (1.25). Между номерами узлов каждого элемента и их симв _______ i, j можно написать следующее соответствие.

Элемент 1 i = 1; j = 2;

Элемент 2 i = 2; j = 3;

Элемент 3 i = 3; j = 4;

Элемент 4 i = 4; j = 5;

Элемент 5 i = 5; j = 6;

Подставим эти номера в (1.25) получим:

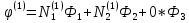
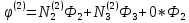
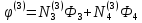
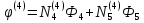
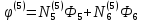
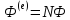
Естественно, что в выражениях для 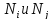также надо подставить глобальные номера узлов, например

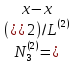
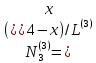
Для двумерного случая: Пусть имеем область. Напишем соответствие между глобальными номерами узлов и их обозначениями в элементе i, j, k(против часовой стрелки).

Элемент 1 i = 1; j = 2; k = 4;

Элемент 2 i = 2; j = 5; k = 4;

Элемент 3 i = 2; j = 4; k = 5;

Элемент 4 i = 4; j = 6; k = 5;

Подставляя эти номера в (1.29) получим

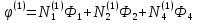
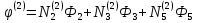
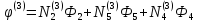(1.34)

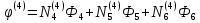
Это сокращенная форма записи системы. В полном расширенном виде эта система имеет вид:

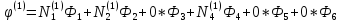
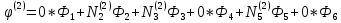
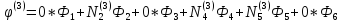
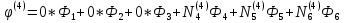
N = .

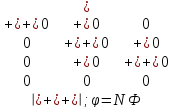В САПР с целью уменьшения объема памяти чаще используют сокращенную форму описания моделей, а именно (1.34). Полная (расширенная) форма имеет преимущества при реализации следующих этапов алгоритма МКЭ.

4) – ый этап. Определение вектора узловых значений функций. Обычно строится некий функционал и находится его минимум. Функционал строится на основе глубокого физического анализа и это не всегда возможно.

1) Пусть такой функционал найден:

F =

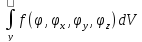
2. F =

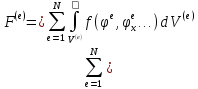
3. Подставляем сюда аппроксимирующие функции: 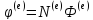и производные:

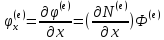
4. Минимизация по вектору Ф функционала

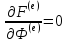(1.17)

5. Суммирование выражений по конечным элементам приводит к системе алгебраических уравнений

KФ = B

6. Найденные узловые значения подставляются в 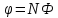, после чего значения φ легко вычисляются в любой точке пространства, в заданной области.

Уравнение теплопроводности описывает процесс распространения теплоты в сплошной среде. В общем случае имеет вид:

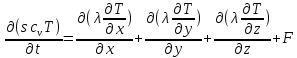
S – плотность среды, - теплоемкость при постоянном объеме, F(x,y,z) – заданная плотность тепловых источников, λ – коэффициент теплопроводности численно равен количеству тепла, которое передается через единицу площади в единицу времени при разности температур между теплоносителями в 1 K = 1 C; α – коэффициент тепло отдачи – количество тепла в единицу времени через единицу поверхности при разности температур между поверхностью и средой теплоносителей в 1 К.

x = 0 |

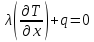
x=e | 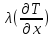+ α(T - 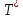) = 0

теплоотдача – теплообмен между теплоносителем и поверхностью твердого тела.

Необходимо рассчитать одномерное температурное поле в однородном стержне. S – поперечное сечение. Конец стержня жестко закреплен и к нему подводится тепловой поток q заданной интенсивности. λ – коэффициент теплопроводности. Даны: α – коэффициент теплообмена, - температура окружающей среды. Вдоль боковой поверхности стержень теплоизолирован.

Температура поля в стержне описывается уравнением теплопроводности

; (y = )

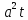Которое в одномерном приближении и стационарном случае имеет вид

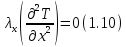
Краевые условия определяются уравнениями

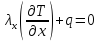при x=0 (1.11a)

при x = L (1.11б)

Искомое температурное поле – непрерывная функция от x.

В МКЭ стержень разбивается произвольным образом на конечные элементы (неравной длины). На каждом элементе T(x) аппроксимируется некоторой линейной зависимостью.

Узловые значения 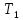÷ 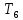в общем случае сначала неизвестны и подлежат определению в МКЭ. После получения модели в виде φ = возникает задача определения узловых значений функций: Ф

Для этого используется несколько методов

1. Метод основанный на вариационной постановке задачи.

В этом методе исходя из физического смысла задачи подбирается некоторый функционал, а затем ищется его минимум. Отметим, что не всегда удается такой функционал найти, это не тривиальная процедура.

Найдем функционал для задачи о стержне:

F = 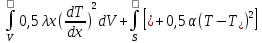dS (1.36)

Для простоты дальнейших вычислений разобъем стержень всего на 2 элемента (в практических случаях этого недостаточно). Тогда

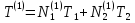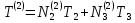; (1.37)

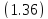представим в виде

F = 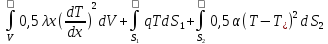(1.38)

где 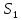и 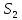- площади сечений стержня, на которых заданы, соответственно, граничные условия (1.11а) и (1.11б).

Рассмотрим вычисление слагаемых в (1.38) в отдельности, учитывая разбиение на 2 элемента

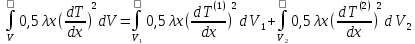(1.39)

Вычислим производные с учетом (1.37) и (1.24):

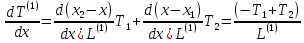
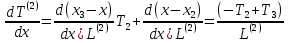(1.40)

Подставим (1.40) в (1.39) и считая, что d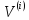 = 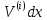получим

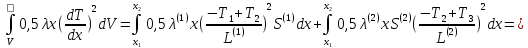
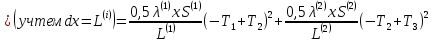(1.41)

Второе и третье слагаемое в (1.38) вычисляются просто, так как подинтегральным функциям соответствуют узловые значения 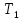и 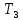.(Ведь 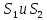– площади на границах)

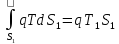
, так как здесь T =

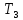
Итак значение функционала F будет равно:

F = 0,5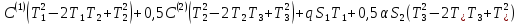 (1.44)

где

Для минимизации функционала необходимо выполнение условия

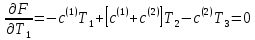
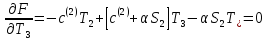
или в матричной форме

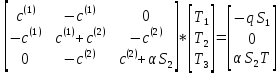(1.45)

что в общем виде вычисляют так

KT = B – матрица жесткости (пошло из строительной механики)

Зная характеристики материала из системы (1.45) можно определить узловые значения

Метод Галеркина

Успешно применяется когда не удается подобрать функционала для минимизации (Например для задач с уравнением Навье - Стокка). Основное преимущество, то что его основой служит исходное дифференциальное уравнение.

Метод Галеркина основан на минимизации ошибки ɛ = L(u) – f приближенного решения и исходного дифференциального уравнения Lφ – f = 0, где L – дифференциальный оператор.

Сочетание метода Галеркина с МКЭ приводит к системе уравнений 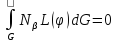при β = i, j, k… где L(φ) – левая часть исходного дифференциального уравнения, описывающего непрерывную функцию φ.

Ошибки метода конечных элементов.

1. Обычные ошибки округления (сходимость, полнота, согласование);

2. Ошибки дискретизации (из за геометрических различий границы области и ее аппроксимации по методу КЭ);

3. Ошибка пробной или базисной функции(из за разности между точным решением и его представлением пробной функцией).

Ошибки дискретизации могут быть уменьшены за счет уменьшения конечных элементов.

Ошибки пробной функции не обязательно уменьшаются с уменьшением элементов, поэтому могут приводить к расходимости.

Пробная функция только тогда даст точное решение, если аппроксимационный полином имеет ∞ степень, но это невозможно.

Критерий ограниченной сходимости. Условием сходимости является представление в виде полного полинома как минимум степени р , где р – наивысший порядок производной, входящей в функционал.