
2-й семестр / Лекция 06
.pdf
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Понятие определенного интеграла
|
Пусть функция |
f (x) определена на отрезке [a,b]. Назовем разбиением |
||||||||||||||||
отрезка [a,b] совокупность точек |
{x0,x1,...,xn}: |
a x0 |
x1 ... xn |
b. |
||||||||||||||
Точки xk |
|
будем называть точками разбиения. |
В каждом из полученных |
|||||||||||||||
отрезков разбиения [xk ,xk 1] |
выберем произвольную точку k . Символом |
|||||||||||||||||
x |
обозначим |
разность |
|
|
= |
− |
( |
т.е. |
|
– |
длина |
отрезка |
||||||
разбиенияk |
). Образуем сумму |
) |
|
|
|
= |
|
( ) |
|
|||||||||
= |
Эту( , |
|
) = ( |
) |
|
+ ( |
|
+...+ |
( |
|
) |
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
сумму называют интегральной суммой (для) |
функции |
f (x) |
на |
||||||||||||
отрезке [a,b], соответствующей данному разбиению |
|
отрезка |
[a,b] и |
|||||||||||||||
данному выбору промежуточных точек k . |
|
|
|
|
|
|
|
|
|
|||||||||
|
Для того чтобы выяснить геометрический смысл интегральной суммы |
|||||||||||||||||
f , изобразим график функции y f (x) на отрезке [a,b] |
(рис. 1). |
|
|
|||||||||||||||
Y |
|
|
f ( n 1) |
C |
|
f ( 1) |
|
|
f ( 0) |
|
|
D |
|
|
A |
B |
X |
0 a x0 x1 x2 |
xn 1 xn b |
|
|
|
|
Рис. 1. |
|
Ясно, что |
– это сумма площадей прямоугольников с основаниями |
|
x0, |
x1, …, xn 1 и высотами |
f ( 0), f ( 1),…, f ( n 1) соответственно |
|
(рис. |
1 сделан |
для случая, когда |
f (x) 0). Очевидно также, что f |
представляет собой приближенное значение площади криволинейной трапеции ABCD (рис. 1), и это приближенное значение тем точнее, чем
«мельче» разбиение отрезка [a,b] |
точками x0,x1,..., xn . При этом площадь k |
|||||||||
-го прямоугольника на рис. 1 равна |
f ( k ) xk . |
|
|
|
|
|||||
Обозначим |
через |
d |
длину наибольшего |
отрезка |
разбиения, |
т.е. |
||||
d max xk . Число d назовем мелкостью разбиения отрезка [a,b]. |
|
|||||||||
0 k n 1 |
|
|
|
|
|
|
|
|
|
|
Определение. |
Число |
I называется пределом |
интегральных |
сумм |
||||||
|
0, |
|
если |
0 |
0, что для любого разбиения |
, у |
||||
которого( , ) приdd |
, |
выполняется |
неравенство |
| |
( , |
) − | < |
при |
|||
произвольном выборе промежуточных точек k .

Функция f (x) называется интегрируемой (по Риману) на отрезке [ , ], если существует конечный предел
lim ( , ) = .
→
При этом число I называется определенным интегралом от функции f (x) по отрезку [a,b] и обозначается символом
b
I f (x)dx.
a
Числа a и b называют нижним и верхним пределами интегрирования, f (x) –
подынтегральной функцией, а x – переменной интегрирования.
Замечание. В отличие от неопределенного интеграла, определенный интеграл представляет собой число, а не функцию.
Если интеграл существует, то это число определяется однозначно и зависит только от вида функции f (x) и от чисел a и b.
Отсюда, в частности, следует, что определенный интеграл не зависит от выбора обозначения для переменной интегрирования:
b b b
f (x)dx f (t)dt f (u)du и т.д.
a a a
Вычисление определенного интеграла в соответствии с приведенным определением связано с трудностями и громоздкими подсчетами. Поэтому чаще используют другие подходы, о которых будет говориться ниже.
Пусть |
функция |
f (x) |
является интегрируемой на |
отрезке |
[a,b] |
функцией. |
В этом |
случае |
будем писать f (x) L[a,b]. |
Здесь |
L[a,b] |
обозначает множество всех интегрируемых на [a,b] функций.
Свойства определенного интеграла
Сначала расширим понятие определенного интеграла. В определении интеграла мы считали, что a b. Распространим это определение на случаи a b и a b, полагая
∫ ( ) = 0 и ∫ ( ) = − ∫ ( )
1) Аддитивность интеграла. Для любых чисел a,b,c имеет место равенство
∫ ( ) = ∫ ( ) +∫ ( ) .
(Предполагается, что интегралы, входящие в эту формулу, существуют.)
Суть доказанного свойства состоит в том, что определенный интеграл по всему отрезку равен сумме интегралов по его частям.
Линейность интеграла. |
Если |
|
|
|
|
|
|
( |
) [ |
, |
], |
|
|
|||||||
любых2) , R функция |
|
|
|
|
|
f (x) |
|
L[a ,b]. |
и |
то для |
||||||||||
|
|
равенство |
) |
|
[ , ] |
|
|
|
|
|
|
|
|
|||||||
При этом справедливо ( |
)+ |
|
|
( |
|
|
|
|
|
|
|
|
|
|||||||
В частности,∫ |
( ) + |
( ) |
|
= |
|
∫ |
) |
( ) |
+ |
∫ |
( ) . |
|
|
|
|
|||||
∫ |
( ) |
= |
∫ |
|
|
( |
|
|
|
(при(при0), |
|
|
|
|||||||
∫ ( ) + ( ) = ∫ ( ) + ∫ ( ) |
|
|
|
= = 1) |
|
|
||||||||||||||
|
[ |
, |
|
) |
||||||||||||||||
для 3)x [a,b], то |
|
|
|
|
Если |
( |
), ( ) |
] и |
( |
) ≤ ( |
||||||||||
Монотонность интеграла. |
|
≤ ∫ |
|
( |
) . |
|
|
|
|
|
|
|
|
|||||||
|
|
∫ |
( |
) |
|
|
|
|
|
|
|
|
|
|
||||||
В частности, если |
( ) ≥ 0, то ∫ |
|
( ) |
|
≥ 0. |
|
|
|
|
|
|
|
|
|||||||
4) Оценки интеграла. Если |
( |
) |
[ |
|
, |
] и [ |
, |
]: |
≤ |
( |
)≤ |
, |
||||||||
то справедливы неравенства |
|
|
|
|||||||||||||||||
|
( − ) ≤ ∫ ( ) |
|
|
≤ ( − ). |
|
|
|
|
|
|
||||||||||
|
Теорема о среднем значении |
|
|
|
|
|
|
|
||||||||||||
Если функция f (x) |
непрерывна на отрезке |
[a, |
b] |
, |
то существует |
|||||||||||||||
число [ , ] такое, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∫( ) = (с)( − ).
Теорема о среднем имеет простой геометрический смысл: существует точка [ , ] такая, что площадь криволинейной трапеции ABCD равна площади прямоугольника ABMK , имеющего высоту f ( ) и основание b a
Y |
|
|
|
C |
|
|
|
|
|
f ( ) |
K |
|
|
M |
|
D |
|
|
|
|
A |
|
|
B |
O |
a |
|
b |
X |
Интеграл с переменным верхним пределом
Сейчас будет получена основная формула интегрального исчисления, которая устанавливает связь между понятиями определенного интеграла и неопределенного, а точнее, первообразной.
До сих пор мы рассматривали определенный интеграл с постоянными пределами интегрирования a и b. Очевидно, что при изменении одного из пределов (например, верхнего) величина интеграла будет изменяться.
Рассмотрим этот вопрос подробнее. Если |
f L[a,b], |
то f (x) |
интегрируема по любой части этого отрезка, |
и поэтому |
x [a,b] |
существует интеграл
x
(x) f (t)dt,
a
называемый интегралом с переменным верхним пределом.
Значение функции (x) раскрывает следующая теорема.
Теорема о дифференцируемости определенного интеграла по переменному пределу. Если функция f (x) непрерывна на отрезке [a, b],
x
то функция (x) f (t)dt дифференцируема в любой внутренней точке x
a
этого отрезка (a x b), причем справедливо равенство |
|
|||||||
( ) |
= |
( ) |
, |
т.е. ( |
∫ ( ) |
|
)′ = |
. |
|
|
|
|
( ) |
||||
Имеет место аналогичное равенство:
(∫ ( ) )′ = − ( )

Доказательство. Зафиксируем любое значение |
x (a,b) и придадим |
||||||
ему приращение |
x 0 столь малое, |
чтобы точка |
x x |
лежала внутри |
|||
отрезка [a,b], |
|
a x x b. Тогда |
|
x x |
|||
т.е. |
(x x) |
f (t)dt. Найдем |
|||||
производную функции (x). Имеем |
|
|
a |
|
|||
|
|
|
|
||||
|
|
|
|
x x |
x |
|
|
(x x) (x) |
|
f (t)dt f (t)dt |
|||||
|
|
|
|
a |
a |
|
|
|
x |
|
x x |
x |
x x |
|
|
|
f (t)dt |
f (t)dt f (t)dt f (t)dt. |
|
||||
|
a |
|
x |
a |
x |
|
|
Теперь к полученному интегралу применим теорему о среднем значении:
x x
f (t)dt f (c) x,
x
где c [x,x x], если x 0 (или c [x x,x], если x 0). Отсюда
f (c).x
Поскольку функция f (x) непрерывна на [a,b] и c x при x 0, то
lim |
f (c) f (x). |
||
x 0 |
|
||
Поэтому |
|
|
|
|
lim f (c) f (x). |
||
|
|||
(x) lim |
x |
||
x 0 |
c x |
||
Теорема доказана. |
|
|
|
Замечание. Таким образом, установлено следующее утверждение: |
|||
Любая непрерывная на отрезке [a,b] |
функция f (x) имеет на этом отрезке |
||
|
|
x |
|
первообразную, а именно, функцию (x) f (t)dt.
a
Поскольку всякая другая первообразная для функции f (x) может отличаться от указанной функции (x) только на постоянную, то получена связь между неопределенным и определенным интегралами в виде:
x
f (x)dx f (t)dt C,
a
где C – произвольная постоянная.
Формула Ньютона-Лейбница
Последняя теорема не только указывает на связь между понятиями неопределенного и определенного интеграла, но и дает практический способ вычисления определенных интегралов в случае, когда подынтегральная функция непрерывна.

Если функция f (x) непрерывна на отрезке [a, b], то справедлива следующая формула
b
f (x)dx F(b) F(a),
a
где F(x) – произвольная первообразная для функции f (x).
Эта формула называется формулой Ньютона-Лейбница.
Доказательство. Поскольку функция f (x) непрерывна на отрезке
|
|
|
b |
|
|
[a,b], то она интегрируема на нем и, значит, существует f (x)dx. |
|
||||
|
|
f (x) |
a |
[a,b] |
|
Далее, в силу непрерывности функции |
на отрезке |
у нее на |
|||
этом отрезке существует первообразная (см. последнее Замечание). |
|
||||
Более того, в последней |
теореме |
было |
доказано, |
что |
функция |
x |
из первообразных для функции f (x); |
||||
(x) f (t)dt является одной |
|||||
a
следовательно, для любой первообразной F(x) имеем
(x) F(x) C.
Отметим, что это равенство выполняется тождественно, т.е. x [a,b].
|
|
a |
|
(a) F(a) C , то |
C F(a). |
Поскольку |
(a) f (t)dt 0 |
и |
|||
|
|
a |
|
|
|
Следовательно, |
|
(x) F(x) F(a), |
в |
частности, (b) F(b) F(a). Но |
|
b |
b |
|
|
|
|
(b) f (t)dt f (x)dx, откуда и получаем формулу Ньютона-Лейбница.
a a
Разность F(b) F(a) принято условно записывать в виде F(x)ba ,
поэтому формула Ньютона-Лейбница в общепринятой краткой записи выглядит следующим образом:
∫( ) = ( )| .
Методы вычисления определенных интегралов
Поскольку формула Ньютона-Лейбница сводит задачу вычисления определенного интеграла от непрерывной функции к нахождению первообразной, то методы вычисления неопределенных интегралов сводятся к вычислению определенных интегралов.

Два основных метода нахождения неопределенных интегралов: метод замены переменной и интегрирование по частям - с учетом специфики определенных интегралов приобретают следующие формы.
Замена переменной в определенном интеграле. Пусть
1) |
функция f (x) непрерывна на [a, b], а функция |
( ) непрерывно |
|
дифференцируема на [a, b]; |
|
2) |
a (t) для t [ , ]; |
|
3) |
( ) a, ( ) b. |
|
Тогда справедливо равенство:
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
f (x)dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
f ( (t)) (t)dt. |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Для доказательства этого равенства достаточно применить к обеим его |
|||||||||||||||||||||||||||||||||||||
частям формулу Ньютона-Лейбница и учесть, что если F(x) |
первообразная |
||||||||||||||||||||||||||||||||||||||
для |
|
f (x), то функция (t) F( (t)) будет первообразной для |
f ( (t)) (t). |
||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
x sint |
|
|
|
/2 |
|
|
|
|
|
|
|
|
|
1 |
/2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
1 x2 dx |
|
|
|
|
cos2 tdt |
|
||||||||||||||||||||||||||||
|
|
Пример. |
|
|
|
|
|
|
|
(1 cos2t)dt |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
dx costdt |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
2 |
0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
sin2t |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
0 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
4 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Интегрирование по частям для определенного интеграла. Пусть |
|||||||||||||||||||||||||||||||||||||
функции |
( ) и |
|
( ) |
непрерывно дифференцируемы на [a, b]. Тогда: |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
budv uv |
|
b b vdu. |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Справедливость |
|
этой |
|
|
|
|
формулы |
|
следует |
из равенства |
||||||||||||||||||||||||||
(uv) |
|
|
|
|
и применения формулы Ньютона-Лейбница к интегралу от |
||||||||||||||||||||||||||||||||||
|
u v uv |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
, для которой первообразной будет функция uv. |
|||||||||||||||||||||||||||||||||
функции u v uv |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
u x, dv |
e |
x |
dxx |
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Пример. xex dx |
|
|
|
|
|
|
xex |
|
0 |
ex dx |
|
||||||||||||||||||||||||||
|
|
|
du dx, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
v e |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
2e2 0 ex |
|
2 2e2 e2 1 e2 1. |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Определенные интегралы имеют многочисленные приложения в самых разнообразных задачах. Здесь мы ограничимся рассмотрением некоторых геометрических приложений.
1. Вычисление площади плоской области
а) Площадь криволинейной трапеции
Площадь S криволинейной трапеции, ограниченной сверху графиком функции y f (x), снизу – отрезком с оси x, а по бокам – прямыми x a и x b, вычисляется по формуле
= ∫ ( ) .
Обоснование этой формулы было дано при введении понятия определенного интеграла.
Если график функции расположен ниже оси Ох, т.е. ( ) < 0, то площадь трапеции имеет знак “-“, а если график расположен выше оси Ох, т.е. ( ) <0, то площадь имеет знак “+”.
Вболее общем случае, как на следующем рисунке,
++
-
определенный интеграл от ( ) на [a, b] равен сумме площадей частей изображенной области, которые лежат выше оси Ох, и минус площади тех частей области, которые лежат ниже оси Ох.
Если верхняя граница криволинейной трапеции задана уравнениями в параметрической форме x (t), = ( ) ≥ 0, t , причем ( ) a,( ) b, то произведем формуле площади криволинейной трапеции замену переменной, полагая x (t), dx (t)dt.
Тогда получим формулу площади криволинейной трапеции, заданной в параметрическом виде:
= ∫ ( ) ( ) .

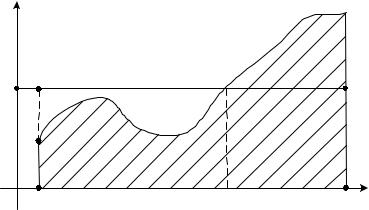
Более общая задача – найти площадь плоской области, ограниченной двумя непрерывными линиями – графиками функций ( ) и ( ) (см. рис.).
Легко понять, что такая площадь находится по следующей формуле:
= ∫ [ ( )− ( )] ,
где – площадь криволинейной плоской области, ограниченной графиками функций у = ( ), у = ( ) таких, что ( ) ≥ ( ) на [a, b], и по бокам
- отрезками прямых = и = .
Пример. Вычислить площадь фигуры, ограниченной эллипсом x acost , y bsint (0 t 2 ).
y b
b



 a
a
0 x
Рис.
Решение. Эллипс симметричен относительно осей координат, поэтому достаточно вычислить площадь части фигуры, находящейся в I четверти Следовательно, искомая площадь равна
0 |
|
|
|
2 |
2 |
2 |
||
S 4 |
dt 4ab sin |
tdt 2ab (1 cos2t)dt |
||||||
bsint(acost) |
|
|||||||
2 |
|
|
|
0 |
|
|
0 |
|
|
|
|
1 |
|
|
2 |
||
|
|
|
||||||
|
|
|
|
|
||||
|
2ab t |
|
sin2t |
|
|
ab. |
||
|
2 |
|
||||||
|
|
|
|
|
0 |
равны (a b R), то получаем |
||
|
|
|
||||||
В частности, если полуоси |
эллипса |
|||||||
известную формулу площади круга R2 .
б) Площадь криволинейного сектора
Пусть кривая задана в полярных координатах уравнением ( ),, причем функция ( ) непрерывна и неотрицательна на отрезке [ , ]. Плоскую фигуру, ограниченную дугой AB этой кривой и двумя лучами, составляющими с полярной осью углы и ( , ),
называют криволинейным сектором (см. рис.).

i
B 


A




















0 |
C |
Рис.
Площадь криволинейного сектора вычисляется по формуле:
|
|
= |
|
∫ |
|
( |
) . |
|
|
|
|
|
Доказательство. |
|
|
отрезок |
|
|
] |
точками |
|||||
Разобьем |
произвольно |
[ , |
|
|||||||||
0 |
1 ... n |
на |
n |
частей, выберем на каждом частичном |
||||||||
отрезке |
[ i , i 1] произвольно |
|
точку |
i |
( i |
i i 1) |
и |
|
построим |
|||
круговые секторы с радиусами ( i ).
В результате получим веерообразную фигуру, площадь которой приближенно равна площади S криволинейного сектора:
1n 1
S 2i 0 2( i ) i ,
где i i 1 i . В правой части стоит интегральная сумма для искомого интеграла. Так как функция 2( ) непрерывна на отрезке [ , ], то предел
этой суммы при d max { i } 0 существует и равен этому интегралу.
1 i n
С другой стороны, при → 0 указанное приближение будет становиться все точнее и точнее, так что записанная интегральная сумма будет стремиться к площади криволинейного сектора. Таким образом,
1 |
|
n 1 |
1 |
|
|
|
|
S |
|
lim |
2( i ) i |
|
|
2 |
( )d . |
|
2 |
||||||
|
2d 0 |
i 0 |
|
|
|||
Пример. Вычислить площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда: a , где a – положительное число.
