Курсовая по теории игр

Курсовой проект по методам оптимизации.

Студента группы Т9-31, Балашова С.В.

15 декабря 2010 г.

1Введение

Âкурсовом проекте решалась задача оптимизации портфеля инвестиций. Была задана ковариационная матрица эффективности для двух случаев: диагональная и с уче- том ковариционных связей. Построение оптимального портфеля проводилось согласно модели Марковица с разрешением операции short sale и в условиях, когда эта операция запрещена.

2Схема Марковица

Под портфелем инвестиций понимают вектор долей ~x = (x1; : : : ; xn)T инвестиру- емого капитала в объекты инвестирования i = 1; : : : ; n : В проекте рассматривался

случай n = 3 : Ri эффективность вложения капитала в i тый объект инвестирования. Согласно Марковицу для решения задачи оптимального распределения капитала между объектами инвестирования нужно знать ковариационную матрицу W ; Wij = cov(Ri ; Rj) ; i ; j = 1; : : : ; n и вектор m~ = (m1; : : : ; mn)T ; mi ожидаемое среднее значе- ние эффективности i того объекта инвестирования. Портфель характеризуется двумя

критериями - риском портфеля p = p(x) , который нужно минимизировать, и ожидаемым средним значением эффективности портфеля mp = mp(x), которое нужно максимизировать.

2.1Исходные данные(3-й вариант)

W = diag(0;1; 0;15; 0;35) ;

m~ = (1;2; 1;3; 1;5)T ;

r12 = 0;74; r13 = r23 = 0 :

2.2Задача Марковица в условиях "short sale"

Постановка задачи:

:

Это задача квадратичного программирования с ограничениями типа равенств. Для решения этой задачи рассмотрим однокритериальную задачу:

Функция Лагранжа этой задачи имеет вид:

1

Соответствующее значение эффективности портфеля mp = (m;~ ~x ), а дисперсия p2 = (W~x ; ~x ). Далее рассматриваем многокритериальную задачу:

бивается на N промежутков, и для каждого mp = mp + mpi, где i = 1; : : : ; N решается задача минимизации.

Удобно записать задачу в матричной форме:

Запишем функцию Лагранжа этой задачи:

2

2.3 Задача Марковица с запретом "short sale"

Постановка задачи:

>

>

>

: ~ ~x > 0

3

Систему (21) можно решить с помощью метода Гаусса-Зейделя.

При решение методом Гаусса-Зейделя нужно учитывать наше ограничение: u(il+1) = maxfu~(il+1); 0g; i = 1; : : : ; n

u(nl+1+1) = u~(nl+1+1)

И затем определяем ~x и mp

Далее рассматриваем многокритериальную задачу:

3Результат

Все графики и листинг программы, написанный на C++, представленны в Приложении.

Для случая запрета "short sale"не удалось реализовать алгоритм, так как матрица из (19) для случая коррелированной и некоррелированной матрица W имеют следую-

щий соответствено вид:

Собственные числа для них, посчитанные в Mathcad 14, будут равны соответсвенно:

Что говорит нам о том, что матрица c в обоих случаях не является положительно

определенной, и следовательно метод Гаусса-Зейделя к ней не может быть применен. Так же в обоих случаях не удалось найти c 1.

4

4Вывод

1.Учет корреляций в случае разрешения операции "short sale"приводит к росту рисков в области малых математических ожиданий.

2.Рост эффективности инвестиционного портфеля приводит к ускорению роста рисков.

5

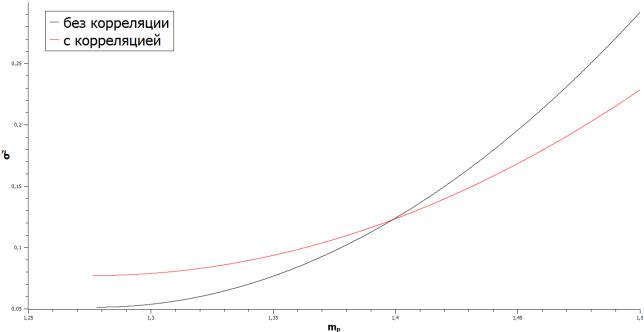
Приложение

Рис. 1: Зависимость риска от эффективности портфеля в условиях "Short Sale"

#include <fstream> #include "matrix.h" #include "vector.h" using namespace std;

void Short_Sale(matrix W, vector m); void Markowitz(matrix W, vector m);

vector Seidel(matrix A, vector b, float eps); int main()

{

//зада¼м ковариационную матрицу matrix W(3,3);

W.a[0][0]=0.1; W.a[0][1]=0; W.a[0][2]=0; W.a[1][0]=0; W.a[1][1]=0.15; W.a[1][2]=0; W.a[2][0]=0; W.a[2][1]=0; W.a[2][2]=0.35;

//задаем вектор эффективностей vector m(3);

m.x[0]=1.2; m.x[1]=1.3; m.x[2]=1.5; Short_Sale(W,m);

Markowitz(W,m);

cin.get(); return 0;

}

6

void Short_Sale(matrix W, vector m)

{

//решение задачи в постановке Short Sale vector one(m.n);

for (int i=0; i<one.n; i++) one.x[i]=1;

float m_p,S; vector x(m.n); matrix A(2,3);

A.a[0][0]=1; A.a[0][1]=1; A.a[0][2]=1; A.a[1][0]=m.x[0]; A.a[1][1]=m.x[1]; A.a[1][2]=m.x[2]; vector f(2);

f.x[0]=1;

//определение максимального значение эффективности портфеля float m_p_max=0;

for (int i=0; i<m.n; i++)

if (m.x[i]>m_p_max) m_p_max=m.x[i]; //решение однокритериальной задачи (2) x=(Invert(W)*one)/((Invert(W)*one)*one); m_p=x*m;

S=(W*x)*x; ofstream fout;

fout.open("short sale.txt");

fout <<"Expected valuet\tVariance\n"; fout << m_p <<"\t"<< S <<"\n"; //решение многокритеривальной задачи (8) //зада¼м число разбиений

int N=1000; float c;

c=(m_p_max-m_p)/N;

for (int i=1; i<=N; i++)

{

m_p=m_p+c; f.x[1]=m_p;

x=Invert(W)*Transpose(A)*Invert(A*Invert(W)*Transpose(A))*f;

S=(W*x)*x;

fout << m_p <<"\t"<< S <<"\n";

}

fout.close();

}

void Markowitz(matrix W, vector m)

{

//решение задачи в постановки запрета Short Sale float m_p,S,m_p_max;

vector x(m.n);

7

//определение максимального значение эффективности портфеля m_p_max=0;

for (int i=0; i<m.n; i++)

if (m.x[i]>m_p_max) m_p_max=m.x[i]; //решение однокритериальной задачи (14) matrix A(4,3);

A.a[0][0]=1; A.a[0][1]=0; A.a[0][2]=0;

A.a[1][0]=0; A.a[1][1]=1; A.a[1][2]=0;

A.a[2][0]=0; A.a[2][1]=0; A.a[2][2]=1;

A.a[3][0]=1; A.a[3][1]=1; A.a[3][2]=1; vector b(4);

b.x[0]=0; b.x[1]=0; b.x[2]=0; b.x[3]=1; matrix c(4,4); c=A*Invert(W)*Transpose(A);

vector U(c.m); U=Seidel(c,b,0.1);

//далее программа зависает, т.к. метод Зейделя рассходится

}

vector Seidel(matrix A, vector b, float eps)

{

//решение СЛАУ методом Гаусса-Зейделя vector x(b.n);

for (int i=0; i<x.n; i++) x.x[i]=0;

float c; do

{

for(int i=0; i<x.n; i++)

{

c=0;

for (int j=0; j<x.n; j++)

if (j!=i) c=c+A.a[i][j]*x.x[j]; x.x[i]=(b.x[i]-c)/A.a[i][i];

}

}

while(norm(A*x-b)>eps); return x;

}

8