ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ВОСТОЧНО-СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

ЭКОЛОГО-ГУМАНИТАРНЫЙ ФАКУЛЬТЕТ

Кафедра прикладной математики

Курсовая работа

по дисциплине «Численные методы»

Тема: «Метод пристрелки»

Выполнил:

ст. гр.743

Руководитель:

_____________Назарова Л.И.

Дата защиты:_______Оценка_______

Улан-Удэ

2007

ВОСТОЧНО-СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

_________________________________________________________________

ЭКОЛОГО-ГУМАНИТАРНЫЙ ФАКУЛЬТЕТ

Кафедра прикладной математики

ЗАДАНИЕ

на курсовую работу

Дисциплина: Численные методы_____________________________________

Тема: Метод пристрелки____________________________________________

Исполнитель:_________________________________________

Руководитель: Назарова Л.И.

Краткое содержание работы: Численное решение дифференциальных уравнений

1. Основная часть: Вычисление численных значений методом пристрелки

Сроки выполнения работы по графику:

1. Патентный поиск - ____% к ____ неделе.

2. Обзор литературы - ____% к ____ неделе.

3. Разработка постановки задачи и модели - ____% к ____ неделе.

4. Оформление отчета - ____% к ____ неделе.

5. Защита проекта ___________ недели.

Требования к оформлению:

1. Отчет должен быть представлен в электронной и твердой копиях.

2. Объем отчета должен быть не менее 20 машинописных страниц без учета приложений.

3. Отчет должен быть оформлен по ГОСТу 7.32-81 и подписан у нормоконтролера.

Руководитель работы ________________Назарова Л.И.

Исполнитель____________ Дата выдачи___________________2007г. Аннотация

В данной курсовой работе содержится описание численного решения дифференциальных уравнении высших порядков.

Курсовая работа состоит из основной части и приложения.

В основной части рассмотрены понятия численных решений ОДУ методом пристрелки.

Приложение содержит модуль, написанную на языке Turbo Pasсal, которая реализует численное решение обычных дифференциальных уравнений. И для примера одну программу «метод Рунге-Кутта». Дополнительные программы, находятся на сменном носителе, который прилагается к курсовой работе.

Курсовая работа состоит из 18 листов.

Приложение занимает 7 страниц.

Содержание

1. Введение

2. Основная часть

3. Заключение

4. Список литературы

5. Приложение

Введение

Обыкновенным дифференциальным уравнением (ОДУ) называется уравнение вида:

f( x, y, y`, y``,. . . , y) = 0 ,

где порядок старшей производной к называется порядком ОДУ. ОДУ имеет бесконечно множество решений. Для отыскания конкретного решения требуются дополнительные условия. Эти условия могут быть двух типов:

- Задача Коши с начальными условиями(НУ). Дополнительные условия задаются при одном значении независимой переменной. Например, при x=a заданы значения функции y0, и возможно некоторые производные искомой функции y0`, y0`` и т.д.

- Краевая задача – задача с граничными условиями(ГУ). Дополнительные условия задаются при двух (или более) значениях независимой переменной. Например, x=a задано значение функции ya , при x=b – значение yb.

Методы решения задачи Коши:

- Аппроксимация рядом Тейлора

- Методы Рунге-Кутты

- Методы прогноза и коррекции

Нулевым приближением всех методов решения задачи Коши является метод Эйлера.

Методы решения краевой задачи:

- Методы стрельбы (пристрелки)

- Проекционные методы

- Метод конечных разностей

Далее остановимся более подробно именно на методе стрельбы.

Основная часть

Метод стрельбы - это численный метод, заключающийся в сведении краевой задачи к решению последовательности задач Коши для той же системы дифференциальных уравнений. Рассмотрим его на примере простейшей задачи для системы двух уравнений первого порядка с краевыми условиями достаточно общего вида:

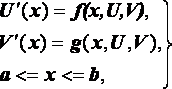
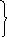(1)

(2)

Выберем произвольно значение , рассмотрим левое краевое условие как алгебраическое уравнение и найдем из него Возьмем значения , в качестве начальных условий задачи Коши для системы (1) и проинтегрируем эту задачу Коши любым численным методом. При этом получим решение , зависящее от , как от параметра.

Значение выбрано так, что найденное решение удовлетворяет левому краевому условию (2). Однако правому краевому условию это решение, скорее всего, не удовлетворяет: при его подстановке левая часть краевого условия в точке b, рассматриваемая как функция параметра

(3)

не обратится в нуль.

Необходимо каким-либо способом менять параметр , пока не подберем такое значение, для которого с требуемой точностью. Таким образом, решение краевой задачи (1) сводится к нахождению корня уравнения

(4)

Простейшим методом его решения является метод дихотомии (деления отрезка пополам). Делают пробные "выстрелы" – расчеты с наудачу выбранными значениями до тех пор, пока среди величин не окажется разных по знаку. Пара таких значений образует "вилку". Деля ее последовательно пополам до получения нужной точности, производим "пристрелку" параметра . Благодаря этому процессу весь метод получил название стрельбы.

Однако нахождение каждого нового значения функции требует численного интегрирования системы (1), то есть достаточно трудоемко.

Поэтому корень уравнения (4) желательно находить более быстрым методом.

Попробуем сделать это методом Ньютона:

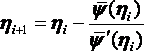(5)

Однако вычисление производной затруднительно и лучше ее заменить разностным отношением

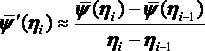(6)

Подставляя (6) в (5), получим итерационную формулу метода секущих:

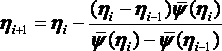(7)

В методе секущих первые два расчета делают с наудачу выбранными близкими значениями и , а следующие значения параметра вычисляют по формуле (7).

Заметим, что этот метод быстро сходится вблизи корня. Сходимость вдали от корня зависит от того, насколько удачно выбрано нулевое приближение.

Рассмотрим теперь линейную краевую задачу, решение которой методом стрельбы особенно просто:

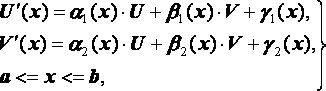(8)

(9)

Воспользуемся известным результатом из теории дифференциальных уравнений: общее решение линейной неоднородной системы равно сумме ее какого-нибудь частного решения и общего решения соответствующей однородной системы.

Найдем частное решение неоднородной системы (8), положив в левом условии (9) . Обозначим это частное решение через и заметим, что .

Рассмотрим теперь соответствующую однородную систему

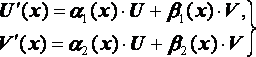
с однородными начальными условиями

Вычислим решение этой задачи Коши и обозначим его через . Рассмотрим функции и . Очевидно, что в точке a эти функции удовлетворяют краевому условию:

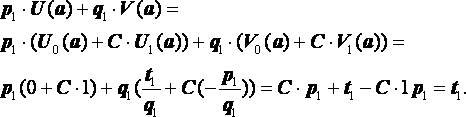
Поэтому общее решение неоднородной задачи Коши, удовлетворяющее левому краевому условию (9) дается следующим однопараметрическим семейством

(10)

Значение параметра C выбираем так, чтобы удовлетворить правому краевому условию (9):

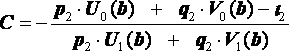. (11)

Искомое решение краевой задачи (8),(9) тогда находится по формуле (11).

Рассмотрим краевую задачу на примере ОДУ второго порядка с граничными условиями у(х = а) = у_а, у(х = Ь) = уъ. Метод стрелбы сводится к замене решения краевой задачи решением последовательности задач Кошии. В начальной точке х = а помимо строго заданного граничными условиями (ГУ) значения функции у_а задается значение производной у'{х = а) = у'_а. После этого про­изводится "выстрел": при сформированных начальных условиях решается задача Коши, вплоть до точки х = b. Там происходит проверка, удалось ли при заложенной производной удовлетворить ГУ в последней точке. Затем задается другое значение производной в точке х = а, снова решается задача Коши, и т.д. Анализируя характер получаемых решений и их зависимости от задаваемого значения производной в начальной точке, находится решение удовлетворяющее одновременно обоим заданным ГУ.

Если исходное ОДУ — линейное, т.е. имеет вид

у" = fi(x)y' + f2(x)y + /з(ж),

то для поиска истинного решения достаточно всего двух "прицелочных выстрелов"(для уравне­ния второго порядка). Действительно, пусть найденные два решения у\(х) и У2(х) да­ют :

yi(x = b) = Pi, у2(х = b) = Р2,

тогда искомым решением является

y(x)=y1(x)*(y(b)-2)/(1-2)+ y2(x)(1-y(b))/(1-2)

Недостатки:

- Большой объем вычислений (для нелинейных ОДУ).

- Жесткость исходной задачи.

Так, например, общее решение ОДУ у'{х) = у(х) — sin(x) + cos(x), имеет вид: у = sin(x) + ехр(х). Частным решением, удовлетворяющим НУ : у(0) = 0, явля­ется у(х) = sin(x). Однако незначительная погрешность в задании НУ приводит к катастрофическому искажению результата. Причем, это связано не с погрешностью расчета, а с расходимостью интегральных кривых ОДУ