8. Достаточное условие непрерывности функции в точке.

Пусть f(x) определена на [a,a+). Функцияf(x) называется непрерывной в точкеасправа, если f(x) =f(а). (то естьf(а+ 0) =f(а)).

Аналогично определяется непрерывность в точке аслева.

Пример:

f(x) = [x].

(рисунок)

 целого n:f(n- 0) =n- 1,f(n+ 0) =n,f(n) =n, то есть,f(n+ 0) =f(n)f(n- 0).

Следовательно , в целочисленных точках эта функция непрерывна только справа. В остальных точках- и справа и слева.

Теорема 3.1

Если f(x) непрерывна в точкеасправа и слева, то она непрерывна в точкеа.

Доказательство:

По условию f(а+ 0) =f(а) иf(а- 0) =f(а).

Отсюда по теореме 2.1(Если в точке a правое и левое предельные значения функции f(x) равны, то в точке a существует предельное значение этой функции, равное указанным односторонним предельным значениям) следует, что f(x) =f(а), а это и означает, чтоf(x) непрерывна в точкеа.

Теорема доказана.

9. Производная обратной функции.

Теорема 4.3.

Пусть функция y=f(x) определена, строго монотонна и непрерывна в некоторой окрестности точкиx₀, дифференцируема в точкеx₀, причём производнаяf '(x₀)0. Тогда в некоторой окрестности точкиу₀(гдеу₀=f(x₀)) существует обратная функцияx=f^-1(y), эта обратная функция дифференцируема в точкеу₀, иf^-1'(y₀)=.

Доказательство:

(рисунок)

Из условий теоремы следует: [a,b]:y=f(x) определена, строго монотонна и непрерывна на [a,b]. причёмa<x₀<b. Поэтому, согласнотеореме 3.5, множеством значенийf(x), рассматриваемой на [a,b], является сегментY= [f(a),f(b)], наYсуществует обратная функцияx=f^-1(y), строго монотонная и непрерывная. При этомy₀(f(a),f(b)). Зададим приращениеy0 аргументу обратной функции в точкеy₀. Обратная функция получит приращениех=f^-1(y₀ +y) -f ^-1(y₀), причемх0 в силу строгой монотонности обратной функции. Рассмотрим равенство:

=.(1)

Пусть y0, тогдах0 в силу непрерывности обратной функции. Но прих0 знаменатель в правой части равенства(1) стремится кf '(x₀), причем по условиюf '(x₀)0. Поэтому приy0 предел правой части равен . Следовательно приy0 существует предел левой части равенства(1), то есть существует производная обратной функции в точкеу₀и она равна :f^-1'(y₀)=.

Теорема доказана.

Примеры:

1). y = sin x, -< x <. sin x f(x), x = arcsin y. arcsinyf^-1(y)x(-,) выполнены все условия теоремы 4.3

2). (arcsiny)' = ===[гдеsin² xy²] =. (arcsinx)' = , -1 <x< 1.

3). y=tgxна -<x<

x = arctg y.  x(-,) выполнены все условия теоремы 4.3

(arctg y)' == cos² x ==; (arctg x)' =.

10. Производная сложной функции.

Рассмотрим сложную функцию: y=f(t), гдеt=(x), то естьy=f((x))F(x).

Теорема 4.4. Пусть функцияt=(x) дифференцируема в точке х₀, а функцияy=f(t) дифференцируема в точкеt₀, гдеt₀ =(х₀). Тогда сложная функцияF(x) =f((x)) дифференцируема в точке х₀, и имеет место формулаF'(х₀) =f'(t₀)'(х₀) =f'((х₀))'(х₀).

Доказательство:

Нужно доказать, что приращение функции y=F(x) =f((x)) в точке х₀ можно представить в виде:y=f'(t₀)'(х₀)x+(x)x, (1), где(x)0 приx0.(0) = 0. Зададим в точке х₀приращение аргумента х, равноеx. Тогда функцияt=(x) получит приращениеt=( х₀ +х) -(х₀). Так какt=(x) дифференцируема в точке х₀ +, тоtможно представить в виде :t='(х₀)x+(x)x. (2), где(x)0 приx0.(0) = 0. Приращениюtсоответствует приращениеy=f(t₀+t) +f'(t₀), функцииy=f(t). Так какy=f(t) дифференцируема в точкеt₀, тоyможно представить в виде:

y=f'(t₀)t+(t)t. (2), где(t)0 приt0.(0) = 0. (3)

Подставляя (2) в (3), получим:

y=f'(t₀ )('(х₀)x+ [f'(t₀)(x) +'(х₀) +(x)]x, где [f'(t₀)(x) +'(х₀) +(x)](x).

Очевидно, что (x)0 прих0,х0.

Тем самым доказано равенство (1), и, значит, теорема 4.4 доказана.

Примеры:

1. y=x^ (- любое вещественное число,x> 0).x^ =e^{ln x} =e^ , гдеt=lnx(lnx(x))

По теореме 4.4 получаем:

(x^)' =(e^)'(lnx)'= (e^)=x^-1. (e^=х^),= х). (x^)' =x^-1.

В частности, если =,()'=x^-1/2=.Если= -1, то= -1x^-2 = -.

Из правил и формул дифференцирования следует, что производная любой элементарной функции снова есть элементарная функция. Иными словами, класс элементарных функций замкнут относительно операции дифференцирования.

2. y = arccos (arctg e^x )

y' = (-sin (arctg e^x))e^x = -tg(arctg e^x)=-.

3. y =[u(x)]^v(x). y =e^vlnu. y = u(x^v)' = e^vlnu.(v ln u)' = u^v(v'ln u + v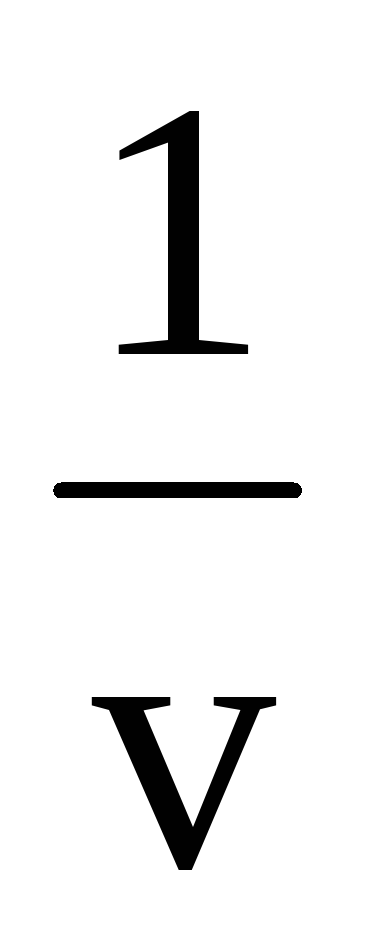u') = u^vln u v' + vu^v-1u'

(u^v)' = (u^v)'+ (u^v)'