Teoria_chisel_i_kriptozashita

К≡ (YВ)ХА (mod97) ≡ 4436 ≡ 75(mod97) ,

К≡ (YА)ХВ (mod97) ≡ 5058 ≡ 75(mod97).

Имея 44 и 50, нарушителю не удастся с легкостью вычислить 75. На рисунке 4 представлен простой протокол, в котором применяются

вычисления в соответствии со схемой Диффи — Хеллмана [9]. Предположим, что пользователь А собирается установить связь с пользователем В и использовать секретный ключ, чтобы зашифровать сообщения, передаваемые с помощью такой связи. Пользователь А может сгенерировать однора-

зовое секретное значение ХА, вычислить значение ΥА и отослать последнее пользователю В. В ответ пользователь В генерирует секретное значение ХВ , вычисляет ΥB и посылает ΥB пользователю А. Оба пользователя теперь могут вычислить их общий ключ. Необходимые открытые значения q и α должны быть известны заранее. Пользователь А может также выбрать эти значения на свое усмотрение и включить их в первое сообщение.

Можно рассмотреть другой пример использования алгоритма Диффи — Хеллмана для группы пользователей локальной сети. В этом случае

каждый пользователь должен сгенерировать секретное значение ХА для

долгосрочного применения и вычислить открытое значение ΥА. Все полученные таким образом открытые значения вместе с открытыми глобальными значениями q и α сохраняются централизованно в некотором каталоге. В любой момент пользователь В может получить доступ у открытому значению пользователя А, вычислить секретный ключ и использовать его для пересылки шифрованного сообщения пользователю А.

Рис. 4. Обмен ключами по схеме Диффи — Хеллмана

Если централизованный каталог надежен, то эта форма коммуникации обеспечивает как конфиденциальность, так и определенную степень аутентификации. Поскольку только пользователи А и В могут определять ключ, другой пользователь не может прочитать сообщение, чем обеспечивается конфиденциальность. Получатель А знает, что только пользователь

51

В мог создать сообщение, используя этот ключ, чем обеспечивается аутентификация. Однако такая схема не защищена от атак на основе воспроизведения сообщений.

7. Криптография с использованием эллиптических кривых

Большинство продуктов и стандартов криптографии с открытым ключом основано на алгоритме RSA. Однако в связи с развитием методов криптоанализа и вычислительной техники число битов ключа, необходимое для надежной защищенности RSA, в последние годы резко возросло, что обусловило рост загрузки систем в приложениях, использующих RSA. Это породило множество проблем, особенно для узлов связи, специализирующихся на электронной коммерции, где требуется защита больших транзакций. В связи с этим появился конкурент RSA — это криптография на основе эллиптических кривых (ЕСС — Elliptic curve cryptography). Появились стандарты по криптографии с открытым ключом ЕСС, например, IEEE P1363.

Привлекательность подхода на основе эллиптических кривых по сравнению с RSA заключается в том, что с использованием эллиптических кривых обеспечивается эквивалентная защита при меньшем числе разрядов ключа, вследствие чего уменьшается загрузка процессоров приёмопередающих устройств.

Свойства эллиптических кривых. Эллиптические кривые описы-

ваются кубическими уравнениями следующего вида:

где a, b, c, d, g являются целыми числами.

Определение эллиптической кривой включает некоторый элемент, обозначаемый О и называемый несобственным элементом (точкой бесконечности, нулевым элементом).

Из определения эллиптической кривой следует, что если три точки эллиптической кривой лежат на одной прямой линии, то их сумма есть О. Из этого определения вытекают следующие правила сложения над точками эллиптической кривой:

1)объект О выступает в роли нулевого элемента при сложении, т.е.

О= – О и для любой точки на эллиптической кривой Р + О = Р;

2)вертикальная линия пересекает эллиптическую кривую в двух точ-

ках с одной и той же абсциссой х. Эта линия пересекает кривую и

той же координатой х, но с противоположным по знаку координатой у;

52

3)чтобы сложить две точки Q и R с разными координатами х, необходимо провести через эти точки прямую и найти третью точку

пересечения Р1 этой прямой с эллиптической кривой. Существует только одна точка, если прямая не является касательной к эллиптической кривой в какой-либо из точек. В таком случае нужно по-

ложить Р1 = Q или Р1 = R, соответственно. Затем нужно воспользоваться выражением Q + R= – Р1 ;

4)чтобы удвоить точку Q, необходимо провести касательную в точке

Q и найти другую точку пересечения S. Тогда Q + Q = 2Q = – S. Вышеприведенные свойства сложения подчиняются всем обычным свойствам сложения, например, коммутативному и ассоциативному законам. Умножение точки Р эллиптической кривой на положительное число k также определено: это сумма k копий точки Р. Так, 2Р = Р + Р, 3Р = Р +

+Р + Р и т. д. Следовательно, в случае криптографии с использованием эллиптических кривых приходится иметь дело с редуцированной формой эллиптической кривой, которая определяется над конечным полем.

Особый интерес для криптографии представляет объект, называемый эллиптической группой по модулю р, где р является простым числом. Такая группа определяется следующим образом. Выберем два неотрицательных целых числа а и b, которые меньше р и удовлетворяют условию (детерминанту)

4а3 + 27b2 mod p ≠ 0,

тогда Ер(а,b) обозначает эллиптическую группу по модулю р, элемента-

ми которой являются пары неотрицательных целых чисел (х, у), которые меньше р и вместе с точкой в бесконечности О удовлетворяют условию

у2 ≡ (х3 +ах+b)(mod p).

Эллиптическая кривая над полем действительных чисел с ненулевым дискриминантом представляет собой гладкую кривую, в каждой точке которой можно провести касательную. В случае характеристики 2 существуют две разновидности эллиптических кривых: суперсингулярные и несуперсингулярные. Суперсингулярные — это эллиптические кривые, для ко-

торых левая часть уравнения (7.1) имеет вид у2 +by . Несуперсингулярные — это эллиптические кривые, для которых левая часть уравнения (7.1) имеет вид у2 + аху. Эллиптической кривой соответствует эллиптический интеграл, не берущийся в элементарных функциях.

Для модуля р=23 рассмотрим эллиптическую кривую у2 ≡ х3 + х+1. Детерминант (4 13 +27 12 ) mod 23 =8 ≠ 0 , что удовлетворяет условиям эллиптической группой по модулю 23.

53

Для эллиптической группы рассматриваются только целые значения от (0, 0) до (р, р) в квадранте неотрицательных чисел, удовлетворяющих уравнению по модулю р.

Нахождение точек на эллиптической кривой производится по следующему алгоритму:

1) для каждого значения х, удовлетворяющего 0 ≤ x < p, вычисляется

(х3 +ах+b) mod p ;

2)для каждого из полученных на предыдущем шаге значений выясняется, имеет ли это значение корень квадратный по модулю р. Если нет, то во множестве Ер(а,b) нет точек с этим значением х. Если корень существует, то имеются два значения у, соответствующих операции извлечения квадратного корня (исключение составляет случай у = 0). Эти значения (х, у) и будут точками

Ер(а,b).

Правила сложения вЕр(а,b) соответствуют геометрическим приемам, которые могут быть записаны следующим образом :

1)Р+О = Р;

2)если Р = (х, у) , то Р + (х, − у) = О. Точка (х, − у) является отрица-

тельным значением точки Р и обозначается (–Р). Точка (х,−у) лежит на эллиптической кривой и принадлежит Ер(а,b);

3)если Р = (х1, у1) и Q = (х2 , у2 ), где Р ≠ Q , то Р+Q = (х3, у3) определяется в соответствии с правилами

Для примера рассмотрим следующий случай. Пусть Р = (0,0) на эл-

липтической кривой

у2 + у = х3 − х2 .

Требуется найти 2Р = Р + Р , 3Р= Р + Р + Р.

54

Решение. Преобразуем уравнение эллиптической кривой путем замены переменных у = у′−1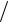2 и х = х′+1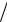3 к виду

у′2 = х′3 − х′ 3 + (1 4 − 2 27).

На этой кривой точка Рстановится точкой Q = (–1/3, ½). Используя формулы удвоения, получим 2Q = (2 / 3, –½). Далее вычисляем 3Q = (2 / 3, ½). Заметим, что 3Q = –(2Q), и следовательно, Q является точкой порядка 5, т.е. 5Q = О. Возвращаясь к исходной кривой, имеем 2Р = (1,−1) ,

3Р = (1,0) = −2Р.

Не трудно показать, что операция сложения точек эллиптической кривой коммутативна и ассоциативна, т.е. множество точек вместе с точ-

кой бесконечности О образует абелеву группу. Такое доказательство получают в проективной геометрии с использованием следующего утверждения:

если три прямые L1, L2 , L3 пересекают кубическую кривую в девяти точках Р1, Р2 ,..., Р9 с возможностью совпадения и пусть L1′, L2′, L3′ — три прямые, пересекающие эллиптическую кривую в точках Q1,Q2,...,Q9 , при

этом Рi = Qi , i =1,8 , то такжеР9 = Q9 .

Более естественно точка бесконечности определяется в проективных координатах.

Проективной плоскостью над полем F называется множество классов эквивалентности троек (X ,Y , Z ) , в которых хотя бы один элемент ненулевой. Эквивалентными считаются тройки, если элементы одной из них получаются умножением на скаляр другой: (X ′,Y′, Z′) (X ,Y , Z ) , если для некоторого элемента λ F (λX ′,λY′,λZ′) = (X ,Y , Z ) , такие классы эквивалентности называются проективными точками. Проективные точки с ненулевым элементом Z принадлежат классу эквивалентности, содержа-

определена как множество всех точек (х, у) обычной (аффинной) плоско-

сти с дополнением точек, для которых Z = 0. Эти точки можно представить как линию в бесконечности и рассматривать эту линию как «горизонт» плоскости. Всякое уравнение G(X ,Y ) = 0 кривой в аффинной плос-

Например, если применить эту процедуру к аффинному уравнению эллип-

55

тической кривой у2 = х3 + ах+b , то получится проективное уравнение

Y 2Z = X 3 + аXZ 2 +bZ 3 . Это уравнение выполняется для проективной тройки (X ,Y , Z ) , Z ≠ 0 тогда и только тогда, когда соответствующая аф-

финная точка (х, у), где х = X / Z , у =Y / Z удовлетворяет уравнению

эллиптической кривой у2 = х3 + ах+b .

Какие еще проективные точки (X ,Y , Z ) , кроме точек с Z ≠ 0 , удов-

летворяют уравнению ~ = ? Подставляя в уравнение, по-

G(X ,Y , Z ) 0 Z = 0

лучаем Х3 = 0. Но имеется только один класс эквивалентности троек (X ,Y , Z ) , где оба элемента Х и Z ненулевые — класс, содержащий (0, 1, 0).

Это и есть точка, которую обозначаем О. Это точка пересечения оси у с линией бесконечности.

Для эллиптической кривой характеристики 2 используются следующее представление:

1) для несуперсингулярного случая используется представление у2 + а1ху = х3 + а2х2 + а6 и формулы при сложении различных точек выглядят так

56

а при удвоении

Определим свойства эллиптических кривых над полем Галуа GF(2n ) . Рассмотрим также суперсингулярные и несуперсингулярные эл-

липтические кривые, основное различие между которыми состоит в том, что для суперсингулярных кривых известен порядок (количество точек)

соответствующей группы (в данном случае GF(2n ) ).

При нечетном n имеется 3 класса изоморфных суперсингулярных эллиптических кривых (при четном n имеется 7 классов), стандартными представлениями которых являются кривые:

ε1 : у2 + у = х3,

ε2 : у2 + у = х3 + х,

ε3 : у2 + у = х3 + х+1.

При нечетном n число точек первой кривой равно 2n +1 и

2n ± 2n+1 +1 для второй и третьей (знак + или – выбирается в зависимости от кривой и от сравнения по модулю 8). Группы этих кривых при не-

четном n являются циклическими. Указанные значения легко вычисляются с использованием теоремы Вейля.

Теорема Вейля. Пусть ε — эллиптическая кривая над полем Fq и m –– порядок ее группы. Тогда для порядка M (n) группы эллиптической кривой εFqn над любым полем Fqn , являющимся расширением поля Fq , справед-

лива формула

M (n) = qn −αn − βn +1,

где α и β — корни квадратного уравнения х2 −tx + q = 0, в котором коэффициент t = q + m +1.

По теореме Хассе [10] выполняется неравенство t2 ≤ 4q и в случае строгого неравенства корни квадратного уравнения α и β будут ком-

плексными.

В качестве примера найдем порядок группы эллиптической кривой в случае ε2 . Рассматривая ε2 над полем GF(2), получим на ней точки: (0,0), (0,1), (1,0), (1,1) и нулевой элемент О — всего пять элементов цикли-

57

ческой группы. Таким образом, q = 2, m = 5, t = – 2, откуда находим кор-

Окончательно получаем

М(n) = 2n +1+ 2n+1 , если n ≡ ±1(mod8) ,

М(n) = 2n +1− 2n+1 , если n ≡ ±3(mod8).

Для определения порядка группы эллиптической кривой существуют другие методы : см. алгоритм Скуфа и др.

Определив порядок группы эллиптической кривой, мы должны еще убедиться, что в его реальном разложении на простые множители содержатся большие простые числа, чтобы избежать простых случаев вычисления дискретного логарифма.

Операция сложения на основе эллиптических кривых является аналогом операции умножения по модулю простого числа в RSA, а многократное повторное сложение — аналогом возведения в степень. Криптографическую систему на основе эллиптических кривых строят на основе трудности решения проблемы разложения на множители произведения двух простых чисел. В одних случаях, например, для аддитивной группы, заданной на множестве вычетов целых чисел по модулю простого числа эта проблема легко решается с использованием процедуры на основе алгоритма Евклида. В других случаях, например, для мультипликативной группы на множестве классов вычетов положительных чисел по модулю

58

простого числа субполиномиальные алгоритмы для этой проблемы неизвестны. Для группы точек эллиптической кривой трудность проблемы дискретного логарифма не уступает сложности этой проблемы в общей постановке для произвольной группы. Исключение составляют некоторые суперсингулярные эллиптические кривые, для которых проблема дискретного логарифма решается эффективно.

7.1. Аналог обмена ключами по схеме Диффи-Хеллмана

Обмен ключами с использованием эллиптических кривых может быть выполнен следующим образом. Сначала выбирается большое простое число p и параметры а и b для эллиптической кривой в уравнении (7.1).

Это задает эллиптическую группу точек Ер(a,b). Затем в Ер(a,b) выби-

рается генерирующая точка G = (х, у). При выборе G важно, чтобы наименьшее значение n, при котором nG = O оказалось очень большим простым числом. Параметры Ер(a,b) и G криптосистемы являются парамет-

рами, известными всем участникам.

Обмен ключами между пользователями А и В можно провести по следующей схеме:

1)сторона А выбирает целое число nА < n . Это число будет личным ключом участника А. Затем участник А генерирует открытый ключ РА = nА ×G . Открытый ключ представляет собой некоторую точку из Ер(a,b);

2)сторона В выбирает аналогично личный ключ nВ и вычисляет открытый ключ РВ = nВ ×G ;

3)участник А генерирует секретный ключ К = nА × РВ, а участник

В генерирует секретный ключ К = nВ × РА.

Две формулы, полученные в п. 3) дают один и тот же результат, поскольку

nА × РВ = nА ×(nВ ×G) = nВ ×(nА ×G) = nВ × РА.

Чтобы взломать эту схему, нарушитель должен будет вычислить k по данным G и kG , что представляется трудным делом.

В качестве примера выберем р = 211, Е211(0, – 4) , что соответствует эллиптической кривой у2 = х3 − 4 и G = (2,2). Нетрудно сосчитать, что 241G = О. Личным ключом участника А является nА =121, поэтому открытым ключом участника А будет РА =121(2,2) = (115,48) . Личным ключом участника В будет nВ = 203, поэтому открытым ключом участ-

59

ника В будет РВ = 203(2,2) = (130,203) . Общим секретным ключом яв-

ляется 121(130, 203) = 203 (115, 48) = (161, 169).

В случае криптографии на основе эллиптических кривых секретный ключ представляет собой пару чисел. Если этот ключ предполагается использовать для традиционного шифрования, то из этой пары чисел необходимо сгенерировать одно подходящее значение. Можно, например, ис-

пользовать одну из координат: х или у.

7.2. Протокол обмена ключами по схеме Месси-Омуры

Пусть Е — эллиптическая кривая порядка n, а е — некоторое целое , причем, (е, n) =1, 1 < e < n . Используя алгоритм инвертирования, найдем

Используем то свойство, что законы модулярной арифметики над целыми числами и над точками эллиптической кривой идентичны. Любую

точку Р эллиптической кривой можно вычислить по формулам

Q = eP ,

R = dQ .

Очевидно, что Q = P . Протокол Месси-Омуры основан на этой идее,

реализуемой с учетом трудности решения проблемы определения скалярного множителя, соответствующего данной точке эллиптической кривой относительно базовой точки, умножаемой на этот скаляр, т.е. на проблеме дискретного логарифма для эллиптических кривых.

Обмен ключами между пользователями А и В можно провести по следующей схеме:

1) сторона А выбирает целое число еА < n и вычисляет по формуле (7.2) dА. Это число еА будет личным ключом шифрования участника А. Число dА будет личным ключом расшифрования участника А. Затем участник А помещает свое сообщение m в некоторую точку Рm эллиптической кривой и умножая на свое секретное значение еА получает точку (генерирует открытый ключ)

РА =еАРm ;

2) сторона В выбирает аналогично еВ и dВ , которые являются личными ключами шифрования и расшифрования, соответственно, участника В. Затем участник В, умножая свое секретное значение еВ на открытый ключ РА получает точку (генерирует открытый ключ)

РВ = еВРА;

60