вопро4

Два равных вектора, моменты которых относительно любой точки пространства равны, называются эквивалентными. Векторы, которые определяются с точностью до эквивалентности, то есть, которые можно перемещать вдоль линии их действия, называются скользящими.

Примером скользящего вектора может служить вектор, изображающий угловую скорость твердого тела или вектор, изображающий силу, приложенную к твердому телу.

Если вектор можно переносить в пространстве параллельно самому себе, то такой вектор называется свободным. Под словами "можно переносить" понимается, что указанные действия не нарушают условий задачи или не изменяют рассматриваемого явления и его характеристик. Примером свободного вектора может служить скорость точек твердого тела при поступательном его движении.

Вопрос о том, какие векторы являются свободными, скользящими или приложенными, в математике определяются условием задачи, а в приложениях - сущностью явления.

Две системы векторов считаются эквивалентными, если они вызывают одинаковое состояние некоторого объекта или одинаково характеризуют данное явление. Термины "одинаковое состояние", "одинаково характеризуют" не являются математически точными. Поэтому для системы скользящих векторов вводятся некоторые аксиомы.

1.Совокупность двух скользящих векторов эквивалентна нулю (нуль вектору) тогда и только тогда, когда они равны по величине, действуют по одной прямой, проходящей через произвольные токи их приложения, и направлены в противоположные стороны.

2.Если к данной системе векторов присоединить или отбросить систему, эквивалентную нулю, то в результате получится новая система, эквивалентная данной.

3.Любой вектор эквивалентен двум векторам, имеющим то же начало, для которых он равен сумме. Два вектора, имеющие общее начало, эквивалентны одному вектору, приложенному к той же точке и равному их сумме.

Теорема. Система свободных векторов эквивалентна равнодействующему вектору, равному главному вектору системы.

Например, при поступательном движении твердого тела все его точки имеют одинаковую скорость, т.е. скорость в поступательном движении есть свободный

Теорема. С помощью элементарных операций (перенос вектора вдоль линии его действия - добавление или отбрасывание двух векторов, эквивалентных нуль вектору, замена нескольких векторов, приложенных в одной точке, их суммой, замена одного вектора его составляющими) любую систему скользящих векторов всегда можно привести к двум векторам.

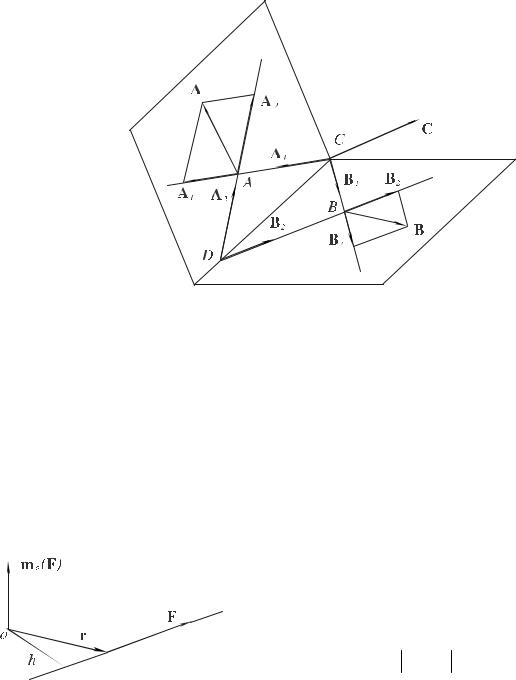
Для доказательства этого утверждения преобразуют три произвольных вектора к двум векторам. Через точку приложения C вектора C и векторы A и B проводятся соответственно две плоскости. На линии пересечения этих

сдвигаются по линии их действия в точки C и D . Итак, в точке D имеем два вектора A2 , B2 и в точке C - три вектора A1 , B1 ,C, которые заменяются соответственно суммами A2 +B2 , A1 +B1 +C.

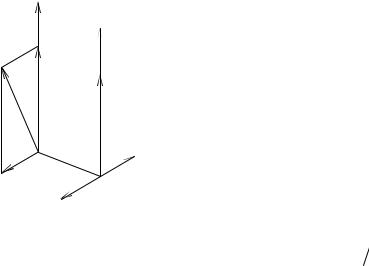
Напомним определение момента.

Моментом mo (F) вектора F относительно

какой-либо точки o называется вектор, равный векторному произведению радиусвектора r , проведенного из точки o в точку

приложения вектора на сам вектор F

mo (F)= r ×F, mo (F) = hF ,

где h -плечо вектора F .

Момент вектора не зависит от выбора точки приложения вектора на линии его действия, то есть точку на этой прямой можно брать произвольно

yFZ − zFY = M X , zFX − xFZ = M Y , xFY − yFX = M Z .

Эта система уравнений определяет прямую, то есть вектор F и его момент относительно некоторой точки mo (F) однозначно определяют линию действия

вектора.

Два равных вектора, моменты которых относительно любой точки пространства равны, называются эквивалентными. Векторы, определенные с точностью до эквивалентности, называются скользящими.

Вводятся понятия главного вектора и главного момента системы векторов:

R = ∑in=1 Fi , (3.4.1)

Главный момент системы векторов относительно нового полюса o равен сумме главного момента относительно старого полюса a и момента главного вектора системы относительно нового полюса o в предположении, что главный вектор R приложен в старом полюсе a .

Отсюда получаем ряд свойств системы скользящих векторов. Главный момент системы векторов одинаков для всех точек прямой, параллельной главному вектору. Если главный вектор системы равен нулю, то главный момент не зависит от выбора полюса Mo = Ma . Скалярное произведение главного момента

системы векторов на главный вектор той же системы не зависит от выбора

Проекции главного момента системы векторов относительно разных полюсов на

Инвариантами системы векторов являются главный вектор и скалярное произведение главного вектора и главного момента R =inv, Mo R =inv .

Инвариантность здесь понимается как независимость от точки, в которой проводятся все геометрические построения, необходимые для определения главного вектора и главного момента.

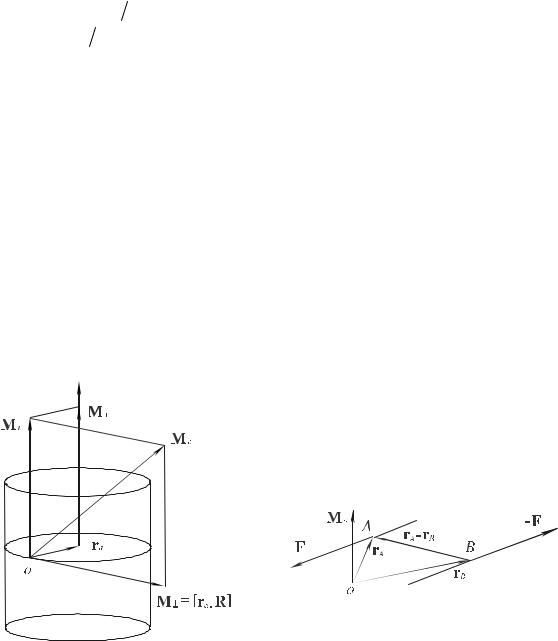
Понятие центральной оси системы векторов дает возможность представить простую геометрическую картину распределения главных моментов в пространстве. Для всех точек, лежащих на поверхности круглого цилиндра, ось которого совпадает с центральной осью системы, модули главных моментов равны между собой, или, иначе говоря, геометрическое место точек, для которых главные моменты системы векторов имеют равные модули, есть поверхность круглого цилиндра, ось которого совпадает с центральной осью системы.

R

При исследовании системы скользящих векторов встречаемся с системой двух равных по величине, параллельных и противоположно направленных скользящих векторов, которые называют парой векторов

Расстояние h между линиями действия векторов пары называются плечом пары, плоскость, проходящая через линии действия векторов пары, называется

плоскостью пары. Главный вектор пары векторов равен нулю, поэтому главный момент пары не зависит от выбора полюса, то есть одинаков для всех точек пространства. Итак, пару векторов можно переносить как угодно в плоскости ее действия; пару векторов можно переносить в любую плоскость, параллельную плоскости пары; величины векторов пары можно изменять обратно пропорционально плечу.

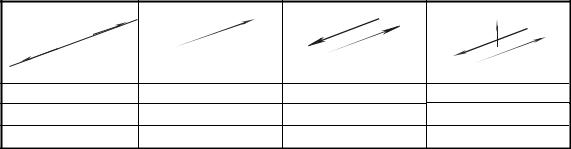
не зависит от выбора в пространстве полюса, свидетельствует о том, что момент пары есть вектор свободный. В связи с этим фактом отмечаем, что совокупность нескольких пар векторов эквивалентна одной паре, момент которой равен сумме моментов данных пар. Свойства пары векторов позволяет сформулировать теорему Л.Пуансо (1777-1859). Любую систему скользящих векторов всегда можно привести к одному скользящему вектору и одной паре, момент которой коллинеарен первому вектору.

Выше было показано, что любая система векторов может быть приведена к двум векторам. Выбирая начало системы отсчета в точке приложения одного из них, вычисляем главный вектор и главный момент, находим точку на центральной оси и проводим построения, аналогичные предыдущему. Снова получим два вектора, один из которых приложен к точке на центральной оси. Этот вектор раскладываем по двум направлениям: вдоль главного вектора и перпендикулярно главному вектору. Перпендикулярная компонента вместе с другим вектором образует искомую пару.

Простейшая совокупность векторов, к которой приводится произвольная система скользящих векторов, называется классом эквивалентности. Существует четыре класса эквивалентности: нуль вектор, вектор, пара векторов, три вектора, два из которых образуют пару, а линия действия третьего перпендикулярна плоскости пары. Критерием принадлежности к какому-либо

Теория винтов имеет непосредственное применение в кинематике. Наиболее общий случай перемещения твердого тела в пространстве сводится к винтовому перемещению, которое характеризуется осью, модулем вектора и параметром. Если винтовое перемещение бесконечно малое, то, относя его к бесконечно малому промежутку времени, получим мгновенный винт скоростей, у которого вектором служит угловая скорость, а моментом - поступательная скорость тела. Мгновенный винт скоростей также называется кинематическим винтом.

Скорость произвольной точки тела равна моменту кинематического винта относительно этой точки

определяется шестью плюккеровыми координатами, и условие линейной

ai i =1,..., n - координатами группы. За основные винты группы можно принять

какие угодно n независимых винтов, входящих в группу. Группа из шести винтов представляет такую систему, из которой линейной комбинацией с вещественными множителями можно получить любой винт. Тело, способное совершать перемещения вдоль n независимых винтов, обладает n степенями свободы. Изучение геометрического распределения всех винтов, вдоль которых

сопровождающий трехгранник совершает два движения: поступательное, со скоростью и вращательное, с

угловой скоростью Ω = e3ω. Найти ось винта.

Действительно, скалярное произведение вектора V и вектора Ω отлично от нуля .V// = V Ω Ω = h. Выбор точки приведения позволяет обратить в нуль

компоненты линейной скорости, перпендикулярные вектору угловой скорости. Центральная ось коллинеарна вектору Ω, и ее след на плоскости Oxy (точка

yo = −y, xo = −x. Таким образом, ось Oz системы отсчета является

центральной осью. Скорость произвольной точки тела, связанного с естественным трехгранником, равна моменту кинематического винта