
для решения / Тема 1-2
.pdfСодержание |
|
ТЕМА 1.2. Радиосигналы и их спектральный анализ............................................... |
1 |
Модуляция. Основные понятия................................................................................ |
1 |
Радиосигналы с амплитудной модуляцией............................................................. |
2 |
Спектральный состав радиосигнала с гармонической (тональной) AM ............. |
2 |
Радиосигналы с угловой модуляцией...................................................................... |
6 |
Внутриимпульсная модуляция................................................................................. |
9 |
ТЕМА 1.2. Радиосигналы и их спектральный анализ |
|
Модуляция. Основные понятия |
|
Радиосигнал (1.14) u(t) =U(t) cos{ω0t +ϕ0 }=U(t) cosψ(t) описывает при U(t) =
U= const, ф(0 = О простое гармоническое колебание, не содержащее информации (характерное свойство любого детерминированного сигнала, т. е. сигнала, все параметры которого известны).
Пустьs(t) — подлежащийпередачеисодержащий,«несущий»информацию (и следовательно, случайный) или информационный сигнал. Если реализуется какая-либо функциональная связь между s(t) и параметрами радиосигнала (1.14), например
U(t) = ks(t)
где k — коэффициент пропорциональности, то радиосигнал
u(t) =U(t) cos(ω0t +ϕ0 ) = ks(t) cos(ω0t +ϕ0 ) |
(2.1) |
называется модулированным радиосигналом. Он содержит информацию о сигнале s(t) и гармоническим уже не является. Сигнал (2.1) может быть сформирован устройством, структурная схема которого приведена на рис. 2.1. Устройство, осуществляющее модуляцию, называется модулятором; в рассматриваемом примере модулятор перемножает два сигнала и реализует амплитудную модуляцию (AM) несущего колебания cos{ω0t +ϕ0 }Если при U(t) =
U= const реализуется некоторая функциональная связь между s(t) и полной фазой сигнала (1.14) ψ(t) , то говорят об угловой модуляции.
Используются также и такие виды модуляции, при которых информационный сигнал s(t) функционально связан с U(t) и ψ(t) одновременно.
Необходимость применения для передачи информации модулированных радиосигналов связана с двумя основными обстоятельствами. Во-первых, при радиопередаче следует использовать сигнал, эффективно излучаемый антенной. Но эффективное излучение имеет место лишь тогда, когда геометрические размеры антенны соизмеримы с длиной волны λ = с/ f (с — скорость света)
излучаемого колебания. Это положениедиктует целесообразностьиспользования в качестве несущего колебания относительно высокочастотного гармонического сигнала.
Во-вторых, для неискаженной передачи (прохождения) радиосигнала через радиотехнические цепи и антенно-фидерное устройство необходимо, чтобы
1

эффективная ширина спектра (см. § 1.5) передаваемого радиосигнала была мала по сравнению с частотой несущего колебания, ∆ωэфГ << ω0 ; последнее условие
узкополосности радиосигнала часто записывают в форме
∆ωэфГ |
= |
∆fэфГ |
<<1 |
(2.2) |
ω0 |
|
f0 |
|
|
Радиосигналы с амплитудной модуляцией
Для выделения из принимаемого приемником высокочастотного AMколебания информационного (модулирующего) сигнала s(t), или, с точностью до постоянного множителя, ks(t), используют амплитудный детектор (детектор огибающей). Поэтому «классический» АМ-сигнал не формируют, реализуя алгоритм (2.1) непосредственно, т. е. полагая U(t) = ks(t). Если s(t) принимает отрицательные значения (рис. 2.2, а), то огибающая, выделяемая амплитудным детектором, уже не будет соответствовать s(t) (рис. 2.2, б). Модулирующий множитель представляется в виде
U(t) =U0 + ks(t) , где U0 ≥ ks(t)
и АМ-сигнал формируют как
sAM = (t)u(t) = {U0 + ks(t)}cos(ω0t +ϕ0 )
Детектор огибающей выделяет (рис. 2.2, в) сигнал U(t), соответствующий информационному с точностью до постоянной составляющей и постоянного множителя.
Спектральный состав радиосигнала с гармонической (тональной) AM
Как уже отмечалось в § 2.1, реальный информационный (модулирующий) сигнал s(t) детерминированным быть не может. Но для изучения основных особенностей модулированных сигналов в качестве s(t) используют модели детерминированных сигналов. Простейшей моделью АМ-сигнала является колебание с гармоническим модулирующим сигналом
U(t) =U0 + ∆U cos(Ωt +ϕΩ0 )
где ϕΩ0 — начальная фаза сигнала модуляции,∆U = const . В этом случае
u(t) = {U0 + ∆U cos(Ωt +ϕΩ0 )}cos(ω0t +ϕ0 ) =U0 {1 + m cos(Ωt +ϕΩ0 )}=U0 cos(ω0t +ϕ0 ) + mU2 0 cos{(ω0 + Ω)t +ϕ0 +ϕΩ0 }+ mU2 0 cos{(ω0 −Ω)t +ϕ0 −ϕΩ0 },
(2.3)
где m= ∆U /U0 — коэффициент амплитудноймодуляции, О ≤m < 1. Формула
(2.3) определяет модель и спектральный состав АМ-сигнала с гармонической модуляцией; (иногда говорят «сигнал, модулированный чистым тоном», или «сигнал с тональной модуляцией»). Принято называть (ω0 ) несущей,ω0 + Ω. —
верхней боковой, ω0 −Ω— нижней боковой частотами.
Амплитудная и фазовая спектральные характеристики радиосигнала с гармонической AM изображены на рис. 2.3, а, б; осциллограмма сигнала приведена на рис. 2.4.
2
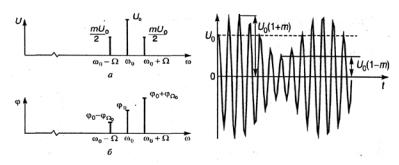
Из графика, представленного на рис. 2.4, и выражения (2.3) видно, что максимальное и минимальное значения огибающей сигнала составляют соответственно
Umax =U0 (1 + m),Umin =U0 (1 − m),
Рис. 2.3. Амплитудный (а) и фазовый (6) спектры радиосигнала с гармонической амплитудной модуляцией
Рис. 2.4. Радиосигнал с гармонической амплитудной модуляцией откуда следует формула для определения коэффициента т по
осциллограмме:
m = Umax −Umin |
(2.4) |
Umax +Umin |
|
Тональный АМ-сигнал часто используется в лабораторной практике, при настройке радиоаппаратуры и т. п.
Эффективная ширина спектра радиосигнала с тональной AM определяется очевидным соотношением
∆ωэфAM = 2Ω |
(2.5) |
Векторная диаграмма радиосигнала с тональной AM. Диаграмма поясняет процесс формирования АМ-сигнала. Построение связано с использованием хорошо известного из курса теоретической электротехники символического метода, или метода комплексных амплитуд, сущность которого состоит в представлении гармонического сигнала в виде вещественной части комплексной функции:
s(t) =U0 cos(ω0t +ϕ0 ) = Re{U0e |
j(ω t+ϕ |
) |
}= Re{U0e |
jϕ |
0 e |
jω t |
|
|
. |
|
|
|
||
0 0 |
|
|
0 |
}= Re s(t) , |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
. |
|
|
— комплексная амплитуда |
||||
где s(t) =U0e jω0t — комплексный сигнал, |
|
U 0 e jϕ0 |
||||||||||||
сигнала s(t), содержащая информацию об амплитуде U0 |
и начальной фазе ϕ0 |
|||||||||||||
сигнала s(t); ее изображают вектором на комплексной плоскости. |
|
|
|
|||||||||||
Представим таким образом радиосигнал (2.3): |
|
|
|
|
(t)e jω0t . |
|||||||||
u(t) = Re U e jϕ0 + mU0 e j(ϕ0 +ϕΩ0 )e jΩt + mU0 e jΩt |
+ mU0 e j(ϕ0 −ϕΩ0 )e− jΩt e− jω0t = Re U |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
0 |
2 |
|
|
2 |
|
|
2 |
|
|
|
|
AM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
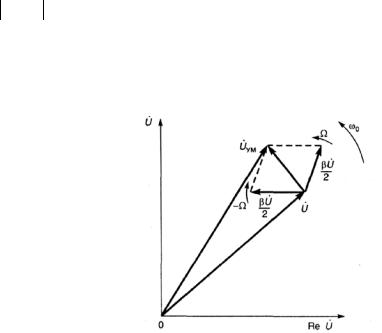
Комплексная амплитуда радиосигнала с тональной AM оказывается функцией времени; ее называют комплексной огибающей АМ-сигнала.
Векторная диаграмма показана на рис. 2.5. Вектор U AM. (0) представлен на
|
. |
1 |
. |
jϕ |
|
|
комплексной плоскости как сумма векторов |
|
|
||||
, Uб+ = 2 mU0e Ω0 |
и |
|||||
U0 =U0 |
||||||
3 |
|
|
|
|
|
|

|
1 . |
− jϕ |
|
помещенных в систему координат, вращающуюся против |
Uб− = |
2 mU0e |
|
Ω0 |
часовой стрелки с угловой скоростью (круговой частотой) ω0 . В этой системе
|
. |
неподвижен. |
|
|
|
|
|
. |
. |
|
координат вектор U 0 |
Векторы боковых составляющих Uб+ и |
Uб+ |
||||||||
всегда расположены |
симметрично |
относительно вектора |
. |
и вращаются |
||||||
U 0 |
||||||||||
соответственно с угловыми скоростями ±Ω. При этом вектор |
. |
|
||||||||
U AM (t), модуль |
||||||||||
которого изменяется по закону |
|
|
|
|
|
|
|
|||
|
U AM (t) =U0 {1 + m cos(Ωt +ϕΩ0 } |
|
|
|
|
|
|
|||
всегда |
коллинеарен |
. |
|
. |
|
|
вещественную |
ось |
||
U 0 . Проекция |
U AM (t) на |
|||||||||
|
|
|
|
. |
|
|
, совпадает с u(t). |
|
||
вращающейся системы координат, или Re U AM (t) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Радиосигнал с многотональной AM. Если в модулирующий множитель |
||||||||||
входит сумма косинусоид |
|
|
|
|
|
|
|
|
||
u(t) =U0 |
{1 + m1 cos(Ω1t +ϕΩ10 ) + m2 cos(Ω2t +ϕΩ20 ) +...}×cos(ω0t +ϕ0 ), |
|
|
|||||||
то кроме несущей частоты, в спектральном составе сигнала появится ряд боковых частот:
Рис. 2.5. Векторная диаграмма радиосигнала с гармонической амплитудной модуляцией
ω0 ± Ω1, ω0 ± Ω2 , ... Все сказанное о тональном АМ-сигнале сохраняет силу и
для АМ-сигнала с многотональной модуляцией. Легко построить и соответствующую векторную диаграмму. На парциальные коэффициенты модуляции m1, m2 ,..., mk необходимо наложить условие ∑mk ≤1. Полоса частот,
k
занимаемая спектром радиосигнала с многотональной AM, определяется соотношением
∆ωэфAM = 2Ωmax |
(2.6) |
где Ωmax — максимальная частота дискретного спектра модулирующего сигнала.
Спектр АМ-радиосигнала в общем случае. В реальной ситуации случайной модулирующей функции соответствует Фурье-преобразование, в которое могут входить как дискретные δ -составляющие, так и континуальная (сплошная) часть (смешанный спектр). Характер спектра АМ-радиосигнала в этом случае можно представить качественно, опираясь на выражение (1.43) и рис. 1.9. Разумеется, форма спектральной функции АМ-радиосигнала будет определяться видом
4
конкретного модулирующего сигнала s(t) и может радикально отличаться от спектра прямоугольного радиоимпульса, изображенного на рис. 1.9.
Полоса частот, занимаемая АМ-сигналом при произвольном законе модуляции, определяется соотношением (2.6), где Ωmax — максимальная (по некоторому избранному критерию, см. § 1.5) частота спектральной функции модулирующего сигнала.
Корреляционная функция АМ-радиосигнала. В формулу (1.71), определяющую КФ сигнала с неограниченной энергией,
|
|
|
|
|
|
1 |
|
T / 2 |
|
|
|
|
|
|
B(τ) = Tlim→∞ |
|
∫s(t)s(t −τ)dt, |
|
|
||||||
|
|
T |
|
|
|
|||||||
|
|
|
|
|
|
|
−T / 2 |
|
|
|
||
подставим выражение (2.1) для АМ-сигнала u(t) =U(t) cos(ω0t +ϕ0 ) . положим |
||||||||||||
ϕ0 и вычислим интеграл: |
|
|
|
|||||||||
|
|
|
1 |
T / 2 |
|
|
|
|
1 |
T / 2 |
||
B(τ) = lim |
∫ U(t) cosω0t U(t −τ) cosω0 (t −τ)dt = Tlim→∞ |
∫U(t)U(t −τ) cosω0τdt,+ |
||||||||||
T |
2T |
|||||||||||
|
|
|
−2 |
|
|
|
T →∞ |
−T / 2 |
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
T / 2 |
|
|
|
|
|
|
|
|||
+ lim |
∫ |
U(t)U(t |
− |
τ) cos(2ω |
t −ω τ)dt. |
|
|
|||||
|
|
|
||||||||||
T →∞ |
2T |
|
|
|
0 |
0 |
|
|
||||
|
−T / 2 |
|
|
|
|
|
|
|
||||
Можно показать, что с учетом медленного изменения огибающей АМсигнала U(t), второй интегралравен нулю как интеграл отбыстроосциллирующей функции. Вынося за знак первого интеграла cosω0τ , получаем:
|
|
|
|
|
|
|
|
T |
|
||
B(τ) = |
1 cosω0τ Tlim→∞ |
1 |
∫2 U(t)U(t −τ)dt = |
1 BU (τ) cosω0τ, (2.7) |
|||||||
T |
|||||||||||
|
|
2 |
|
|
|
|
− |
T |
2 |
||
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
T |
|
|
|
|
|
||
гдеBU (τ) = Tlim→∞ |
1 |
∫2 |
U(t)U(t −τ)dt — корреляционная функция огибающей АМ- |
||||||||
T |
|||||||||||
|
|
|
− |
T |
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
сигнала. Но |
1 cosω0τ — корреляционная функция (1.73) гармоники cosω0t ; тем |
||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
самым показано, что корреляционная функция радиосигнала с AM есть произведение КФ огибающей и КФ несущего колебания. \
Распределение мощности в спектре АМ-радиосигнала. В соответствии с представлением (2.3) и результатом (1.67), полученным в §1.9, средняя мощность радиосигнала с тональной AM определяется суммой средних мощностей его гармонических (несущей, нижней и верхней боковых) составляющих:
P = P |
+ P |
+ P |
= P |
+ P |
= U 2 |
+ m2U 2 |
+ m2U 2 |
= U 2 |
+ m2U 2 |
НЕС |
бокв |
бокн |
нес |
бок |
2 |
8 |
8 |
2 |
4 |
|
|
|
|
|
Этот простой результат показывает, что часть мощности АМ-радиосигнала (2.3), расходуемая на передачу собственно информационной составляющей спектра (КПД амплитудной модуляции), относительно невелика:
|
|
|
P |
m2 |
|
η |
AM |
= |
бок |
= |
|
|
|
P |
2 + m2 |
||
и даже при практически никогда не используемом коэффициенте модуляции m = 1 составляет около 33%. Исторически AM была первым применяемым методом модуляции, и среди многих (в том числе и более важных)
5

обстоятельств небольшое значение ηAM явилось стимулом поисков альтернативных видов модуляции.
Радиосигналы с угловой модуляцией
Положив в выражении (1.14) U(t) = U= const, получим модель радиосигнала с угловой модуляцией (УМ):
sУМ (t) = u(t) =U cos{ω0t +ϕ(t) +ϕ0 }=U cosψ(t) |
(2.8) |
В гармоническом сигнале (1.1) частота ω0 есть не что иное, как скорость
изменения полной фазы. Распространяя это определение на произвольный радиосигнал, вводят понятие мгновенной частоты как производной (скорости изменения) полной фазы:
ω(t) = |
d |
ψ(t) = ω0 + |
d |
ϕ(t). |
(2.9) |
|
|
||||
|
dt |
dt |
|
||
Тогда полную фазу как аргумент тригонометрической функции в модели |
|||||
радиосигнала (1.14) можно определить как |
(2.10) |
||||
ψ(t) = ∫ω(t)dt = ω0t +ϕ(t) +ϕ0 . |
|||||
Напомним, что полная фаза произвольного радиосигнала содержит линейную часть ω0t (линейный набег фазы за время t), фазовую функцию ϕ(t) и
ϕ0 = const , которая при ϕ (t) = 0 называется начальной фазой (см. § 1.1).
Фазовая модуляция (ФМ). Пусть, как и в § 2.1, информационный (модулирующий) сигнал есть s(t), или, с точностью до постоянного множителя, ks(t). Тогда, положив ϕ0 = 0, получим для полной фазы (2.10) выражение
ψ(t) = ω0t + ks(t) , а для сигнала с фазовой модуляцией
uФМ (t) =U cos{ω0t + ks(t)}. |
(2.11) |
Частотная модуляция (ЧМ). Пусть мгновенная частота ω(t) = ω0 + ∆ω(t) , где ∆ω(t) = ks(t); тогда при частотной модуляции полная фаза
ψ(е) = ∫ω(t)dt = ω0t + k ∫s(t)dt;
сигнал с ЧМ записывается как |
|
uЧМ (t) =U cos{ω0t + k ∫s(t)dt}. |
(2.12) |
Легко заметить, что частотная и фазовая модуляции в силу соотношений (2.9) и (2.10) тесно связаны, аименно, если модулирующая функция представлена как ks(t), то ЧМ при ∆ω(t) = ks(t) = = dϕ (t)/dt соответствует ФМ по закону
ϕ(t) = k ∫s(t)dt ; ФМ при
ϕ(t) = ks(t) соответствует ЧМ по закону ∆ω(t) = k dsdt(t) .
Гармоническая УМ. Установленная связь особенно очевидна при выборе гармонического модулирующего сигнала s(t) = cosΩt . ФМ-сигнал можно тогда записать как
uФМ (t) =U cos(ω0t + ∆ϕ cos Ωt), |
(2.13) |
где ∆ϕ — девиация фазы.
6
Для ЧМ-сигнала ψ(t) =ω0 + ∆ωcosΩt с полной фазой
ψ(t) = ω0t + k ∫s(t)dt = ω0t + |
∆ω |
sin Ωt +ϕ0 . |
|
||
|
Ω |
|
Здесь ∆ω — девиация частоты, и ЧМ-сигнал можно записать как
uЧМ (t) =U cos(ω0t + |
∆ω |
sin Ωt +ϕ0 ). |
(2.14) |
|
|||
|
Ω |
|
|
Введем индекс гармонической угловой модуляции β , под которым при
частотной модуляции будем подразумевать отношение ∆ω / Ω , а при фазовой — девиацию фазы ∆ϕ , тогда анализируемый сигнал можно представить в виде
uУМ (t) =U cos(ω0t + β sin Ωt). |
(2.15) |
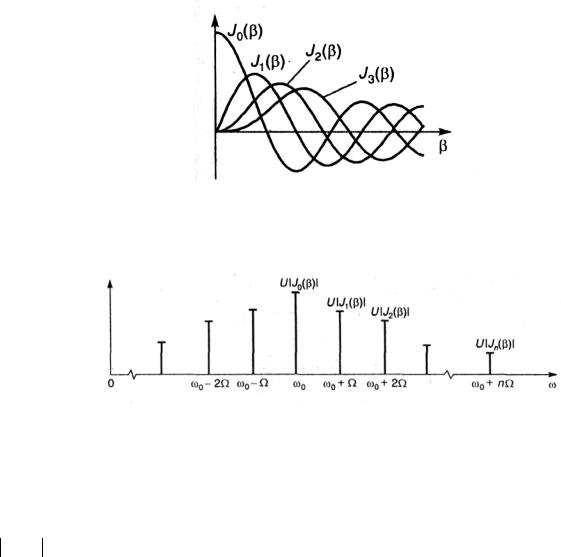
СпектральныйсоставрадиосигналапригармоническойУМ.Воспользуемся известным разложением
∞
e jβ sin x = ∑Jk (β)e jkx , k =−∞
где Jk — функцияБесселя1-го рода порядкаk отвещественного аргумента.
Замечание Функции Бесселя, являющиеся решением дифференциального уравнения
Бесселя, табулированы [12]. Примерный вид графиков первых четырех функций Jk (β) показан на рис. 2.6.
Рис. 2.6. Функции Бесселя Перепишем (2.15) в виде
|
∞ |
|
∞ |
|
uУМ (t) = Re Ue jω0t ∑Jk (β)e jk (Ωt) =U ∑Jk (β) cos[(ω0 + kΩ)t]. |
(2.16) |
|||
|
k =−∞ |
|
k =−∞ |
|
Рис. 2.7. Амплитудный спектр радиосигнала с; гармонической угловой модуляцией
На рис. 2.7 представлен амплитудный спектральный состав радиосигнала с УМ. Особенностью этой спектрограммы является бесконечное количество гармоник и необязательно монотонный характер убывания коэффициентов U Jk (β) , что связано с колебательным характером поведения функций Бесселя.
7
Структуравыражения(2.16)говоритопотенциальнобольшем,чемприAM, КПД угловой модуляции,ηУМ >ηAM . Из графиков рис. 2.6, например, видно, что
при некоторых значениях β в разложении (2.16) вообще не будет несущей компоненты на частотеω0 .
Спектральный состав радиосигнала с гармонической УМ при β « 1. При этом условии можно положить cos(β sin Ωt) ≈1, sin(β sin Ωt)β sin Ωt и представить сигнал (2.15) в виде
u(t) =U cos(β sin Ωt) cosω0t −U sin(β sin Ωt) sinω0t =U cosω0t − βU sin Ωtω0t = |
(2.17) |
||||||
U cosω0t + |
βU |
cos(ω0 |
+ Ω)t − |
βU |
cos(ω0 −Ω)t. |
||
|
|||||||
2 |
2 |
|
|||||
|
|
|
|
|
|||
Структуры амплитудных спектральных характеристик радиосигналов с гармонической угловой при β « 1 и с гармонической амплитудной модуляцией
(см.рис.2.3,а)аналогичны.Нарис.2.8приведенасоответствующаярадиосигналу с гармонической УМ при β « 1 векторная диаграмма, построенная так же, как
векторнаядиаграммарадиосигналастональнойAM(см.рис.2.5). Отрицательный
знак перед компонентой 1 βU cos(ω0 −Ω)t (180° — фазовый сдвиг) обусловливает |
||
2 |
|
|
. |
. |
что |
изменение направления вектора UУМ |
относительно вектора U во времени, |
|
характерно для угловой модуляции. |
Заметим, что в соответствии с рис. |
2.8 |
меняется во времени и модуль вектора UУМ. , хотя амплитуда радиосигнала с УМ
должна быть постоянной. Это следствие довольно грубого приближения, на основании которого записано выражение (2.17). Впрочем, с учетом условия β «
1, эти изменения, как и изменения направления UУМ. , весьма малы.
Эффективнаяширина спектра сигнала с гармоническойУМ. При k > β
величина Jk (β) быстро убывает. Поэтому в разложении (2.16) принимают в
расчет все гармоники с номерами k ≤ β + 1, а остальными пренебрегают. Тогда
полоса частот, занимаемая спектром сигнала с гармонической угловой модуляцией, определяется как
∆ωЭФУМ = 2Ω(β +1) |
(2.18) |
Рис. 2.8. Векторная диаграмма радиосигнала с гармонической УМ при малом индексе модуляции
При β » 1 эффективная ширина спектра сигнала с гармонической УМ равняется удвоенной девиации частоты:
8

∆ωЭФУМ ≈ 2βΩ = 2 ∆Ωω Ω = 2∆ω.
При β « 1 эффективная ширина спектра сигнала с гармонической УМ равняется удвоенной частоте модуляции:
∆ωЭФУМ ≈ 2Ω.
Внутриимпульсная модуляция
Для многих радиотехнических приложений большой интерес представляют импульсные радиосигналы, частота (а следовательно, I и фаза) заполнения которых изменяется по некоторому закону.
Рассмотрим радиоимпульс с линейной частотной модуляцией (ЛЧМсигнал); частота заполнения радиоимпульса с длительностью Т и прямоугольной огибающей (1.4) меняется по закону
v ю(/) = щ+yt; | 11 < Т/1. Полная фаза в соответствии с выражением
: (2.10) есть (при фо = 0)
так что ЛЧМ-сигнал представляется выражением
Примерный график ЛЧМ-сигнала, законы изменения частоты и фазы показаны на рис. 2.11.
Особенностью ЛЧМ-сигнала является, в частности, возможность управлять его базой ГД/Эф (введенным в § 1.5 параметром), при постоянной длительности импульса регулируя девиацию частоты. При значениях базы спектр ЛЧМрадиоимпульса хорошо аппроксимируется [3] финитной функцией частоты с прямоугольной огибающей:
Аюэф радиоимпульса при этом значении базы совпадает с девиацией частоты у Т.
9

Рис. 2.11. Сигнал с линейной частотной модуляцией
В силу этого свойства сигнал с ЛЧМ играет особую роль е радиоизмерительной технике: он используется в таких важных приборах, как измерители АЧХ (амплитудно-частотных характеристик) и анализаторы спектра.
Корреляционная функция ЛЧМ-сигнала. Энергетический спектр сигнала (2.24) определяется как
обратимся к соотношению (1.78) и вычислим корреляционную функцию ЛЧМ-сигнала,
Читателю рекомендуется самостоятельно обосновать выбор пределов интегрирования в (2.25). Из этого выражения следует важный вывод: ширина главного лепестка КФ обратно пропорциональна девиации частоты сигнала. Следовательно, при заданной девиации можно, увеличивая длительность (а, следовательно, и энергию) сигнала (2.24), получить узкий главный лепесток КФ с большим значением 5(0) = Е. В этом случае говорят о хороших корреляционных свойствах ЛЧМ-сигнала. Такими свойствами обладают также некоторые радиоимпульсные сигналы с ФМн (речь о них пойдет в § 5.3, посвященном применению согласованных фильтров сигналов).
Сигналы этого типа были предложены и изучались в основном для использованиявсферерадиолокационныхприложений,новнастоящеевремяони при решении задачи повышения помехоустойчивости радиоканалов находят все более широкое применение в телекоммуникационных системах.
10
