
10511
.pdf60
7.3.УСЛОВИЯ УРАВНОВЕШЕННОСТИ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
Сформулируем теперь условия, при которых произвольная пространственная система сил будет уравновешенной.
Система сил в общем случае заменяется одной силой и одной парой, но сила и пара не могут уравновесить друг друга.
Следовательно, для уравновешенности системы сил требуется, чтобы и сила, и момент пары были нулевыми.
Отсюда получаются приведенные ниже в трех формах условия уравновешенности произвольной пространственной системы сил.
Для того чтобы произвольная пространственная система сил была уравновешенной, необходимо и достаточно, чтобы выполнялись следующие условия:
1.В векторной форме:
главный вектор системы сил и главный момент системы сил относительно некоторой точки должны быть равны нулю:
|
|
|
|
|
|
|
∑ |
|
|
|
|
{ |
|
= 0 |
или |
{ |
|
|
= 0 |
(7.3) |
|||
|
|
|
|
=1 |
|
|
|||||
|
|
= 0, |
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
( ) = 0, |
|
||
|
|
|
|
|
|
|
|
|
|||
2.В геометрической форме:
многоугольники сил и моментов должны быть замкнуты.
3.В аналитической форме:
суммы проекций сил на каждую из координатных осей и суммы моментов сил относительно каждой из координатных осей должны быть равны нулю:
|
|
|
|
|
|
|
|
∑ |
|
= 0 |
|
|||
|
|
= 0 |
|
|
|
|
|
=1 |
|
|
|
|
||
|
|
|
|
|
|
|
∑ |
|
= 0 |
|
||||
|
|
= 0 |
|
|
|
|
|
|||||||
|
{ |
|
|
|
|
=1 |
|
|
|
|
||||
|
|
= 0 |
|
|
|
|
∑ |
|
|
= 0 |
|
|||
|
|
|
или |
{ |
=1 |
(7.4) |
||||||||
|
|
= 0 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
∑ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
( ) = 0 |
|
||||
|
{ = 0 |
|
|
|
=1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
{∑ |
|
|
|
|
|
||||
|
|
= 0, |
|
=1 |
|
( ) = 0 |
|
|||||||
{ |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
∑ |
|
|
|
|
|||||
|
|
|
|
{ |
=1 |
|
( ) = 0, |
|
||||||
|
|
|
|
|
|
|
|
|
||||||
Таким образом, в статике для произвольной пространственной системы сил в общем случае можно составить шесть уравнений равновесия.
61
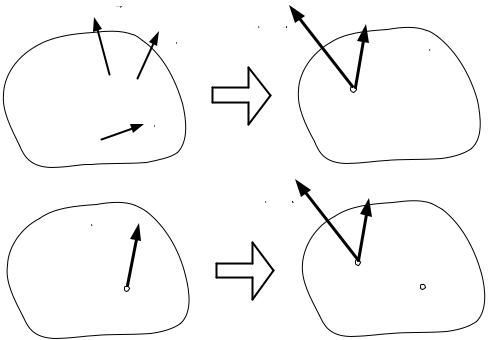
7.4. ТЕОРЕМА ВАРИНЬОНА
ТЕОРЕМА
Если система сил имеет равнодействующую, то ее момент относительно любой точки или оси равен сумме моментов всех сил системы относительно той же точки или оси.
ДОКАЗАТЕЛЬСТВО
|
|
|
|
|
|
|
(система I) имеет |
||
Пусть некоторая система сил ( |
, , … , |
|
) |
||||||
|
|
|
1 |
2 |
|
|
|
|
|
|
(рис. 7.4), приложенную в точке О (система II). |
||||||||
равнодействующую |
|||||||||
Очевидно, что системы I и II эквивалентны: |
|
|
|
|
|
||||
|
≡ ( |
, , … , |
). |
||||||
|
|
|
|
|
|
|
1 |
2 |
|
Рассмотрим любую точку пространства — точку А. |
|
||||||||
Система I |
F1 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
F2 |
M A Fi |
|
|
|
n |
|
|
|
|
i 1 |
|
|
|
* |
|
||
|
|
|
|
|
|
R Fi |
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
A |
|
|
|
|
Fn |
|
|
|
|
|
|
|
Система II |
|
|
|
|
|
|
|
|
|
|
|
|
|
M A R |
|
R* |
|
||
|
* |
|
|
|
|
|
|
|
|
R R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
O |
|
|
|
|
|
|
O |
Рис. 7.4
I. |
приведем исходную систему сил |
|
|
|
к точке А. |
( |
, , … , |
) |
|||
|
|
1 |
2 |
|
|
Система приводится к одной силе, равной главному вектору, и паре с моментом, равным главному моменту системы сил относительно точки А:
∑=1 ( )

62
II.приведем силу к точке А.
Система приводится к одной силе, равной главному вектору, и паре с моментом равным моменту равнодействующей относительно центра приведения:
().
Сравнивая результаты приведения систем I и II, мы видим, что силы в них одинаковы и приложены в одной и той же точке A.
Поскольку после приведения к центру А эти системы сил останутся эквивалентными, моменты пар также должны быть одинаковы, то есть
|
|
|
|
|
(7.5) |
|
() = ∑ |
=1 |
|
( ) |
|
|
|
|
|
|
Это и есть математическая запись теоремы Вариньона.
Проецируя равенство (7.5) на оси координат, проходящие через точку А, мы получим выражение теоремы Вариньона для моментов сил относительно осей:
|
|
|
|
|
|
() = ∑ |
=1 |
( ) = 0 |
|
||
|
|
|
|
|
|
{ |
|
|
|
|
(7.6) |
() = ∑ |
=1 |
( ) = 0 |
|||
|
|
|
|
|
() = ∑=1 ( ) = 0,
Эта теорема часто используется на практике для вычисления момента некоторой силы в том случае, когда сложно найти плечо самой силы, но легко определить плечи ее составляющих.
7.5ИНВАРИАНТЫ СИСТЕМЫ СИЛ
Первым (векторным) инвариантом системы сил является главный вектор, поскольку он не зависит от точки приведения.
В отличие от главного вектора главный момент не является инвариантом. При переносе центра приведения из точки О в точку А его величина меняется по закону
|
|
+ |
|
|
, |
|
= |
× |
|
||
|
|
|
|
|
|
где r0 − радиус-вектор, проведенный от нового центра В к точке А. Можно доказать, что при перемене центра не изменяется скалярное
произведение главного момента и главного вектора.
Действительно, умножив скалярно все слагаемые на главный вектор, получим:
∙ = ∙ + ( × ) ∙

63
Второе слагаемое в правой части равно нулю, поскольку является скалярным произведением взаимно перпендикулярных векторов.
Следовательно |
|
|
|
|
|
, что и требовалось доказать. |
|
∙ |
= |
∙ |
|
||
|
|
|
|
|
|
|
Таким образом, |
|
|
|
|
|
|
скалярное произведение главного момента на главный вектор является вторым (скалярным) инвариантом системы сил.
Итак, каждая система сил имеет две не зависящие от центра приведения характеристики:
1.векторный инвариант, которым является главный вектор R ;
2.скалярный инвариант, которым является скалярное произведение главного момента на главный вектор.
Первый и второй инварианты независимы, то есть из одного из них не следует другой.
Иногда в качестве скалярного инварианта системы сил принимают
проекцию главного момента на направление главного вектора.
Модуль главного вектора не зависит от точки приведения. Поделив на него левую и правую части равенства получим:
|
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
∙ |
|
|
|
|
|
|
|
|
||||
|
|
|
= |
|
|
|||
|
|
|
|
|
|
|||
или |
|
∙ |
|
∙ |
|
|||
|
= |
|
||||||
|
|
|
|
|
|
|
||
или |
|
∙ = |
∙ . |
|||||
|
|
|
|
|
|
|
|
|
где и углы между направлениями главного момента и главного вектора соответственно в точках A и B , а вектор представляет собой единичный направляющий вектор главного вектора.
Выражения в левой и правой частях представляют собой проекции главного момента на направление главного вектора. На рис. 7.5 показано, что для различных точек пространства эта величина одинакова, то есть не зависит от выбора центра приведения.

64
R*
а
eR
eM |
A |
R*
 MAA*
MAA*
eR
B
|
* |
|
R |
б |
в |
B |
MO |
MB |
O |
* |
* |
|
0 |
|
e |
eR |
eM |
M |
|
|
|
O |
|
Рис. 7.5
7.6. ДИНАМИЧЕСКИЙ ВИНТ, ГЛАВНАЯ ОСЬ СИСТЕМЫ СИЛ
По основной теореме статики (§7.2) система сил при приведении к произвольной точке пространства заменяется силой, равной главному вектору, и парой сил с моментом, равным главному вектору системы относительно точки приведения. Для некоторых точек пространства полученные в результате приведения главный вектор и главный момент окажутся коллинеарными, как это показано на рис. 7.5,в. Можно показать, что такие точки будут лежать на одной прямой.
Дадим определение:
геометрическое место точек, для которых главный вектор и главный момент системы сил коллинеарны, называется главной осью системы сил.
Рассмотрим случай, когда к материальному телу приложена сила и пара сил таким образом, что линия действия силы расположена перпендикулярно плоскости действия сил пары.
а |
|
|
F |
P, P |
|
б |
|
|
F |
||
|
|
|
|||||||||
|
|
m |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
P |
|
|
|
|
P |
|
P |
|
|
|
P |
|
|
|
|
|
|
|
|
||||
cos 1 |
|
|
|
|
|
|
cos 1 |
|
|
m P, P |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
(проекция положительна) |
|
(проекция отрицательна) |
|||||||||
Рис. 7.6
Эта система сил не может быть более упрощена.
Такая система сил называется динамическим винтом, силовым винтом или динамой .

65
Тема 8.
ЧАСТНЫЕ СЛУЧАИ СИСТЕМ СИЛ
В частных случаях, когда на систему сил наложены какие-либо ограничения, число необходимых уравнений равновесия может быть меньше шести, поскольку часть из них будут являться тождествами.
Рассмотрим примеры.
Наиболее важной с точки зрения практического применения является случай, когда все силы расположены в одной плоскости. Такие системы называют плоскими системами сил.
8.1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
Рассмотрим случай приведения к заданному центру O сил, произвольно расположенных на плоскости.
Пусть к твердому телу приложены силы (1, 2, … , ), лежащие в одной плоскости и приложенные соответственно в точках A1, A2 ,...., An (рис. 8.1,а).
Примем за центр приведения некоторую точку O , лежащую в этой плоскости, и приведем все силы к этому центру. В результате приведения
|
|
|
|
|
|
|
, … , |
|
|
|
|
|
|
|
|
получим систему сходящихся сил ( ′ |
, ′ |
2 |
′ ), приложенных в центре O |
||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
и |
|
лежащих в одной плоскости, а |
также |
систему присоединенных |
пар, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 8.1,б). |
||
алгебраические моменты которых равны = ( |
, ′ ) = ± |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сложив сходящиеся силы, получим главный вектор системы сил |
|
= |
||||||||||
|
|
|
|
||||||||||||
∑ |
|
|
|
, который будет лежать в той же плоскости, что и вся система. |
|
|
|||||||||
=1 |
′ |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

66
а
O
An hn
Fn
h1
....
F1  б
б
A1 F2
F2
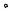 A2
A2
F1
2 |
MO F2 |
MO F1 |
|
||
|
|
|
|
|
O |
2 |
|
h2
MO Fn |
Fn |
|
в
MOO*
O
R*
Рис. 8.1
Моменты присоединенных пар равны моментам сил системы относительно центра приведения, то есть
( , ′ ) = ( ) = ±
Сложив алгебраические моменты всех сил относительно точки О, получим главный алгебраический момент системы сил относительно О^
∑ |
|
|
|
|
|
|
|
|
|
=1 |
( |
, ′ ) = ∑ |
=1 |
( ) = |
|
||||
|
|
|
|
|
|
|
|||
Таким образом (рис. 8.1,в),
силы, произвольно расположенные на плоскости, можно привести к одной силе, приложенной в центре приведения, равной главному вектору данной системы сил, и к лежащей в той же плоскости паре сил с алгебраическим моментом, равным главному алгебраическому моменту системы сил относительно центра приведения.
То есть
67
(1, 2, … , ) ≡ ( , ).
Выбор центра приведения не отражается на модуле и направлении главного вектора, но влияет на величину и знак главного момента.
8.2. УПРОЩЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ
Итак, любая плоская система сил может быть заменена
одной силой (равной главному вектору системы сил и приложенной в центре приведения О) и/или
одной парой (с алгебраическим моментом, равным главному алгебраическому моменту системы сил относительно центра
приведения ).
Однако в ряде случаев и эту систему сил можно упростить. Рассмотрим эти случаи.
1. |
Если = 0 |
и |
= 0, то система сил уравновешена (эквивалентна |
|
|
|
|
нулю), дальнейшее упрощение ее невозможно. |
|||
2. |
Если = 0 |
и |
≠ 0,то система сил эквивалентна одной паре сил, |
|
|
|
|
дальнейшее упрощение ее невозможно. |
|||
3. |
Если ≠ 0 |
и |
= 0, то система сил эквивалентна одной силе, то есть |
|
|
|
|
имеет равнодействующую, которая проходит через центр приведения О, |
|||
Дальнейшее упрощение системы невозможно. |
|||
4. |
Если ≠ 0 |
и |
≠ 0, (имеются и сила и пара), то система сил |
|
|
|
|
оказывается эквивалентной одной силе , т. е. имеет равнодействующую равную главному вектору, которая не проходит через центр приведения О.
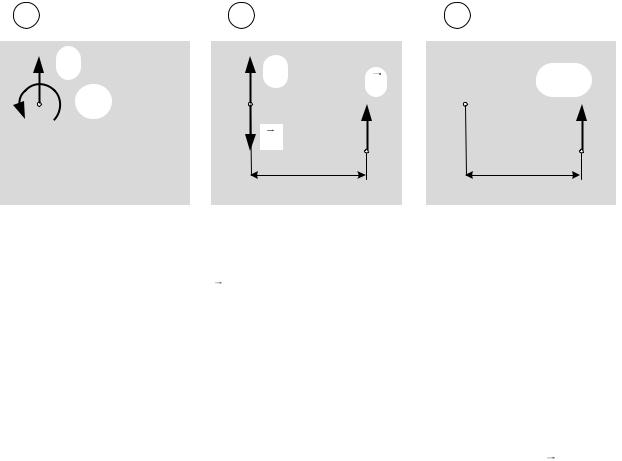
Рассмотрим последний случай подробнее (рис. 8.2).
Так как элементы пары можно изменять, сохраняя при этом ее момент, расположим пару (, ′), момент которой равен главному моменту системы
сил следующим образом:
68
а |
б |
|
в |
|
R* |
* |
|
|
* |
|
R |
R |
R |
|
O MO* |
|
R R |
|
|
O |
|
O |
|
|
|
R |
A |
|
A |
|
|
|
||
|
|
h |
h |
|
Рис. 8.2
1. пусть одна из сил пары ( R ) будет приложена в точке О и направлена против силы (рис. 8.2, б);
2. пусть модули сил, составляющих пару, равны модулю главного вектора:
= ′ = , и тогда плечо пары будет равно = ⁄ .
3. Уравновешенную систему сил ′ и можно исключить.
Исходная система сил оказывается эквивалентной одной силе R , т. е. имеет равнодействующую (геометрически равную главному вектору), линия
действия которой проходит на расстоянии = ⁄ от центра О.
8.3. УСЛОВИЯ РАВНОВЕСИЯ ПЛОСКОЙ СИСТЕМЫ СИЛ
Поскольку плоская система сил является частным случаем произвольной пространственной системы сил, для нее справедливы те же условия уравновешенности, что и для пространственной системы.
|
|
∑ |
|
|
|
= 0 |
|
(а) |
|
||
|
|
|
=1 |
|
|
|
|
|
|
||
|
|
∑ |
|
|
|
= 0 |
|
(б) |
|
||
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
{ |
∑ |
|
|
|
= 0 |
|
(в) |
(7.4) |
||
|
|
=1 |
|
|
|
|
|
|
|||
|
|
∑ |
|
|
|
|
|
|
(г) |
|
|
|
|
=1 |
|
( ) = 0 |
|
||||||
|
|
|
|
|
|
|
|
|
|||
|
{ |
∑ |
|
|
|
|
|
= 0 |
(д) |
|
|
|
=1 |
|
|
( ) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
= 0 |
(е), |
|
|||
{ |
=1 |
( ) |
|
||||||||
|
|
|
|
|
|
|
|
|
|||
Пусть плоскость (рис. 8.1, а), в которой лежат линии действия сил
69
системы — это плоскость xy . Ось z перпендикулярна этой плоскости. Рассматривая шесть уравнений равновесия произвольной
пространственной системы сил (7.4), легко видеть, что в данном случае уравнения
∑ |
|
≡ 0, |
∑ |
|
|
|
∑ |
|
|
|
=1 |
=1 |
( ) ≡ 0, |
=1 |
( ) ≡ 0 |
||||||
|
|
|
|
|
|
|
|
превращаются в тождества, так как все силы перпендикулярны оси z и лежат в одной плоскости с осями x и y.
Таким образом, условия уравновешенности плоской системы сил в аналитической форме будут представлены только тремя уравнениями:
|
∑ |
|
= 0 |
|
(а) |
|
|
|
=1 |
|
|
|
|
|
∑ |
|
= 0 |
|
(б) |
|
|
=1 |
|
|
|
|
|
|
∑ |
|
|
|
= 0 |
(е) |
{ |
=1 |
( ) |
||||
|
|
|
|
|
||
Последнее уравнение для плоской системы сил принято записывать иначе. Вместо того чтобы говорить о «моментах сил относительно оси z , проходящей через некоторую точку О, говорят о «моментах сил относительно точки О» (см. § 5.6) и записывают последнее уравнение в виде:
∑=1 ( ) = 0
Тогда уравнения равновесия для плоской системы сил принимают вид:
|
∑ |
|
= 0 |
|
(а) |
|
|
|
|
=1 |
|
|
|
|
|
|
∑ |
|
= 0 |
|
(б) |
(8.1) |
|
|
|
=1 |
|
|
|
|
|
|
∑ |
|
|
|
= 0 |
(е) |
|
{ |
=1 |
( ) |
|
||||
|
|
|
|
|
|
||
ЭТО ПЕРВАЯ (ОСНОВНАЯ) ФОРМА УРАВНЕНИЙ РАВНОВЕСИЯ ПРОИЗВОЛЬНОЙ ПЛОСКОЙ СИСТЕМЫ СИЛ.
Она состоит из двух уравнений проекций сил на две проведенные произвольным образом перпендикулярные оси х и у и одного уравнения моментов сил относительно произвольной точки О плоскости ху.
Можно показать, что системе уравнений (8.1) равносильны еще две формы записей уравнений равновесия для плоской системы сил.
ВТОРАЯ ФОРМА УРАВНЕНИЙ РАВНОВЕСИЯ ПЛОСКОЙ СИСТЕМЫ СИЛ:
