10482

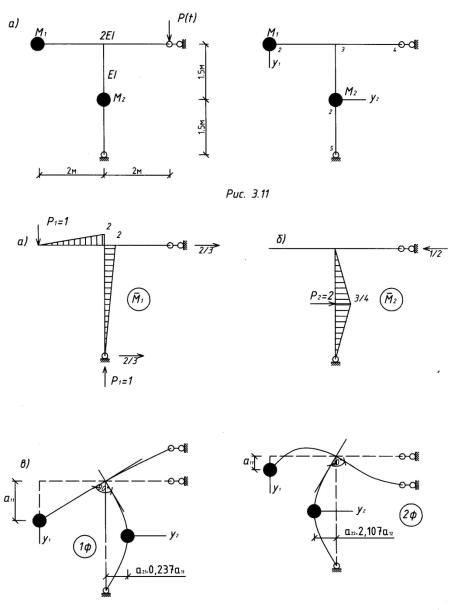
70

Рис.3.12

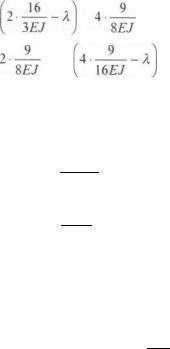
71

2. Строим эпюры изгибающих моментов от сил Р1 = 1, Р2 = 1, приложенных по направлению координат у1 и у2 (рис. 3.12. а, б).

Проверяем условие ортогональности (3.18):

2. 1. 1 + 4 . 0,237 . (-2,107) = 0,002. Погрешность 0,002/2 = 0,1% незначительна.

6.Строим собственные формы колебаний (рис. 3.12, в, г,).

7.Составляем уравнения движения системы (3.19):

y1 = a11 sin (ω1t+ α1) + al2 sin (ω2t +α2)

у2 = 0,237а11 sin (ω1t +α1) – 2,107a 12 sin (ω2t+ α2).

8.Определяем частоту гармонической нагрузки:

›0,8 ' 0,8 · 29,19 23,35 рад/с .

72

Рис.3.13

73

9.Строим эпюру изгибающих моментов от статического действия амплитуды гармонической нагрузки Р =6 кН (рис. 3.13, а).

10.Определяем перемещения от амплитудного значения гармонической

Составляем канонические уравнения (3.27):

12. 03,387 · 10YCÎ' 1,125 · 10YCÎ 0 24 · 10YC 0;

1,125 · 10YCÎ' 0 4,023 · 10YCÎ 0 6,75 · 10YC 0,

решением которых определяем амплитуды сил инерции:

Î' 07,3494 кН; Î 03,733 кН.

74

5. Определяем коэффициенты форм собственных колебаний и строим формы колебаний (рис. 3.4): φ11 =1; φ21 = 0 9384; φ12 =1; φ22 = 0,102 .

6. Составляем уравнения движения системы:

y1 = a11 sin (ω1t+ α1) + al2 sin (ω2t +α2)

у2 = -9,384а11 sin (ω1t +α1) + 0,102a12 sin (ω2t+ α2).

7.Определяем частоту гармонической нагрузки:

›0,8 ' 0,8 · 15,6 12,48 рад/с .

75

колебаний (рис. 3.15.в).

17. Составляем уравнения движения системы при вынужденных колебаниях

78

y1 = a11 sin (ω1t+ α1) + al2 sin (ω2t +α2)-0,0006241. sin ›&;

у2 = -9,384а11 sin (ω1t +α1) + 0,102a12 sin (ω2t+ α2)+0,01482. sin ›&.

Пример 3.5.3. Выполнить динамический расчет рам (рис. 3.16,а; 3.17, в) на действие гармонической нагрузки Р(t) = P sinθt, при Р = 8 кН, θ = 0,9ω1. Построить эпюры Mg, Qg, Ng. Результаты решения приведены на рисунках 3.16 и 3.17.

Пример 3.5.4. Выполнить динамический расчет рам (рис. 3.18, 3.19) на действие гармонической нагрузки P(t)-PSinθt, при Р=10kH θ=0,8ω)1. Построить эпюры динамических изгибающих моментов, поперечных и продольных сил самостоятельно.

4. КОЛЕБАНИЯ СИСТЕМ С БЕСКОНЕЧНЫМ ЧИСЛОМ

СТЕПЕНЕЙ СВОБОДЫ.

ПРИБЛИЖЕННЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ОСНОВНОЙ

СОБСТВЕННОЙ ЧАСТОТЫ КОЛЕБАНИЙ

Решение задачи о колебаниях системы с распределенной массой (с бесконечным числом степеней свободы) приводит в общем случае к сложным математическим выкладкам. При динамическом расчете сооружений на практике часто бывает достаточной оценка усилий, напряжений и деформаций, возникающих при главных колебаниях основного тона. Поэтому, широкое распространение получили приближенные методы (способы) определения основной (первой) собственной частоты колебаний. Из приближенных наиболее часто используются: энергетический метод; способ приведенной массы; способ замены распределенной массы сосредоточенными массами; способ Данкерлея.

При этом пренебрегают силами сопротивления и полагают, что колебания

79

отдельных точек системы (рис.4.1) около положения равновесия происходят по

и затем одновременно достигают крайних положений, где их скорости равны нулю, E 0, а потенциальная энергия становится П максимальной [5]