
10481
.pdf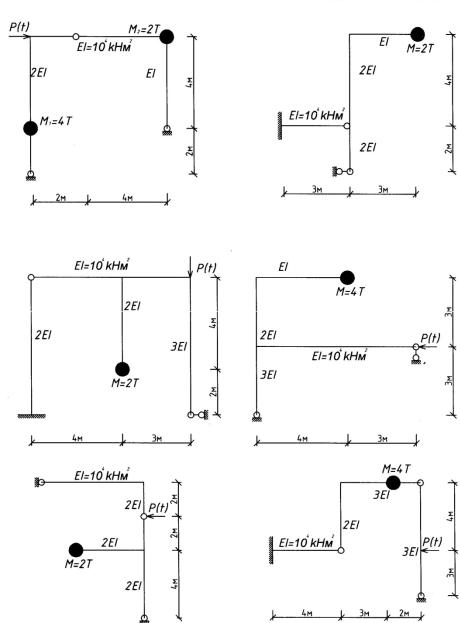
80
Рис.3.19

П |
|
= |
|
O |
|
81 |
|
|
|
|
|
[;\ |
|
ef |
Î RÎ |
|
|||||||
|
|
+ |
|
[ |
|
] |
2 . |
(4.4) |
|||
|
|
|
' |
Q |
|
|
|
|
|
||
Подставляя (4.3) и (4.4) в закон сохранения энергии |
П[;\ = E[;\ , получим |
||||||||||
формулу Рэлея для определения основной собственной частоты колебаний: |
|||||||||||
|
|
|
|
O |
Ú |
IP[ \ |
]- |
:\ |
(4.5) |
||
|
= O!Ú![ \ - \ :\ . |
|
|||||||||
При подстановке в (4.5) точного выражения формы колебаний, получим точное значение собственной частоты. Однако, в большинстве случаев, уравнение формы колебаний заранее неизвестно и его задают приближенно. Принимаемая для решения форма собственных колебаний основного тона должна отвечать граничным условиям и не иметь узловых точек. Обобщая (4.5) на системы с распределенной массой m(x) и n сосредоточенными массами ^ , $ = 1,2 … % , получим I формулу
Рэлея: |
|
|
O!Ú IP[ \ ]-:\ |
|
|
|
|
|
|
|
|
, |
(4.6) |
||
|
= O!Ú [ \ - \ :\1∑rÛ)m |
*r - \r |
|
||||
где Î^ - амплитуда колебаний точки с массой ^ в соответствии с принятой формой колебаний Î .
Уравнение формы собственных колебаний Î удобно принимать подобным уравнению прогиба системы от статической нагрузки g Î = g ∙ m x , то есть от действия сил тяжести, соответствующих массе системы. В этом случае получим
II формулу Рэлея: |
Oã |
ß à á à âà1∑rÛ)m |
*r \r |
|
|
||||
= g |
. |
(4.7) |
|||||||
Ú ! |
|
- |
m |
|
- |
\r |
|
||
|
O! [ \ |
|
\ :\1∑rÛ) *r |
|
|
|
|||
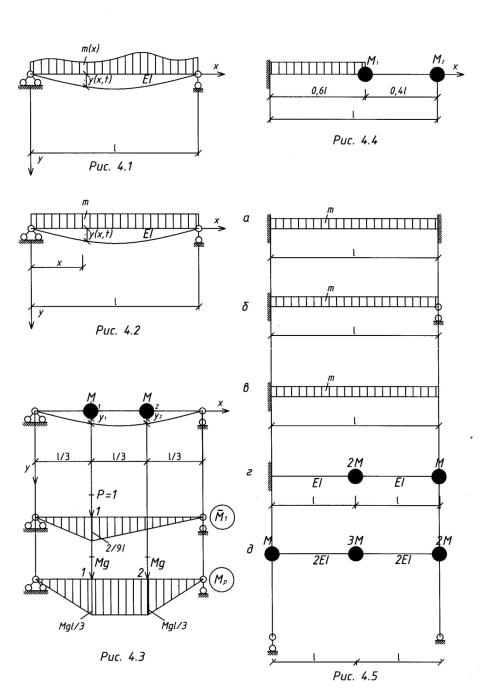
Пример 4.1.1. Определить основную собственную частоту колебаний простой балки с равномерно-распределенной массой (рис. 4.2).
Решение.
а). Зададим форму собственных колебаний точным уравнением:
Î = ]'#$% Q Î.
Вычислим интегралы, входящие в (4.5):
O+Q ef[ Î] RÎ = ]' QFF O+Q #$% Q ÎRÎ = ]' ∙ QFF ∙ Q ,
82
Q |
|
|
Q |
|
|
∙ |
3 |
. |
ä |
Î R Î = ]' |
ä #$% |
3 |
ÎRÎ = ]' |
2 |
|||
+ |
|
|
+ |
|
|
|
||
Тогда, согласно (4.5), |
будем иметь: |
= Q-- IP[ = ½,VH½HQ- IP[ . |
||||||
Получено точное значение основной собственной частоты, так как уравнение собственной формы колебаний задано точно.
б). Зададим форму собственных колебаний в виде уравнения прогиба от |
||||||||||||||||
статической нагрузки å = Ùg : Î = CIPæ 35Î − 23Î5 + ÎC . |
|
|
|
|
|
|
||||||||||
Вычислим интегралы, входящие в (4.7): |
|
|
|
|
|
|
|
|
||||||||
äQy x dx = |
å |
|
Q |
|
|
|
qlM |
, |
|
|
|
|
|
|||
|
ä l5x − 2lx5 + xC dx = |
|
|
|
|
|
||||||||||
+ |
|
|
|
24EI |
+ |
Q |
|
|
24EI ∙ 5 |
|
å |
|
|
31 |
|
|
äQ Î RÎ = ¶ |
|
|
Î − 23Î5 |
+ ÎC RÎ = ¶ |
|
· |
3½ . |
|||||||||
|
å · ä 35 |
|
||||||||||||||
+ |
|
|
|
|
24ef |
+ |
|
|
|
|
24ef |
|
630 |
|
||
Тогда, согласно (4.7), получим: |
|
ef |
|
9,88 |
|
ef |
|
|||||||||
|
|
= |
24ef ∙ g ∙ 630 ∙ 3M |
= 97,55 |
; = |
|
|
|||||||||
|
|
Ùg ∙ 31 ∙ 5 ∙ 3½ |
Ù3C |
|
3 |
BÙ . |
|
|||||||||
Погрешность |
решения б) |
в сравнении |
с решением |
|
а) |
составляет 0,105%. |
||||||||||
Формула Рэлея всегда дает несколько завышенное значение собственной частоты.
Пример 4.1.2. Определить основную собственную частоту колебаний простой
балки с двумя сосредоточенными массами (рис. 4.3).
Решение. Зададим форму собственных колебаний в виде уравнения прогиба от статической нагрузки j = Ù g и для определения ' и , входящих в (4.7),
построим эпюры изгибающих моментов от нагрузки и от силы j = 1 (рис. 4.3).
Используя правило перемножения1 2 3 2 g3эпюр1 Верещагина1 1 3 ,2 будемg3 иметь1 :
' = = 2 ∙ 9 3 ∙ 3 ∙ 3 ∙ 3 ∙ ef + 2 ∙ 9 3 ∙ 3 ∙ 3 ∙ 3 ∙ ef + + 3g3 ∙ 33 ∙ 32 ∙ 93 ∙ ef1 = 1625 ∙ efg35 .
83

|
|
|
|
|
|
|
|
|
84 |
|
|
|
|
|
Тогда: |
|
|
5 |
|
|
g35 |
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
∙ 2 |
|
|
|
|
|
|
|||
|
|
|
|
|
162ef |
|
|
ef |
||||||
|
|
162 |
ef |
|
|
|
= 5,69B |
|||||||
|
|
= g |
5 |
∙ |
g35 |
³ |
|
= |
5 35 |
; |
35 |
. |
||
|
|
|
M ±162 |
|
ef |
∙ 2 |
|
|
|
|
|
|
||
Получено точное значение основной собственной частоты.
Пример 4.1.3. Определить основную собственную частоту колебаний консольной балки (рис. 4.4) жесткостью EI, пролетом l с
равномерно-распределенной массой m и двумя сосредоточенными массами
' = 0,5Ù3, = 0,2Ù3 .
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
\ |
· |
|
|
Задаем форму собственных колебаний уравнением |
|
|
|
|
|
|
|
. |
|
|||||||||||||||||
Вычисляем интегралы, входящие в (4.5): |
Î |
|
'' |
|
|
|
= ]' ¶1 − ×# Q |
|
|
|||||||||||||||||
Q |
|
|
|
|
|
Q |
|
RÎ = |
3,038 |
|
|
|
|
|
||||||||||||
ä[ Î] RÎ = ä ì]' ¶1 − ×# |
23 |
|
· |
|
í |
|
|
3 |
5 |
]' ; |
|
|
|
|
||||||||||||
+ |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
Î |
|
|
|
|
|
|
|
|
|
|||
+,HQ |
Ù Î |
|
|
|
+,HQ |
¶1 |
|
|
− ×# |
·ï |
|
|
|
|
|
|
|
; |
||||||||
ä |
|
|
Î RÎ = ä Ù î]' |
|
|
23 |
|
RÎ = 0,536Ù3]' |
||||||||||||||||||
+ |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0,63 = ì]' ±1 − ×# |
∙ 0,63 |
³í |
|
|
|
; |
|
|
|
|||||||||||||
' |
Î = ' |
|
|
23 |
|
|
|
= 0,1698]' |
|
|
|
|||||||||||||||
|
|
|
|
|
3 = ì]' ±1 − ×# |
3 |
³í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Î = |
23 |
|
= ]' . |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Подставляем полученные величины в (4.5) и определяем основную собственную
частоту: |
|
|
|
3,038 ∙ A'/35 |
|
3,038ef C |
|
efC |
|
= ef |
|
= |
= 3,701 |
; |
|||||
|
0,536Ù3]' |
+ 0,5ml ∙ 0,1698A' + 0,2ml ∙ A' |
0,8209Ù3 |
|
Ù3 |
|
|||
|
|
ef |
|
|
|
|
|
|
|
= 1,924BÙ3C . |
|
|
|
|
|
|
|||
Пример 4.1.4. Определить самостоятельно основную собственную частоту
колебаний следующих систем (рис. 4.5), задаваясь формой собственных колебаний в

виде уравнения прогиба
-в схеме «а»: Î
-в схеме «б»: Î
-в схеме «в»: Î
-в схемах «г» и «д»:
85
от статической нагрузки å = Ù g :
= æQCIP- Î ¶1 − 2 \Q + \Q--· ;
= CVIPæQ- ¶5 \Q99 − 2 \QFF − 3 \Q--· ;
= HæQ- ¶Î − ' \F· ;
C+IP H Q- j = ∙ g
от статической нагрузки .
Результаты решения: |
|
|
|
|
|
|
||||
а) = 22,45 |
[QIPF |
; |
б) = 15,45 |
[QIPF |
; в) = 3,59 |
[QIPF |
; |
|||
г) = 0,56 |
*QIP9 |
; |
д) = 0,498 |
*QIP9 |
. |
|||||
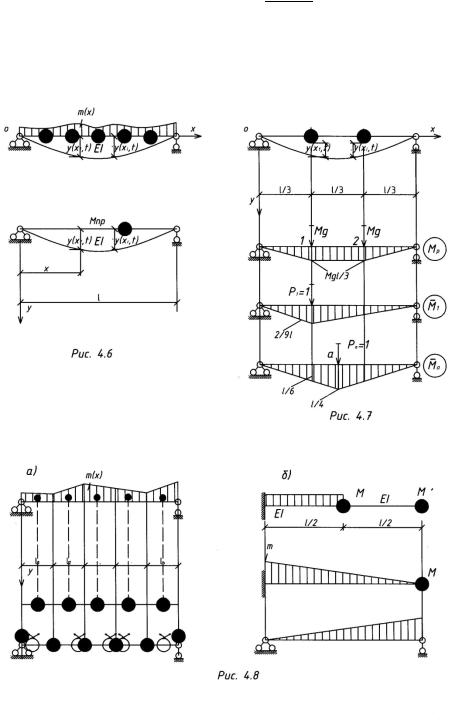
4.2.Способ приведенной массы
Вэтом способе система с распределенной массой Ù\ и n сосредоточенными массами ^ (i=1,2,… n) (рис. 4.6) заменяется системой с одной степенью свободы,
пр , сосредоточенную в произвольной точке «а». Законы движения
таких систем описываются уравнением в форме Фурье [5]: |
|
Î, & = Î & , |
(4.8) |
где & - функция, определяющая движение системы во времени, а сами системы |
|
считаются динамически эквивалентными. При таком условии, системы должны |
||||||||
иметь одинаковые кинетические энергии E в любой момент времени [5], то есть |
||||||||
e = |
1 |
|
Q |
|
s |
|
Î^ ô |
4.9 |
2 |
, & òä Ù Î |
|
Î RÎ + ó ^ |
|
||||
|
|
+ |
|
^t' |
|
|
|
|
для заданной системы и
e = ' пр ∙ ; ∙ , &
для системы с одной степенью свободы.
Приравнивая (4.9) и (4.10), получаем
пр = ; = O+Q Ù Î Î
и основной собственной частоты
выражение приведенной массы
RÎ + ∑s ^ Î^
; ^t'
(4.10)
4.11
86 |
|
|
1 |
, |
4.12 |
= B ;c;; |

87
где õ ö – уравнение собственной формы колебаний; õ öˆ и õ÷ - ординаты формы собственных колебаний в точках, соответственно, где сосредоточена масса
…ˆ и приведенная …÷ ; ø÷÷ - удельное перемещение в точке ÷, где сосредоточена приведенная масса …÷.
Пример 4.2.1. Определить основную собственную частоту колебаний простой балки с равномерно-распределенной массой (рис. 4.2).
Решение.
а) Приведем массу в середину пролета и зададим форму собственных колебаний
точным уравнением: ˜
õ ö = ùÔ‡ˆ‰ ú ö.
Вычислим интеграл, входящий в (4.11):
ú |
• |
|
|
• |
ú |
‡ˆ‰ |
˜ |
|
• |
ûú |
, |
|
ä û ö õ |
ö Œö = ûùÔ |
ä |
ú |
öŒö = ùÔ |
• |
|||||||
• |
•ú и ø÷÷: |
|
|
• |
|
|
|
|
|
|||
а также õ÷ при ö = |
˜ |
ú |
|
|
|
|
|
ú— |
|
|
||
Тогда: |
õ÷ = ùÔ‡ˆ‰ ú |
∙ • = ùÔ , |
ø÷÷ = üÓýþ . |
|
|
|||||||
…÷ = ù•∙ùÔ• ∙ûúÔ• |
= ûú• , † = Ô∙•∙üÓýþû∙ú∙ú— |
= |
,ú• Ó |
ýþû . |
|
|
||||||
Погрешность решения 0,72% в сравнении с точным решением, приведенным в примере 4.1.1 а.
б) Приведем массу в середину пролета и зададим форму собственных колебаний |
|||||||||||||||||||||
уравнением: |
õ ö = •üýþÑ ú—ö − •úö— + öü . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Вычислим интеграл, входящий в (4.11): |
|
|
|
|
Ñ |
|
|
—Ô |
|
|
|
||||||||||
ú |
• |
ö Œö = û ¶ |
Ñ |
· |
• ú |
— |
|
— |
ü |
• |
Œö = û |
¶ |
· |
• |
ú |
|
, |
||||
ä û ö õ |
|
•üýþ |
ä ú |
|
ö − •úö |
+ ö |
|
•üýþ |
|
|
—• |
|
|||||||||
• |
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а также õ÷ при ö = •ú |
и ø÷÷: |
|
|
|
|
Ñ |
|
|
ú— |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Ñúü |
|
|
ú |
ü |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
õ÷ = —Óüýþ = Ô |
|
∙ •üýþ |
, ø÷÷ = üÓýþ . |
|
|
|
|
|
|
|
|
|
|||||||

|
|
Ñ |
• —Ô |
|
|
|
88 |
|
|
|
|
|
Тогда: |
|
|
|
|
|
|
|
|
|
|
||
…÷ = |
û ¶•üýþ· |
∙ —• ú |
= •, |
|
•— |
|
|
üÓýþ |
|
, |
ýþ |
|
¶ |
Ñ ·• ∙ |
¶ úü·• |
|
|
ûú , † = B•, •— ûúü = |
ú• |
Bû . |
|||||
|
|
•üýþ |
Ô |
|
|
|
|
|
|
|
|
|
Погрешность решения составляет 1,11% в сравнении с точным решением,
приведенным в примере 4.1.1 а.
Пример 4.2.2. Определить основную собственную частоту колебаний простой балки с двумя сосредоточенными массами (рис. 4.7).
Решение.
Зададим форму собственных колебаний в виде уравнения прогиба от статической нагрузки j = Ù g и для определения ' и , ; и c;;, входящих в
(4.11) и (4.12), построим эпюры изгибающих моментов от нагрузки и от сил j = 1 и j; = 1 (рис. 4.7).
|
|
|
|
|
|
|
1 2 3 2 g3 1 |
|
1 1 |
3 2 g3 1 |
|
|
|
|
|
||||||||||||||||||||||
Используя правило перемножения эпюр Верещагина, |
будем иметь: |
||||||||||||||||||||||||||||||||||||
' = = |
2 ∙ |
9 3 ∙ |
3 |
∙ 3 |
∙ 3 |
|
∙ ef + |
2 |
∙ 9 |
3 ∙ 3 ∙ 3 ∙ 3 |
|
∙ ef + |
|
|
|
|
|
||||||||||||||||||||
|
|
|
+ |
g3 |
3 |
|
∙ |
3 |
3 |
|
1 |
= |
5 |
|
|
g35 |
; |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Ô |
|
3 |
|
∙ 3 |
2 |
∙ 9 |
∙ ef |
162 ∙ |
ú |
ef |
ú |
|
… ú |
|
Ô |
|
•—… ú— |
||||||||||||||||||
õ÷ = |
|
ú |
∙ |
ú |
• |
∙ |
|
… ú |
|
|
Ô |
Ô |
|
|
|
ú |
|
|
|
||||||||||||||||||
• |
∙ — |
∙ — |
|
|
— |
∙ • ∙ ýþ |
+ • ± |
+ ü³ ∙ ∙ |
— |
∙ • ∙ = ü ∙ Ô •ýþ . |
|||||||||||||||||||||||||||
Тогда: ø÷÷ = |
Ô |
|
ú |
|
ú |
• |
|
|
ú |
|
Ô |
|
|
ú— |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
• ∙ |
ü |
∙ • ∙ |
— |
∙ ü ∙ ýþ ∙ • = üÓýþ . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
± |
|
|
|
|
∙ |
|
— |
|
• |
∙ • |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
³ |
|
|
|
|
|
|
|
|
|
|
üÓýþ |
|
|
|
|
|
||||||||||||
…÷ = |
|
Ô |
|
• |
|
|
|
|
|
|
|
|
= Ô, |
Ô•— |
; |
|
|
||||||||||||||||||||
± |
|
|
∙ |
|
— |
|
• |
|
|
|
|
|
|
|
= BÔ, Ô•—…ú— = |
, |
|
—B ú— . |
|||||||||||||||||||
|
|
•— |
|
|
|
³ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Погрешностьü ∙ Ô |
решения• |
в сравнении с примером 4.1.2 составляет 1,05%. |
|||||||||||||||||||||||||||||||||||
Если привести обе сосредоточенные массы в точку «1» или «2», то погрешность
= , Ô• .
будет больше и составит 3,13%, так как в этом случае ú—
Пример 4.2.3. Определить основную собственную частоту колебаний
консольной балки (рис.4.4) с распределенной по длине массой m и

89
сосредоточенными массами ' = 0,5Ù3 и = 0,2Ù3 .
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а). Зададим форму собственных колебаний уравнением õ ö = ùÔ ¶Ô − ‡ ˜ö•ú · |
||||||||||||||||||||||||||
и приведем все массы в точку …Ô. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Вычислим интеграл в (4.1): |
+,HQ |
|
|
|
|
Î |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
+,HQ |
Ù Î |
|
Î RÎ = |
Ù î]' ¶1 |
− ×# |
·ï |
|
|
|
|
, |
|||||||||||||
|
|
|
ä |
|
|
ä |
|
23 |
|
RÎ = 0,536Ù3]' |
|||||||||||||||||
|
|
|
+ |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
и õÔ• ö = õÔ• •, ú = •, Ô ÓùÔ• |
, õ•• ö = õ•• ú = ùÔ• . |
|
|
|
|
|
||||||||||||||||||||
|
|
ø÷÷ = |
•, ú — |
= •, • |
|
• |
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Тогда: |
|
—ýþ |
|
ýþ . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
…÷ = |
•, — ûúùÔ• + •, ûú ∙ •, Ô ÓùÔ• + •, •ûúùÔ• |
= ü, Ó—ü |
|
ûú |
|
|||||||||||||||||||||
и, |
|
|
|
|
|
|
|
•, Ô ÓùÔ• |
= Ô, |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
= Bü, Ó—ü ûú ∙ •, • •ú— |
|
|
B úü . |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
ýþ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
б). Приведем все массы в точку …• . В результате решения задачи получим:
= Ô, Ô•B úü .
Пример 4.2.4. Определить самостоятельно основную собственную частоту колебаний следующих систем (рис. 4.5), задаваясь формой собственных колебаний аналогичными примеру (4.1.4), и приводя распределенную и сосредоточенные массы в середину пролета в схемах «а» и «б», на конец консоли в схемах «в» и «г»
и в левый или правый узел в схеме «д».
Результаты решения: |
|
|
|
|
|
|
||||
а) = 21,74 |
[QIPF |
; |
б) = 15,08 |
[QIPF |
; в) = 3,66 |
[QIPF |
; |
|||
г) = 0,55 |
*QIP9 |
; |
д) = 0,494 |
*QIP9 |
. |
|||||
