
10364
.pdf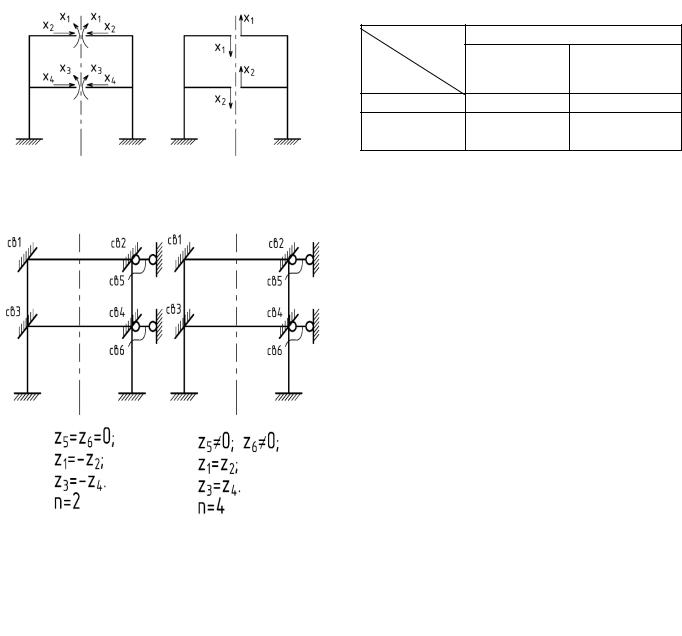
51 |
|
|
|
|
|
Таблица 5.1. |
|
Нагрузка |
Число неизвестных |
||
|
Симметричное |
Асимметричное |
|
Метод |
загружение |
загружение |
|
расчета |
|
|
|
Метод сил |
4 |
2 |
|
Метод |
2 |
4 |
|
перемещений |
|||
|
|
||
Из таблицы видно, что при расчете симметричных систем от действия симметричной нагрузки, целесообразно использовать метод перемещений, а при обратно симметричном загружении – метод сил.
Таким образом, расчет симметричных систем при действии произвольной нагрузки целесообразно выполнять по следующему алгоритму:
-разложить действующую нагрузку на симметричную и обратно симметричную;
-выполнить расчет заданной системы на действие симметричной нагрузки, используя метод перемещений;
- выполнить расчет заданной системы на действие обратно симметричной нагрузки,
используя метод сил; - выполнив наложение (суммирование)
результатов двух расчетов получим окончательный результат расчета на действие заданной на систему нагрузки.
Дальнейшее упрощение расчета симметричных систем можно получить путем членения заданной системы на симметричные части. При этом, все симметричные системы можно разделить на два вида:
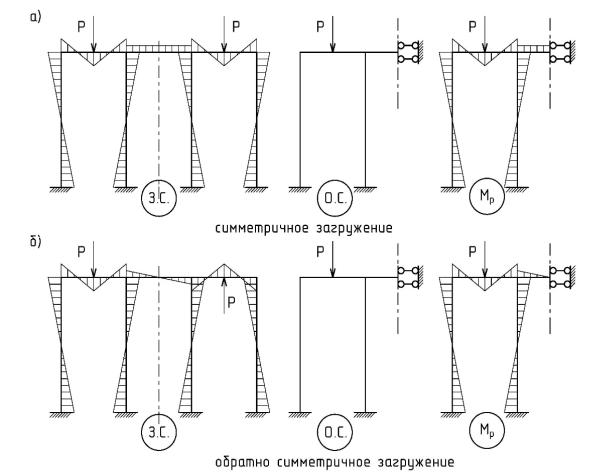
системы, у которых центральные оси сечения не одного из стержней не совпадают с осью симметрии заданной системы (рис. 5.7).
52
Рис. 5.7
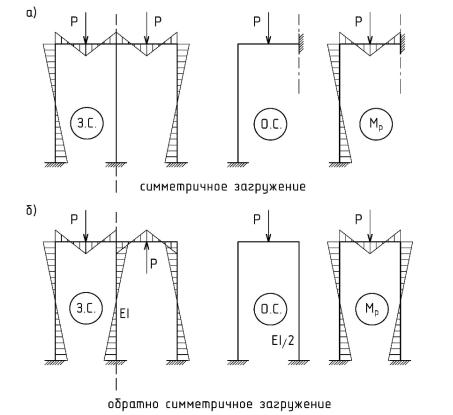
системы, у которых центральная ось одного из стержней совпадает с осью симметрии заданной системы (рис. 5.8).
53
Рис. 5.8
Задания для самостоятельной работы.
Литература: [1, гл. 8]; [2, гл.7];
Вопросы для самопроверки:
1.Какие системы относятся к симметричным?
2.Основные свойства симметричных систем при симметричной нагрузке. 3.Основные свойства симметричных систем при обратно симметричной нагрузке. 4.В чем суть комбинированного метода?
Задача 1. Выполнить расчет статически неопределимых симметричных рам (рис.4.16;
4.17) от нагрузки комбинированным методом и построить эпюры изгибающих момен-
тов самостоятельно.
6. Смешанный метод расчета
Смешанный метод расчета был предложен и разработан профессором А. А. Гвоздевым в работе “Общий метод расчета статически неопределимых систем” (1927 г.). В этой работе А. А. Гвоздев рассмотрел методы сил и перемещений как частные случаи единого общего метода – смешанного метода расчета.
При расчете статически неопределимых систем широко используются и метод сил и метод перемещений. При этом определяющим выбор того или иного метода расчета является число неизвестных – лишних связей по методу сил и возможных угловых и линейных перемещений узлов системы по методу перемещений.
54
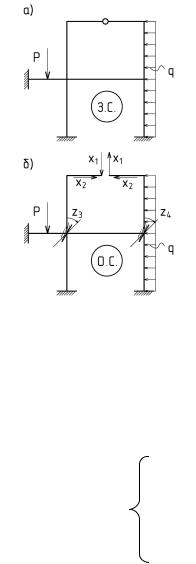
Однако для ряда статически неопределимых систем при вычислении усилий в ее элементах оказывается целесообразным совместное использование обоих методов сразу. Рассмотрим статически неопределимую раму, изображенную на рис. 6.1.
Общее число неизвестных:
-по методу сил: Л = 3 . 3 – 1 = 8 ;
-по методу перемещений: n = 4 + 2 = 6.
С другой стороны, можно видеть, что верхняя часть системы более тяготеет к методу сил, а нижняя – к методу перемещений. Выбирая основную систему из заданной путем устранения n1 лишних связей из верхней части системы, которую удобнее рассчитывать методом сил, и введением n2 связей в нижней части системы, для которой рациональней использовать метод перемещений,
мы получаем основную систему смешанного метода расчета (рис. 6. 1б ).
При этом, устранение связей не должно приводить к Рис 6.1 подвижности звеньев системы, а введение дополнительных связей должно обеспечивать в этой части системы закрепление свободных жестких узлов
от угловых и линейных смещений и шарнирных узлов от линейных смещений. Выбранная основная система отличается по своему состоянию от заданной. Для
приведения ее работы к работе заданной системы составляем канонические уравнения смешанного метода расчета:
|
11 |
x |
12 |
x |
2 |
* |
z |
3 |
* |
|
|
z |
4 |
|
|
1P |
|
0 ; |
||||||
|
|
1 |
|
|
13 |
|
|
14 |
|
|
|
|
|
|
|
|||||||||
|
21 |
x |
22 |
x |
2 |
* |
z |
3 |
* |
|
|
z |
4 |
|
2P |
0 ; |
||||||||
|
1 |
|
23 |
|
|
24 |
|
|
|
|
|
|
||||||||||||
|
r* |
x r* |
x |
2 |
r |
z |
3 |
r |
z |
4 |
|
R |
|
|
0 ; |
|||||||||
|
|
31 |
1 |
|
32 |
|
33 |
|
34 |
|
|
|
|
|
|
3P |
|
|
||||||
|
r* |
x r* |
x |
2 |
r |
z |
3 |
r |
|
z |
4 |
|
R |
|
|
0 . |
||||||||
|
|
41 |
1 |
|
42 |
|
43 |
|
44 |
|
|
|
|
|
4P |
|
|
|||||||
Из уравнений видно, что они имеют смешанный характер: первые два из них (в
общем случае их число n1) имеют геометрический смысл, так как выражают отсутствие перемещений точек приложения устраненных связей основной системы; вторые два уравнения (в общем случае их число n2 ) имеют статический смысл, так как выражают отсутствие реакций во введенных связях основной системы.
Неизвестными уравнений являются с одной стороны усилия xi , а с другой стороны перемещения zk . Коэффициенты при неизвестных представляют собой удельные перемещения и удельные реакции следующих видов:
ii - главное удельное перемещение;
ij - побочное удельное перемещение;
in* - побочное удельное перемещение точки приложения лишнего неизвестного xi
по его направлению от смещения связи n на единицу ( zn 1);
55
rnn - главная удельная реакция;
rnk - побочная удельная реакция;
rni* - побочная удельная реакция в связи n, вызванная действием единичного
усилия xi 1.
Удельные реакции и удельные перемещения обладают свойством взаимности на основании:
- первой теоремой Релея: rnn rnm ;
- теоремы Максвелла: ij |
ji ; |
- теоремы Гвоздева (или 2-ой теоремы Релея): rni* in* .
Определив неизвестные xi и zk из канонических уравнений смешанного метода,
далее несложно |
определить внутренние усилия MP , QP , NP в заданной системе от |
||||||
заданной нагрузки: |
|
|
|
|
|
||
|
|
|
|
n |
___ |
k |
___ |
|
|
|
|
MP MPo Mmno xi Mmn* zi ; |
|||
|
|
|
|
i 1 |
|
i n 1 |
|
|
|
|
|
n |
___ |
k |
___ |
|
|
|
|
QP QPo Qmno xi Qmn* zi ; |
|||
|
|
|
|
i 1 |
|
i n 1 |
|
|
|
|
|
n |
___ |
k |
___ |
|
|
|
|
NP NPo Nmno |
xi Nmn* zi . |
||
|
|
|
|
i 1 |
|
i n 1 |
|
В этих выражениях: |
|
|
|
||||
MPo ,QPo , NPo - |
изгибающий момент, |
поперечная и продольная силы от заданной |
|||||
нагрузки в основной системе смешанного метода; |
|
||||||
___ |
___ |
___ |
|
|
|
|
|
Mo |
,Qo |
, No |
- |
внутренние усилия в основной системе смешанного метода от |
|||
mn |
mn |
mn |
|
|
|
|
|
единичного значения лишнего неизвестного xn 1; |
|
||||||
___ |
___ |
___ |
|
|
|
|
|
M* |
,Q* |
, N* |
- |
внутренние усилия в основной системе смешанного метода от |
|||
mn |
mn |
mn |
|
|
|
|
|
единичного смещения введенной связи zn 1.
Задания для самостоятельной работы.
Литература: [1, гл. 8]; [2, гл. 8];
Вопросы для самопроверки:
1.Какие величины являются основными неизвестными смешанного метода?
2.Как формируется основная система смешанного метода?
3.Из каких условий получаются канонические уравнения смешанного метода? 4.Свойства и способы определения коэффициентов канонических уравнений смешан-
ного метода?
5.Как по найденным основным неизвестным смешанного метода вычисляются искомые усилия в заданной системе?
56
7. Определение перемещений в статически неопределимых системах
7.1. Перемещение от нагрузки
Существуют три разновидности формул, позволяющие определять перемещения точек (узлов) статически неопределимых систем по заданному направлению от внешней нагрузки.
Первая запись формулы идентична формуле определения перемещений, полученной для статически определимых систем, и имеет следующий вид:
|
l |
Mi |
MP |
|
|
iP |
|
dS, |
|||
|
|
||||
|
0 |
EI |
|||
|
|
|
|
||
__
где: Mi - изгибающий момент в статически неопределимой системе от единичного силового фактора Pi=1 (или Мi=1), приложенного в точке i по направлению изучаемого перемещения;
MP - изгибающий момент в статически неопределимой системе от заданной нагрузки.
Для определения перемещений по этой формуле необходимо дважды рассмотреть работу статически неопределимой системы: от единичного силового фактора Pi = 1 (или Mi =1 при определении углового перемещения) и от заданной нагрузки.
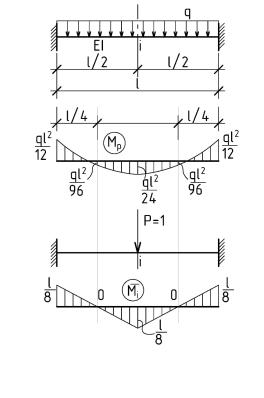
Пример 1 (рис. 7.1). Определить вертикальное перемещение точки i защемленного по концам стержня постоянной жесткости EI от равномерно распределенной нагрузки интенсивностью q.
Используя для перемножения эпюр формулу Симпсона, получим:
|
|
l |
|
MP |
|
|
|
|
L |
|
|
|
|
|
|
|
|
||
iP |
|
Mi |
dS |
|
( 0 4 1 2 )= |
|
|
||||||||||||
|
|
6 |
|
|
|||||||||||||||
|
|
0 |
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
q l2 |
|
l |
|
|
|
q l |
2 |
|
q l2 |
l |
|
|||
|
|
|
|
|
( |
|
|
|
|
4 |
|
|
0 |
|
|
|
) 2 |
||
|
2 6 EI |
12 |
8 |
96 |
|
24 |
8 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
q l4 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
384 EI
Здесь L - длина участка стержня, по которому ведется перемножение эпюр.
Рис. 7.1 Вторая запись формулы может быть получена из рассмотрения сравнения состояний
заданной статически неопределимой системы, находящейся под действием внешней нагрузки и статически определимой системы, нагруженной той же нагрузкой и полученной из заданной системы путем устранения всех избыточных связей.
Накладывая на статически определимую систему требование, чтобы она работала как заданная, можно записать следующее условие:

57
|
l |
M0 M0 |
(P,x ,x |
2 |
,...,x |
n |
) |
|
|
iP i0 (P, x1 , x2 ,..., |
xn ) или: iP |
i |
1 |
|
|
|
dS . |
||
|
EI |
|
|
|
|
|
|||
|
0 |
|
|
|
|
|
|
|
|
Учитывая, что изгибающий момент в любой статически неопределимой системе |
|||||||||
|
|
n |
|
|
|
|
|
|
|
определяется из выражения: |
M 0 (P,x1,x2,...,xn ) MP0 |
Mi0 |
xi , |
окончательно получим |
|||||
|
|
i 1 |
|
|
|
|
|
|
|
вторую разновидность формулы для определения перемещений от нагрузки в статически
|
|
l |
M0 M |
P |
|
неопределимых системах: |
iP |
0 |
i |
dS . |
|
EI |
|
Таким образом, при использовании этой формулы необходимо:
-построить эпюру изгибающих моментов в заданной статически неопределимой системе (MP);
-построить эпюру моментов в любой статически определимой системе, полученной из заданной путем устранения избыточных связей, от единичного силового фактора, приложенного в изучаемой точке в направлении изучаемого перемещения;
-выполнить перемножение эпюр.
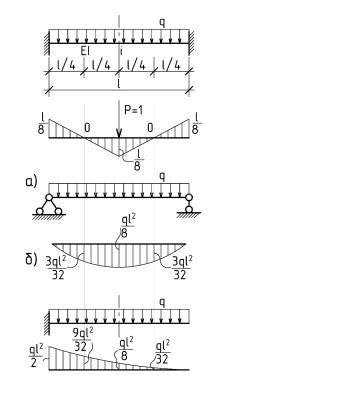
Пример 2 (рис. 7.2). Данные примера те же, что и в предыдущем случае (см. пример 1).
Для основной системы по рис. 7.2а будем иметь:
|
|
|
|
l |
|
|
q l2 |
|
l |
|
q l |
2 |
|
l |
|
q l2 |
|
|
iP |
|
|
|
( |
|
|
|
4 |
|
|
|
|
|
|
0) |
|
2 6 EI |
12 |
2 |
96 |
|
4 |
24 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
q l4 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
384 EI |
|
|
|
|
|
|
|
|
|
|
|
||
Для основной системы по рис. 7.2б получим:
|
iP |
|
|
l |
|
( |
q l2 |
0 4 |
q l2 |
|
l |
|
q l |
2 |
|
l |
) 2 |
2 6 EI |
|
12 |
96 |
8 |
24 |
|
4 |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
q l4 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
384 EI |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Третья запись формулы может быть получена при использовании принципа
пропорциональности, в соответствии с которым
iP iP P , где iP - удельное перемещение изучаемой точки i по изучаемому направлению в заданной статически неопределимой системе, вызванное единичными силовыми факторами. Его можно рассматривать как групповое перемещение, вызванное
|
l |
Mi |
MP |
l |
0 |
|
|
групповыми силовыми факторами (P=1), т.е. iP |
|
dS |
Mi |
MP |
dS . |
||
EI |
|
|
|||||
|
0 |
0 |
|
EI |
|||
|
|
|
|
|
|
||
58
l |
|
|
l |
0 |
|
|
Тогда: iP |
Mi |
P MP |
dS или |
iP |
Mi MP |
dS . |
|
||||||
|
|
|
||||
0 |
|
EI |
0 |
EI |
||
В этих выражениях: |
|
|
|
|
|
|
- MP0 - изгибающий момент от единичного значения внешних нагрузок в любой статически определимой системе, полученной из заданной путем устранения всех избыточных связей;
- MP0 - изгибающий момент от заданной нагрузки в любой статически определимой системе, полученной из заданной путем устранения всех избыточных связей;
- |
Mi - |
изгибающий момент от единичного силового фактора, приложенного в |
изучаемой |
точке |
в направлении изучаемого перемещения в заданной статически |
неопределимой системе. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3 (рис. |
7.3). Данные примера те же, что и в |
|||||||||||||||||||||||||||||||||
предыдущем случае (см. пример 1). |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Для основной системы по рис. 7.3а будем иметь: |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
l |
|
|
|
|
l |
|
|
|
|
|
|
3 q l |
2 |
|
|
l |
|
q l2 |
|
|
|
||||||||
|
iP |
|
|
|
|
|
|
( |
|
|
|
0 4 |
|
|
|
|
0 |
|
|
|
|
|
|
) 2 |
||||||||||
2 6 EI |
8 |
32 |
|
8 |
|
|
8 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
q l4 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
384 EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Для основной системы по рис. 7.3б будем иметь: |
||||||||||||||||||||||||||||||||||
|
iP |
|
|
|
l |
|
[( |
q l2 |
|
|
l |
4 |
9 q l2 |
0 |
|
q l2 |
|
l |
) |
|||||||||||||||
2 6 EI |
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 8 |
|
|
|
|
|
|
|
|
|
8 8 |
|
||||||||||||||
|
|
( |
q l2 |
|
l |
|
4 |
q l |
2 |
0 |
l |
0) |
|
|
q l4 |
. |
|
|
||||||||||||||||
|
|
8 |
|
8 |
|
32 |
|
8 |
|
384 EI |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Рис. 7.3
7.2. Перемещение от изменения температурного режима
Распространяя формулу определения перемещений от изменения температурного режима в статически определимых системах на системы статически неопределимые, получим первую запись формулы в виде следующего выражения:
|
|
l |
t |
___ |
l |
___ |
|
it |
|
Mi |
ds t0 Ni dS , |
||
|
h |
|||||
|
|
0 |
|
0 |
|
|
___ |
___ |
|
|
|
|
|
где: Mi |
, Ni - изгибающий момент и продольная сила в статически неопредели- |
|||||
мой (заданной) системе от единичного силового фактора Р = 1 (или M = 1 – если опреде-
59
ляется угловое перемещение), приложенного в изучаемой точке в направлении изучаемого перемещения.
Если по заданию требуется от изменения температурного режима определить перемещения нескольких точек, то становится необходимым выполнение такого же количества расчетов (равного количеству точек) статически неопределимой системы, загруженной в каждом варианте своим единичным силовым фактором, приложенным в соответствующей (изучаемой) точке.
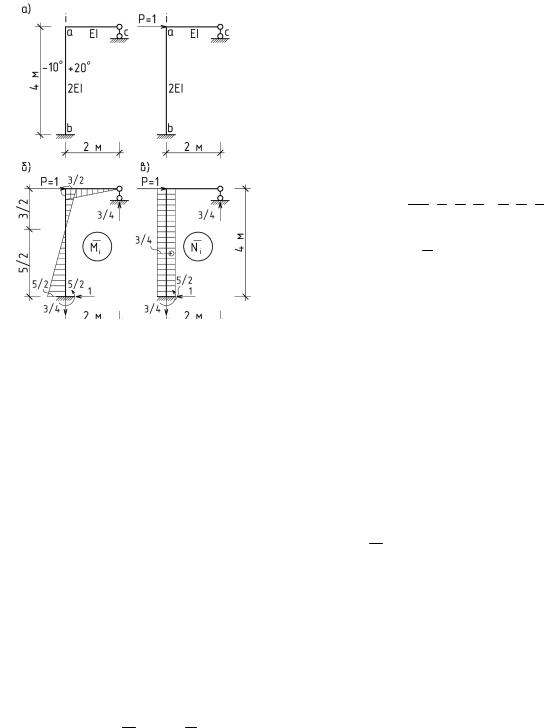
Пример. Определить горизонтальное перемещение точки i статически неопределимой рамы, изображенной на рис. 7.4, от температурного пе-
репада на стойке. Принять: 10 5 град 1 ,
h 0,5 см.
На рис. 7.4б и 7.4в показаны, соответственно, эпюры изгибающих моментов и продольных сил в заданной статически неопределимой системе.
it 10 5 30 (1 3 3 1 5 5) 0,5 2 2 2 2 2 2
10 5 5 3 4 1,05 10 2 м. 4
Вторая запись формулы может быть получена из рассмотрения сравнения состояний заданной статически неопределимой системы, находящейся под действием
изменения температурного режима и статически определимой системы, полученной из заданной путем устранения всех избыточных связей и находящейся под действием того же изменения температурного режима и, кроме этого, лишних неизвестных.
|
it |
0 |
(t, x |
, x |
,...,x |
) 0 |
i |
0 (x , x |
,..., x |
) |
|
|
|
|
|
||||||||
|
i |
1 |
|
2 |
|
|
n |
it |
|
1 2 |
n |
|
|
|
|
|
|
|
|
||||
|
|
|
l |
t |
|
|
|
|
|
|
l |
|
|
|
|
l |
|
0 |
M0 (x , x |
,...x |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
Mi0dS |
t0 Ni0dS |
|
i |
1 2 |
n |
|
dS. |
|||||||||||
|
|
h |
|
|
|
EI |
|
|
|||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
||
n
Но в этом выражении M 0(x1, x2,..., xn ) M 0j xj Mt . Поэтому окончательно
j 1
будем иметь следующее выражение для определения перемещений в статически неопределимых системах от изменения температурного режима:
l |
|
|
|
l |
|
l |
|
0 |
|
|
||
it |
t |
|
|
i0dS t0 |
|
|
Mi |
|
Mt |
dS. |
||
M |
Ni0dS |
|
||||||||||
h |
|
|
|
|||||||||
0 |
0 |
0 |
|
|
|
EI |
||||||
Из полученного выражения видно, что для его использования необходимо сначала выполнить расчет статически неопределимой системы от изменения температурного режима. Усилия Mi0 и Ni0 могут быть получены из рассмотрения условий равновесия
любой статически определимой системы, полученной из заданной.

60
Пример (см. рис.7.5). Данные примера те же, что и в предыдущем случае.
Каноническое уравнение метода сил:
11 |
x1 1t |
0, |
где: |
|
|
|
|
|
|
|||
11 |
2 4 2 |
1 |
|
1 |
2 2 |
2 |
2 |
1 |
|
10,667 |
; |
|
2EI |
|
3 |
EI |
|
||||||||
|
|
|
2 |
|
|
|
EI |
|||||
1t 10 5 30 (2 4) 10 5 5 (1 4) 0,05. 0,5
Тогда: x1 1t 0,05 EI 4,69 10 3 кН.11 10,667
Искомое горизонтальное перемещение точки i в заданной системе, вызванное изменением температурного режима, будет равно:
it 10 5 30 ( 1 4 4) 10 5 5 0
0.52
|
1 |
4 4 9,38 10 3 EI |
1 |
1,05 10 2 м. |
|
|
|||
2 |
|
2EI |
||
Рис 7.5
