10301

[Введите текст]

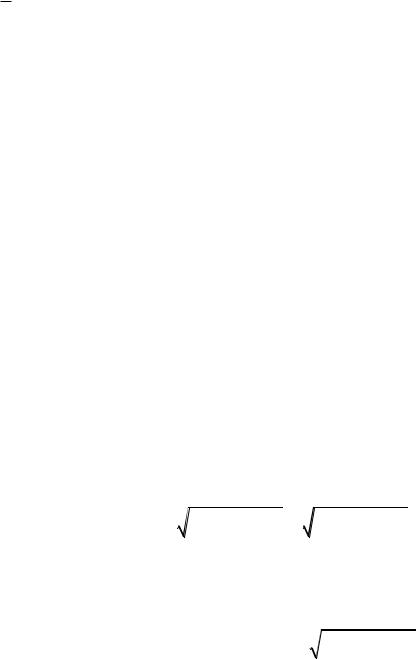
Выведем теперь уравнение эллипса. Для этого введём прямоугольную декартову систему координат. В качестве оси абсцисс мы возьмём прямую, проходящую через F1 и F2 , считая её направленной от F1 к F2 , начало

системы координат поместим в середине отрезка F1F2 (рис. 25.1).

Рис. 25.1

В этой системе координат для произвольной точки M координаты обозначим через x и y . Фокусы, оказавшись теперь на оси Ox

симметрично относительно начала, будут иметь координаты F1 c;0 и F2 c;0 . Расстояния MF1 и MF2 между точками заменим их выражениями через координаты. Получим

x c 2 y2 x c 2 y2 2a .

По существу, это соотношение представляет собой уравнение эллипса.Ему удовлетворяют координаты точек в том и только том случае, когда точки лежат на эллипсе. Проведём алгебраические преобразования, упрощающие эту запись. Для этого уединим в уравнении первый радикал, возведём в квадрат обе части полученного равенства

и приведём его к виду a x c 2 y2 a2 cx . Возведя в квадрат обе части последнего равенства, найдём

a2 c2 x2 a2 y2 a2 a2 c2 .

180

[Введите текст]

x2 y2 a2 . Чем ближе эксцентриситет к единице, тем меньше отношение

b и тем больше эллипс вытянут. a

25.2. Гипербола. Множество всех точек M плоскости, разность расстояний которых до двух данных точек F1 и F2 есть величина

постоянная, называется гиперболой. Указанная разность берётся по абсолютному значению и обозначается 2a . Точки F1 и F2 называются

фокусами гиперболы. Как и ранее, 2c F1F2 - расстояние междуфокусами.

После преобразований, аналогичных тем, которые были проделаны для уравнения эллипса, соотношение приобретает вид

Учитывая, что, в отличие от эллипса, для гиперболы a c , можно ввести

182

[Введите текст]

Это уравнение называется каноническим уравнением гиперболы.

Так как уравнение (25.3) содержит x и y только в чётных степенях, то гипербола симметрична относительно осей Ox и Oy , а также относительно

начала координат. Оси симметрии гиперболы называются её осями, а точка пересечения осей – центром гиперболы. Положив y 0 в уравнении (25.3),

найдём две точки пересечения гиперболы с осью Ox : A1 a;0 , A2 a;0 , которые называются вершинами гиперболы. Если взять x 0 в уравнении

что гипербола состоит из двух частей: её точки расположены справа от прямой x a , образуя правую ветвь, и слева от прямой x a , образуя левую ветвь. Наконец, из уравнения (25.3) видно, что с возрастанием x

неограниченная правая ветвь. При x от значения x a получается левая неограниченная ветвь гиперболы (рис. 25.2).

183

[Введите текст]

Рис. 25.2

Присмотримся более внимательно к тому, как именно точка M «уходит в бесконечность». В лекциях по математическому анализу было введено понятие наклонной асимптоты графика функции. Из уравнения

(25.3) выразим переменную y ba x2 a2 . Далее для полученных двух

функций используем формулы нахождения коэффициентов уравнения y kx d наклонной асимптоты при x

правой ветви гиперболы при x . Для левой ветви из соображений симметрии при x получаются те же асимптоты.

Итак, построение гиперболы по каноническому уравнению (25.3) следует начинать с изображения основного прямоугольника, продолжая

184

[Введите текст]

диагонали которого мы получим асимптоты. Обе бесконечные ветви рисуем неограниченно приближающимися к ним (рис. 25.2). Фокусы находятся на

прямоугольник равносторонней гиперболы становится квадратом; прямые y x и y x являются асимптотами, перпендикулярными друг к другу.

Отношение расстояния между фокусами к расстоянию между вершинами гиперболы называется эксцентриситетом гиперболы и

Следовательно, как и для эллипса, эксцентриситет гиперболы определяется отношением её осей. Он характеризует форму основного прямоугольника гиперболы. Чем меньше эксцентриситет, тем меньше

отношение ba , то есть основной прямоугольник более вытянут в направлении действительной оси. Для равносторонней гиперболы 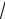2 .

Лекция 26. Парабола. Приведение кривых к каноническому виду

185

[Введите текст]

26.1. Парабола. Множество всех точек плоскости, равноудалённых от данной точки F (фокуса) и данной прямой L (директрисы), называется параболой. Расстояние от фокуса до директрисы параболы принято обозначать через p (рис. 26.1). Величину p называют фокальным

параметром параболы.

Для получения уравнения параболы необходимо ввести систему координат на плоскости. Проведём ось абсцисс через фокус параболы перпендикулярно директрисе, будем считать её направленной от директрисы к фокусу; начало координат расположим посередине между

директрисы равно MQ , где Q – основание перпендикуляра, опущенного из

[Введите текст]

Как для эллипса и гиперболы, уравнение параболы тоже является

частным случаем уравнения второго порядка. Оно получается из (25.1) при

A B D F 0.

Уравнение (26.1) содержит переменную y только в чётной степени, что доказывает симметрию параболы относительно оси Ox . Так как p 0 , то

переменная x должна быть неотрицательной. Это означает, что парабола расположена справа от оси Oy . Если x 0 , получаем

возрастании x возрастает и y (причём, если x , то y ). Построив в первой четверти график функции y 2 px и отразив его симметрично

относительно оси Ox , получим геометрическое изображение параболы (рис. 26.1). Ось симметрии параболы (в данном случае совпадающая с осью Ox ) называется её осью. Точка, в которой парабола пересекает свою ось, называется её вершиной (в нашем случае вершина совпадает с началом координат). Для описания геометрического смысла фокального параметра

расстояние между которыми равно 22 p . Тем самым, чем больше p , тем больше расстояние M1M 2 . Следовательно, параметр p характеризует

«ширину» области, ограниченной параболой.

Кроме рассмотренных классических кривых, уравнение линии второго порядка может привести ещё к нескольким геометрическим случаям, называемым вырожденными.

26.2. Вырожденные случаи. Если в уравнении линии второго порядка

коэффициенты B D E F 0 , то остаётся только два слагаемых, т.е. Ax2 Cy2 0 . При одинаковых знаках A и C уравнению соответствует на плоскости одна точка – начало координат. При разных знаках A и C – пара

то на плоскости получается одна прямая. Если B D E 0 и в уравнении

187

каноническому виду. Мы рассмотрели все геометрические ситуации, к которым может привести общее уравнение линии второго порядка (п. 26.2). В задачах аналитической геометрии обычно задаётся вид уравнения второго порядка с конкретными числовыми коэффициентами. В нём могут присутствовать произведение координат x и y (т.е. B 0 ) или переменные

x и y без квадратов ( D 0 или Е 0 ). Это будет означать, что в исходной

системе координат уравнение не является каноническим. Нужно перейти к другой системе координат, в которой уравнение будет иметь канонический вид. Это даст возможность определить, к какому из рассмотренных случаев относится заданное уравнение. После этого легко будет построить график заданной кривой.

Для приведения уравнения линии второго порядка к каноническому виду используются только те преобразования системы координат, которые не изменяют расстояния между точками, то есть не деформируют кривую. К таким преобразованиям, в частности, относятся параллельный перенос и поворот осей координат. Этих преобразований достаточно для решения поставленных в этой лекции задач. Разберём далее, что происходит с уравнениями при том или ином преобразовании координат.

26.4. Параллельный перенос осей координат. Рассмотрим на плоскости прямоугольную декартову систему координат xO y

[Введите текст]

переход от системы xO y к системе Oўxўyў называется параллельным

переносом осей координат.

Для произвольной точки M координаты относительно исходных осей обозначим через (x; y), а координаты по отношению к «новым» осям

189