
10291
.pdf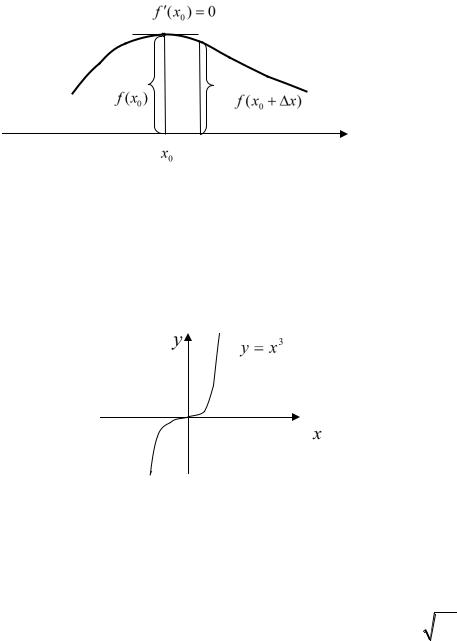
|
f (x x) f (x ) |
0, x 0 |
|
||
f (x0 ) lim |
0 |
0 |
|
|
f (x0 ) 0 . |
|
x |
x 0 |
|||
x 0 |
|
0, |
|
||
|
|
|
|
|
|
Рис.22.3
Следующий пример показывает, что обратное утверждение не верно. Так, для функции y x3 производная в начале координат равна нулю, касательная совпадает с осью абсцисс, но экстремума в этой точке нет.
Рис.22.4
Другие точки, в которых могут быть экстремумы, это точки, в которых производная либо не существует, либо обращается в бесконечность. В совокупности со стационарными эти точки называют критическими.
|
|
|
|
|
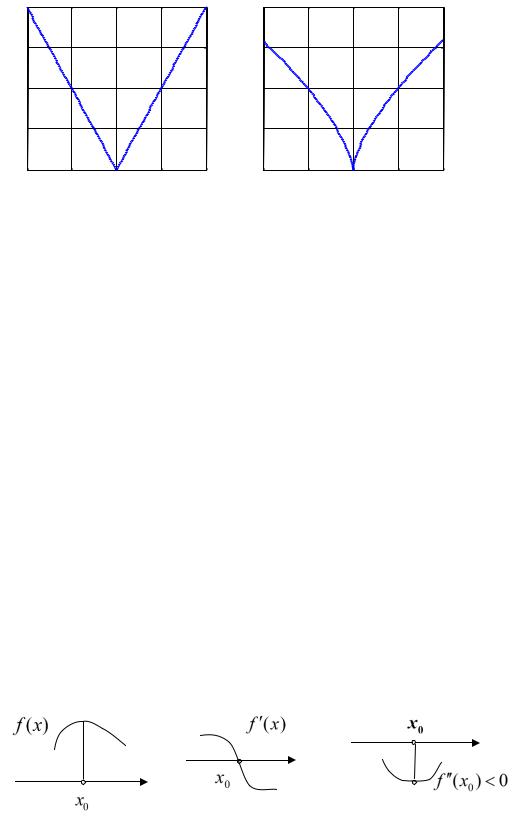
и y 3 x2 |
||
Примеры критических точек такого рода дают функции y |
x |
||
. |
|
|
|
160
2 |
|
|
|
|
2 |
|
|
|
|
1.5 |
|
|
|
|
1.5 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
0.5 |
|
|
|
|
0.5 |
|
|
|
|
0 |
-1 |
0 |
1 |
2 |
0 |
-1 |
0 |
1 |
2 |
-2 |
-2 |
||||||||
|
|
|
|
|
Рис. 22.5 |
|
|
|
|
Необходимые условия позволяют выделить точки, «подозрительные» на экстремум. Далее для каждой из них следует выяснить, есть ли экстремум в данной точке и, если есть, то каков он. Для этого существует следующие условия.
Достаточные условия экстремума.Если при «переходе» слева направо через критическую точку производная меняет знак с плюса на минус, то в этой точке максимум, а если с минуса на плюс, то минимум. Для дважды дифференцируемой функции это эквивалентно тому, что, если в стационарной точке x0 вторая производная отрицательна f (x0 ) 0 , то это
точка максимума, а если вторая производная положительна f (x0 ) 0 , то
это точка минимума.
В самом деле, смена знака производной означает переход функции от возрастания к убыванию или наоборот, что соответствует экстремуму. Для дважды дифференцируемой функции смена знакаиторой производной, например, с плюса на минус при переходе через стационарную точку означает, что первая производная функции убывает в некоторой окрестности этой точки. Следовательно, производная от первой производной, т.е. вторая производная f (x) , должна быть отрицательной в
этой окрестности, а значит и в самой точке, т.е. f (x0 ) 0 (см. рис. 22.6).
+
_
Рис. 22.6
Верно и обратное: если вторая производная отрицательна в точке x0 ,
то она, будучи непрерывной в этой точке, отрицательна в некоторой её окрестности. Значит, существует окрестность точки x0 , где её производная
161

f (x) , переходя через ноль ( f (x0 ) 0 ), меняет знак с плюса на минус. Следовательно, в точке x0 функция f (x) имеет максимум. В тех случаях,
когда вычисление второй производной проще, чем решение неравенства для первой производной, второе условие предпочтительнее.
Пример.Найти экстремумы функции y f (x) x3 3x 1. Функция определена на всей числовой прямой. Её производная
f (x) 3(x2 1) 3(x 1)(x 1)
всюду существует, поэтому абсциссы точек подозрительных на экстремум это те значения переменной, при которых производная равна нулю, т. е. x 1 и x 1. Отметим на следующей схеме знаки производной в соответствующих интервалах
_
Рис. 22.7
Отсюда видно, что в интервале ( , 1) функция возрастает, а в интервале
( 1, 1)– убывает, следовательно, |
при |
x 1 функция имеет максимум |
ymax f ( 1) 3 . Соответственно |
ymin |
f (1) 1. На основе этих данных |
можно построить график этой функции (см. рис. 22.8). «Попутно» мы выяснили, что уравнение x3 3x 1 0 имеет три корня
2 x1 1, |
0 x2 1, |
1 x3 2 . |
162

4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
X: -1 |
|
|
|
|
|
|
|
|
|
|
Y: 3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X: 1 |
|
|
|
|
|
|
|
|
|
|
Y: -1 |
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
-3 |
|
|
|
|
|
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
|
|
|
-2.5 |
-2 |
-1.5 |
-1 |
-0.5 |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
|
|
|
|
|
Рис. 22.8 |
|
|
|
|
|
Лекция 23. Исследование функций и построение их графиков (продолжение)
23.1. Выпуклость. Понятие выпуклости – одно из важнейших понятий всей математики. Мы ограничимся применением этого понятия к исследованию выпуклости графика функции. Обратимся к рисунку.
|
|
Рис. 23.1
163

Пусть в промежутке (a,b) заданы две дифференцируемые функции. Их
графики – это непрерывные кривые, имеющие в каждой точке касательную. Обе функции возрастают в этом промежутке. Но график одной из них обращен «горбом» вниз, а у другой – в противоположную сторону. Это свойство кривой называют выпуклостью. Как описать это свойство в математических терминах?
В математике есть понятие выпуклой функции, применяемое к более широкому классу функций, чем класс дифференцируемых функций. Мы определим это понятие именно для дифференцируемых функций. Будем называть функцию y f (x) выпуклой (вниз) в промежутке (a,b) , если её
график лежит выше касательной в любой точке из этого промежутка (см.
рис. 23.2).
В противном случае функцию называют вогнутой (выпуклой вверх). Аналитически это свойство выразится следующим неравенством
f (x) f (x0 )(x x0 ) f (x0 ) Y (x) ,
правая часть которого представляет собой значение ординаты касательной.
Рис. 23.2 |
|
|
|
Условие выпуклости. Если функция |
y f (x) |
имеет в промежутке |
|
(a,b) положительную вторую производную |
f |
|
, то кривая y f (x) |
(x) 0 |
|||
выпукла (вниз). |
|
|
|
Для обоснования возьмём любую точку |
x (a,b) и рассмотрим |
||
функцию |
|
|
|
R(x) f (x) f (x0 ) f (x0 )(x x0 ) . |
|||
Применим формулу Лагранжа к разности f (x) f (x0 ) |
и получим |
||
164 |
|
|
|

R(x) f ( )(x x0 ) f (x0 )(x x0 ) ( f ( ) f (x0 ))(x x0 ) ,
где точка расположена между точками x и x0 . К разности производных f ( ) f (x0 ) опять применим формулу Лагранжа
|
|
R(x) f ( )( x0 )(x x0 ) , |
|
|
причём точка |
|
находится между точками |
и |
x0 . Покажем, что |
произведение |
( x0 )(x x0 ) положительно независимо от расположения |
|||
точки x по отношению к точке x0 . Пусть сначала точка |
x располагается |
|||
левее точки x0 |
(рис. 23.3). Тогда, очевидно, x0 |
0 и |
x x0 0 . |
|
Рис. 23.3
Если же точка x расположена правее точки x0 (рис. 23.4), то картина будет следующей:
|
|
|
|
|
|
|
|
Рис. 23.4 |
|
|
|
В |
этом |
случае |
x0 |
0 |
и |
x x0 0 . |
Таким |
образом, |
|||
( x0 )(x x0 ) 0 в |
|
любом |
|
случае |
и |
знак |
разности |
||||
R(x) f |
|
|
|
|
|
определяется |
только |
знаком |
второй |
||
|
( )( x0 )(x x0 ) |
||||||||||
производной, откуда и следует доказываемое утверждение. |
|
||||||||||
Например, для функции y arctg x имеем: |
|
|
|||||||||
|
|
|
1 |
|
y |
2x |
|
0, |
x 0 |
|
|
y |
|
|
, |
|
, |
y |
|
|
|
||
|
x2 |
(1 x2 )2 |
|
|
|
||||||
|
1 |
|
|
|
0, |
x 0 |
|
|
|||
Поэтому график этой функции обращён выпуклостью вниз при отрицательных значениях аргумента и выпуклостью вверх при его положительных значениях.
165

2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
-10 |
-8 |
-6 |
-4 |
-2 |
0 |
2 |
4 |
6 |
8 |
10 |
Рис. 23.5
23.2. Точки перегиба.Точки графика функции, в которых направление выпуклости меняется на противоположное, называют точками перегиба. Например, у синусоиды это точки пересечения её графика с осью абсцисс. Необходимым условием существования точки перегиба графика дважды дифференцируемой функции является равенство нулю её второй производной в некоторой точке, а достаточным – перемена знака второй производной при «переходе» через эту точку. Найдем, например, точки перегиба кривой
|
y |
1 |
. |
|
|
|
|
|
|
|
|||
|
1 x2 |
|
|
|||
Для этой функции имеем |
|
|
|
|
|
|
y |
2x |
, y |
3x2 1 |
|||
|
|
|
. |
|||
(1 x2 )2 |
(1 x2 )3 |
|||||
Следовательно, точками перегиба могут быть только точки
P |
|
|
1 |
|
, |
3 |
. |
|
|
|
|
|
|
||||
1,2 |
|
3 |
4 |
|
||||
|
|
|
|
|||||
При переходе через каждую из них вторая производная меняет знак, значит эти точки – точки перегиба (см. рис. 22.2).
При построении графиков полезно вычислить значение первой производной в точке перегиба, дающее направление касательной,
относительно которой происходит |
перегиб. В |
нашем |
примере |
|
y (P |
) 0,65.Кроме того заметим, |
что в точках |
перегиба |
вторая |
1,2 |
|
|
|
|
производная может и не существовать, что видно на графике следующей функции
166

|
|
|
|
1 |
|
|
2 1 |
|
|
||||
y 3 x , |
|
|
|||||||||||
y |
|
|
|
0, y |
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||||
|
|
|
|
33 x2 |
|
|
9 x 3 x2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
0.5 |
|
|
|
|
0 |
|
|
|
|
-0.5 |
|
|
|
|
-1 |
|
|
|
|
-1 |
-0.5 |
0 |
0.5 |
1 |
Рис. 23.6
23.3. Асимптоты. Иногда кривая, имеющая бесконечную ветвь, при удалении её точек в бесконечность «как бы выпрямляется» и приближается к некоторой прямой. Эту прямую называют асимптотой кривой (греч. asymptotos – несливающаяся). Если авторы этого термина подчеркивали то, что кривая не сливается с прямой, то мы обращаем внимание на то, что расстояние точки кривой (x, f (x)) до прямой – асимптоты стремится к
нулю при движении точки вдоль кривой к бесконечности. Пример кривой, имеющей асимптоты, даёт график функции y 1 x
x
Рис. 23.7
Рассмотрим одну из |
ветвей |
этой кривой. Когда точка M (x, y) |
|
стремится к бесконечности, то расстояние её до оси |
Oy , равное d x , |
||
стремится к нулю. Значит |
прямая |
x 0 – вертикальная асимптота. Если |
|
N (x, y) , то d y 0 . Следовательно, прямая |
y 0 –горизонтальная |
||
|
|
167 |
|
асимптота.Как найти вертикальные асимптоты кривой, заданной уравнением y f (x)? Необходимым условием для этого является существование точек разрыва функции. Достаточным условием будет одно из следующих:
lim f (x) ,
x x0 0
где x0 точка разрыва.
Горизонтальные асимптотыкривых, определённых в бесконечном промежутке, определяются существованием конечных пределов:
lim |
f (x) a , |
lim f (x) b . |
|
|
||
x |
x |
|
|
|
||
В этом случае прямые y a |
и |
y b |
– |
горизонтальные |
асимптоты. |
|
Например, график функции |
y arctg x |
при |
x |
имеет асимптоту |
||
y 2 , а при x асимптоту |
y 2 |
(см. рис. 23.5). |
|
|||
Пусть кривая, заданная уравнением |
y f (x) , |
имеет |
наклонную |
|||
асимптоту y k x b . Как найти |
величины |
k и |
b ? Ограничимся |
|||
рассмотрением случая, когда |
x . |
|
|
|
|
|
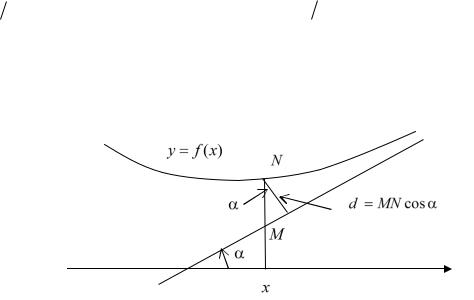
Рис. 23.8
Заметим, что d MN cos , поэтому |
|
d и MN стремятся одновременно к |
|||||||||
нулю при |
x , т.к. const . Значит, |
если кривая |
y f (x) имеет |
||||||||
асимптоту |
y k x b , то |
|
|
|
|
|
|
|
|
|
|
|
lim MN lim f (x) k x b 0 . |
|
(23.1) |
||||||||
|
x |
x |
|
|
|
|
|
|
|
|
|
Преобразуем это выражение к виду |
|
|
|
|
|
|
|
||||
|
|
|
f (x) |
|
b |
0 . |
|
||||
|
|
lim x |
|
|
|
k |
|
|
|
||
|
|
|
x |
|
|
|
|||||
|
|
x |
|
|
|
x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
168
Для того чтобы произведение двух сомножителей, один из которых стремится к бесконечности, стремилось к нулю, необходимо стремление к нулю второго сомножителя, откуда имеем
k lim |
f (x) |
. |
(23.2) |
|
|||
x |
x |
|
|
|
|
|
|
При найденном k из (23.1) |
получим |
|
|
b lim f (x) k x . |
(23.3) |
||
x |
|
|
|
Если при x также существует наклонная асимптота, то ее параметры находятся по аналогичным формулам с заменой x на
x . Если один из пределов не существует или равен |
, то |
соответствующей асимптоты нет. Например, функция y x2 не имеет асимптот. Или другой пример: для функции y x ln x имеем
k lim (1 |
ln x |
) 1 |
, b lim ln x , |
|
|||
x |
x |
x |
|
т.е. у этой кривой нет наклонной асимптоты. Теперь приведем пример кривой, имеющей наклонную асимптоту
|
|
|
|
|
|
|
|
y |
x2 2x 1 |
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для этой функции найдем |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
k lim |
|
x2 |
2x 1 |
1 |
, b lim |
x2 |
2x 1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
x |
2 |
||||||
|
|
x |
2 |
|
|
|
x |
||||||||||
x |
|
|
|
|
|
|
x |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и приведем графики функции и её наклонной асимптоты |
y x 2 |
||||||||||||||||
Используя свойство асимптоты, найдем |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x2 2x 1 |
|
|
(x 2) |
|
x 2016 2018. |
|
|||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
x 2016 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
169
