10216

30

•слой стока y (мм) – количество воды, стекающей с водосбора за какойлибо период, равном толщине слоя, равномерно распределенного по площади этого водосбора (мм в год). y= WF , W (м3 в год), F (м2).

•безразмерная характеристика стока – модульный коэффициент стока Кi,

Все величины зависят от времени, поэтому их применяют с указанием времени: годовые, месячные и т.п.

Величины, средние за несколько лет, называются среднемноголетними

Q0, W0, y0, M0.

Величина средняя за год – среднегодовая.

Средняя величина за такой многолетний период, при увеличении которого эта величина практически не изменяется, называется нормой. Норма стока y , мм – слой воды при условии невытекания, если взять

бассейн реки и считать, что с него ничего не вытекает, а только выпадают осадки [Ресурсы поверхностных вод, Гидрологическая изученность, Водные ресурсы].

Стокообразующие факторы:

•осадки (слой осадков в м),

•испарение (слой испарения с суши и с водной поверхности),

•влажность воздуха,

•рельеф,

•деятельность человека.

Методы определения нормы стока

1. При многолетних гидрометрических наблюдениях.

В этом случае норму стока определяют как среднеарифметическое

продолжительность периода наблюдений за годовым стоком считается достаточной, если ошибка не больше 5-10%.

2. При недостающих гидрометрических данных.

Определяют методом корреляции по графикам связи годового стока в изучаемом бассейне и бассейне-аналоге с многолетними данными по стоку;

31

по приближённой формуле. Сущность этих способов состоит в приведении коротких рядов наблюдений к длительным, путём установления связи между годовым стоком в изучаемом бассейне и стоком в бассейне-аналоге с многолетними наблюдениями.

3. При отсутствии гидрометрических данных.

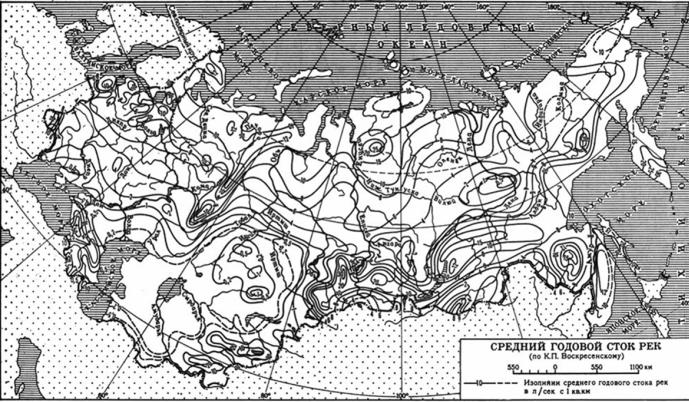
А) Норму сток определяют по карте изолиний среднемноголетнего стока и интерполяцией значений стока между опорными пунктами

которое будет создавать водохранилище.

Этот способ определения стока особенно актуален для малых рек, наблюдения за которыми могут отсутствовать (пр. р. Валава (длина реки 19

км) в г. Лысково. На этой реке создано водохранилище – пруд, который служит для снабжения питьевой водой города).

Б) По эмпирическим формулам.

Η= 9/(d3+9) – ф. Полякова,

Еще есть другие формулы, например, ф. Крицкого и Менкеля.

Выбор расчётного года

Для случаев, когда имеются справочные данные, пользуются [9,10,11].

год – условие необходимое, но недостаточное. Может быть, что численно расчётный год совпадает по средне фиктивному расходу, но распределение стока в течение года иное. Расчётный год помимо того, что должен быть по величине расхода близким к средне фиктивному расходу, также должен быть близким и по характеру гидрографа.

Использование математической статистики в гидрологии

Математическая статистика в основном развивалась в США. Игры, бизнес всегда просчитывались, т.е. вычислялась вероятность. Все эти

33

лотереи, лотто-миллионы … бизнесмен никогда себе в убыток не создаст никакую лотерею.

Методы математической статистики, основанные на теории вероятности, имеют широкое применение при исследовании гидрологических явлений и, в особенности, при расчетах стока.

Основная задача расчетов стока заключается в получении данных, характеризующих сток в будущем, когда будут действовать проектируемые мероприятия

Случайные величины и закон их распределения

Случайная величина заранее неизвестна, расходы воды являются такими величинами, но в то же время, эти величины являются дискретными, т.е. в каждый момент времени они приобретают чётко определённое значение. На рисунке можно это изобразить в виде ломанной линии, которая не поддаётся никакой закономерности (мы привыкли к линейной зависимости, параболе, здесь все величины случайные). Я могу поставить точку, когда событие произошло, зависимость этой ломанной находится за пределами наших экспериментальных знаний. Начнём обрабатывать эти случайные величины.

За эти 15 лет расходы представились в такой хаотичной зависимости, что к точному значению мы не придём, но мы можем назвать максимальный и минимальный расходы. Составим вспомогательную таблицу, где расходы представляются в убывающем порядке.

34

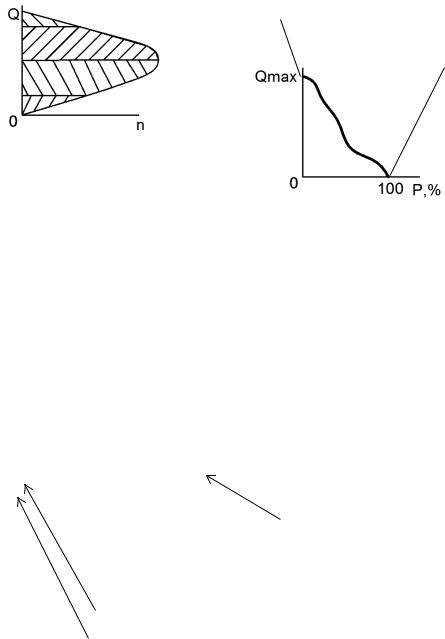
На основании данных строятся два графика: 1) кривая повторяемости - она является кривой распределения расходов воды и 2) кумулятивная кривая, в гидрологии получила название эмпирическая кривая ежегодных вероятностей превышения расходов воды – кривая обеспеченности.

По Волге имеется ряд наблюдений ≈115 лет с 1814 г. Было подмечено, что имеются циклы: 11-летние, когда половодье было поменьше, 22-летние, половодье побольше, в них были критические значения, которые повторялись в определенные годы. Расходы, которые чаще всего повторяются, наиболее вероятны и не будут 100 процентно известны.

Свойства кривой распределения

График кривой повторяемости повернём на 90о.

Расходы Q обозначают через X, число случаев – через У. Самое большое число случаев соответствует какому-то расходу Q, но наблюдения могут проводиться не только над Q, но и над другой величиной (слой, объём стока и др.), поэтому обычно Х – относительная величина.

определяющих норму стока.

Гидрологические явления обычно характеризуются асимметричным распределением. Распределение годового, максимального, минимального и других характеристик стока имеют положительную асимметрию – мода и медиана лежат левее центральной ординаты.

Типы гистограмм (кривых распределения), которые соответствуют рекам

1) Кривая Гаусса (симметричная кривая). Таких рек не бывает, это просто идеал. Она не выражается никакой математической формулой.

2)Малые реки – умеренная асимметричность. Большие расходы чаще повторяются, чем меньшие.

3)Асимметричная гистограмма. Малые расходы встречаются очень часто, большие расходы – редко. Это реки Кавказа

4)U –образная гистограмма. Расходы или очень большие или очень маленькие. Это реки пустынь, где они пересыхают.

Характеристики гистограмм (кривых распределения)

Характеристики описывают закон распределения: 1. Амплитуда

А=Xmax - Xmin

Если А – велико, прогноз сделать сложно. Х-норма, Хi-текущее значение.

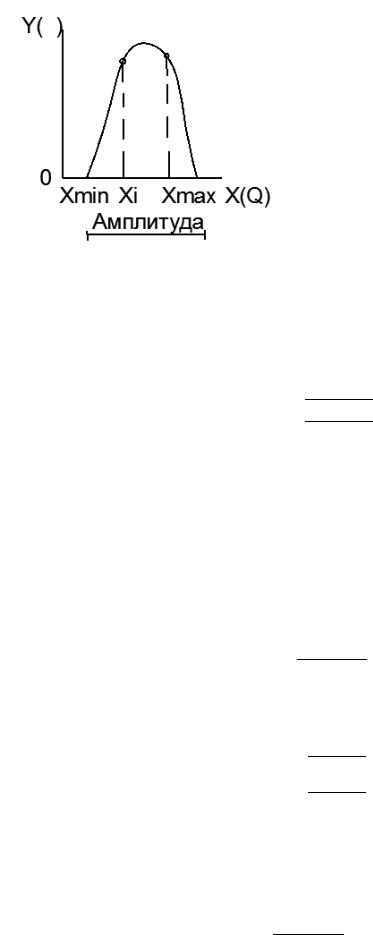
36

прогноз. В гидрологии (n-1), вместо n - в математике, т.к. считается, что в природе нельзя предугадать событие со 100% вероятностью.

4. Дисперсия Показывает, как рассеиваются наблюденные точки: Если дисперсия

малаХ, то это сглаженная кривая, если большая, то и рассеивание большое.

К = Х - модульный коэффициент.

2 = ∑1( − ) n−1 .

5. Коэффициент вариации.

Характеризует отклонение любого члена ряда от середины.

Если реки имеют низкое изменение Q, то Сv мал.

= ∑( −−11)2.

37

2

Это уравнение послужило отправной точкой для дальнейших исследований и его интегрирования. Мы имеем 100 лет наблюдений: самый большой расход будет вероятен 1%, а самый маленький – 100% (т.к. если будет высокий расход, то малый точно будет). Чтобы оценить вероятность, надо расходы просуммировать, а значит, уравнение Пирсона

X – расходы. В 1938 г. это уравнение уточнил наш ученый Рыбкин. Перейдем от рис 1 к рис 2.

38

Расчетные расходы (max и min)

Чаще всего не встречаются

По уравнению Фостера составлены таблицы, которые дают значения ординат кривой обеспеченности. Нормативные отклонения от середины значений ординат биномиальной кривой обеспеченности (бином с 2-мя хвостами) - точное название этих таблиц.

По значениям этой таблицы строится график. Определим линию среднего года (по 50%)

39

Kp% = Фp% * Сv + 1

Фp% - вероятная прибавка

Qp%= Kp% * Q

Все сооружения рассчитаны на такой расход, который может случиться

1 раз в 10 000 лет. Кстати, мифы разных религий повторяются (христ., буддизм), но и они говорят о событиях, произошедших 9 000 лет назад. Монахи Киево-Печерской лавры составляли летописи. По этим летописям были составлены гидрологические отчеты для Днепра за 800 лет. Самое большое половодье укладывалось в интервал 300 лет – катастрофические события, которые подсчитали.

Цель гидрологических расчетов состоит в построении кривой обеспеченности для своего ряда наблюдений.

Формально кривая обеспеченности может уйти в область

положение нереально, нет отрицательных расходов. Поэтому метод расчета,

правдоподобия, для этого необходимо найти две статистические характеристики: