9612

задается в виде упорядоченной пары (vi ,vj ), где vi есть начальная вершина дуги, а vj есть ее конечная вершина. Во втором случае каждое ребро из множества E задается в виде пары (vi ,vj ), в которой (i j). Для

ориентированных (нериентированных) мультиграфов каждая дуга

(ребро) из множества E задается в виде тройки ((vi ,vj n) ,i j ), где nномер дуги (ребра) соединяющей (соединяющего) вершины vi и vj . Например, графы а, б на рис. 64.1 могут быть описаны следующим образом:

задается в виде тройки (vi , v j , r) ( (vi ,v j , r) , (i j ), где число r означает пропускную способность дуги (ребра). Например, ребро, соединяющее вершины v1 и v2 . в графе на рис. 62.2,г будет описано так:

(v1 ,v2 ,48) .

64.2. Основные понятия в теории графов. В дальнейшем под записью G V , E будем понимать неориентированный граф или мультиграф, оговариваяпри необходимости, какой именно граф имеется в виду. Пусть V v1 ,v2 ,..., vn есть множество вершин графа. Две вершины vi и

vj называются смежными, если ребро (vi ,vj )принадлежит E. Ребро (vi ,vj ) называется инцидентным вершинамvi и vj , а вершины vi и vj , называются инцидентными ребру (vi ,vj ). Если ребро является петлей, то оно

считается дважды инцидентной соответствующей вершине.

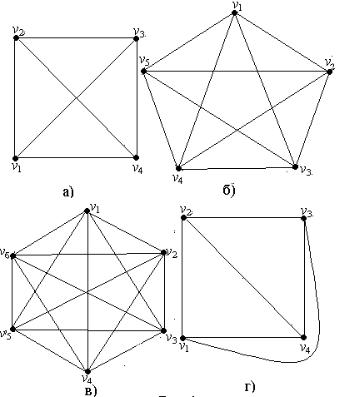
Граф без петель, в котором все вершины смежные, называется полным. На рис. 64.4,а- 64.4,в приведены полные графы с четырьмя, пятью и шестью вершинами.

64.2,а и рис. 64.2,в имеем:

а) d (v1 ) =5, d (v2 ) =6, d (v3 ) =3, d (v4 ) =3, d (v5 )=3 , в) d (v1 ) =3, d (v2 ) =4, d (v3 ) =3, d (v4 ) =3, d (v5 )=3 ,

Так как каждое ребро инцидентно двум вершинам, то:

сумма степеней всех вершин графа является четным числом

иравно удвоенному числу ребер;

в любом графе число вершин с нечетными степенями является четным.

Всправедливости этих утверждений легко убедиться, просмотрев граф, изображенный на рис. 64.2,а. Рёбер в этом графе 10, сумма степеней равна 20 и в нем 4 вершины с нечетными степенями.В полном графе с

nвершинами степень каждой вершины равна (n-1), а т.к. каждое ребро соединяет две вершины, то:

в полном графе с nвершинами содержится n(n-1)/2 ребер.

Граф G V , E называется подграфомграфа G V , E ,если V1 V и E1 E , т.е. если каждая вершина графа G1 является вершиной графа G и

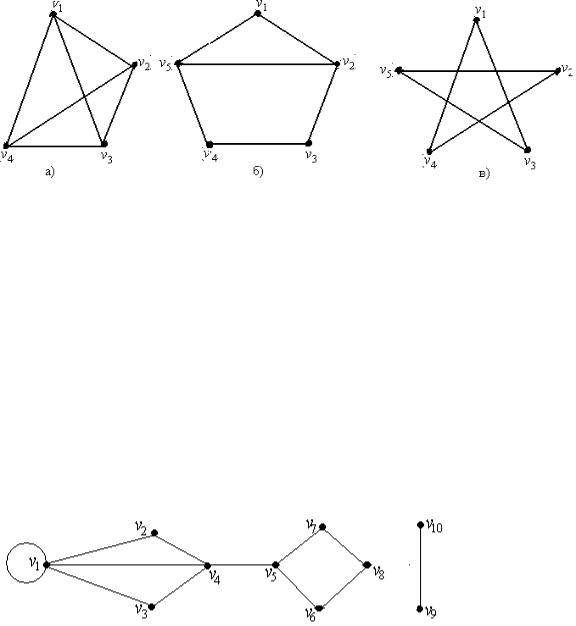
ребро графа G V , E с вершинамииз множества V1 , является также ребром и в графеG1 ´ V1, E1 .

Рис. 64.5

Графы на рис. 64.5 являются подграфами графа, изображенного на рис. 64.4,б, но только подграф на рис. 64.5,аявляется порожденным множеством вершин v1 ,v2 ,v3 ,v4 .

Пусть задан граф G V , E с множеством его вершин V v1 ,v2 ,..., vn . Путь длины nв данном графе это последовательность вершин

Lvi1 ,vi2 ,vi3 ,..., vik ,vik 1 ,..., vin ,vin 1 ,

вкоторой вершины vik и vik 1 (k=1,…,n) соединены ребром. Вершина vik

называется началом пути L , а вершина vik 1 называется концом пути L . В

по какому

Две вершины графа связными, если

существует путь L , их соединяющий. Граф называется связным, если любые две его вершины могут быть соединены путем. Существует расхожее высказывание, что упомянутый выше «граф знакомств», в котором в качестве вершин выступают люди всей земли, является связным, и более того, что любые две вершины в нем могут быть соединены путем, длина которого, не превосходит шести.

В графе на рис.64.6 вершины v1 и v10 связными не являются, т.к.

отсутствует путь, их соединяющий, и потому граф, изображенный на этом рисунке, связным не является.

Если граф G несвязен, то множество его вершин V можно разбить на несколько подмножеств V1 ,V2 ,....,Vk , в каждом из которых вершины связаны

между собой. Подграф, порожденный каждым таким подмножеством, называется компонентой связности графа G и, таким образом, считается, что граф Gсостоит из k компонент связности. Граф G на рис. 64.6 состоит из 2-х компонент связности. Первая компонента определяется подмножеством вершин v1 ,v2 ,..., v8 , а вторая компонента определяется

подмножеством вершин v9 ,v10 .

Ребро, после удаления которого компонента связности графа перестает быть связной, называется мостом. В графе на рис. 64.6 ребро(v4 ,v5 ) является мостом.

Внеориентированном графе:

путь, в котором нет повторяющихся ребер называется цепью;

цепь без повторяющихся вершин называется простой;

цепь, в которой совпадают концевые вершины, называется циклом;

цикл, в котором нет повторяющихся вершин, кроме концевых, на-

зывается простым циклом, или контуром.

В графе G, представленном на рис. 64.6 путь L1 v1 ,v2 ,v4 ,v3 соединяет

потому что вершинаv1 появляется дважды.

64.3. Эйлеровы графы. Пусть G V , E есть неориентированный

граф. Цепь, содержащая все ребра графа, нзывается эйлеровой цепью. Цикл, содержащий все ребра графа, называется эйлеровым циклом.Цикл

После введенных определений вопрос Иммануила Канта относительно кенигсбергских мостов может быть сформулирован так: существует ли эйлеров цикл в графе нарис. 64.3,б?

Теорема (Эйлер). Связный граф содержит эйлеров цикл (и

называется эйлеровым)тогда и только тогда, когда степени всех его вершин являются четными числами. Связный граф, у которого степени только двух

вершин являются нечетными числами, содержитэйлерову цепь (и называется полуэйлеровым).

Так как в графе кенингсбергских мостов (рис. 64.3,б) все вершины имеют нечетные степени, то из данной теоремы следует отрицательный ответ на вопрос Иммануила Канта. Более того, эйлерова цепь в нем также

отсутствует, т.к. он имеет 4 вершины с нечетными степенями. Граф на рис. 64.7 с учетом пунктирного ребра содержит эйлеров цикл, а без учета пунктирного ребра содержит эйлерову цепь.

Рис. 64.7

Если граф является эйлеровым, то алгоритм нахождения эйлерова цикла состоит в следующем: выйдя из произвольной вершины, последовательно зачеркиваем проходимые ребра, остерегаясь пройти по мосту при наличии другой возможности. Если граф является полуэйлеровым, то для нахождения эйлерова пути, необходимо: 1) соединить дополнительным ребром две вершины с нечетными степенями; 2) в полученном эйлеровом графе найти эйлеров цикл; 3) в найденном эйлеровом цикле удалить дополнительное ребро.

Рассмотрим граф на рис. 64.7. После введения пунктирного ребра (v1,v5) граф становится эйлеровым. Начнем поиск эйлерова цикла с 1-ой вершины. На рис. 64.8 указана одна из возможных последовательностей прохождения его ребер. Искомый эйлеров цикл будет таким:

v1,v1,v2,v4,v3,v1,v5,v7,v8,v6,v5,v4,v1.

Заметим, что после 6-ого шага нельзя из вершины v5,идти в вершину v4, т.к. ребро (v4,v5) послеудаления пройденных ребер стало мостом. Вычеркнув из полученного цикла ребро (v1,v5) и переставив начальный его кусок в конец, получаем искомую эйлерову цепь

v5,v7,v8,v6,v5,v4,v1,v1,v2,v4,v3,v1.

между вершинами. При взгляде на рис. 64.8 обращает на себя внимание тот факт, что, если поменять местами наименования вершин, стоящих на правой вертикали графа на рис. 64.8,б (верхнюю вершину назвать v4, анижнюювершину назвать v2), то алгебраическое описание этого графа будет совпадать с алгебраическим описанием графа на рис. 64.8,а.

Этот пример показывает, что нередко два графа с одинаковым количественным составом вершин и ребер отличаются друг от друга просто

нумерацией вершин. В связи с этим, в теории графов вводится очень важное понятие изоморфизма графов.

Два графа G1 V1, E1 и G2 V2 , E2 называются изоморфными, если между элементами множеств V1 иV2 можно установить взаимно однозначное

соответствие f , при котором пара (vi,vj) E1, тогда и только тогда, когда (f (vi), f(vj)) E2 , т.е. вершины vi и vj соединены ребром в графе G1только в

том случае, когда вершины f (vi) и f(vj) соединены ребром в графе G1. Иначе говоря, соответствие fсохраняет свойство пар вершин быть смежными.

Если два графа, представляющие собой математические модели различных изучаемых явлений, оказываются изоморфными, то, повидимому, эти явления обладают общими объективными закономерностями.

Рис. 64.8

Непосредственно из определения следует, что все вершинно-реберные свойства изоморфных графов идентичны. Потому, если найдется свойство такого типа, которым обладает один граф и не обладает другой, то такие два графа являются неизоморфными. Так, сразу видно, что графы 64.8,в и 64.8,г на рис. 64.8 неизоморфны, т.к. в графе 64.8,в степени 4-х вершин равны 3, а в графе 64.8,г только две вершины имеют степени, равные 3. У графов 64.8,г и 64.8,д на этом рисунке наборы степеней всех вершин совпадают (у двух вершин степени равны 3 и у 4-х вершин степени равны). Однако эти графы также неизоморфны, ибо в графе на рис. 64.8,г имеется цикл длины 3, а в графе на рис.64.8,д такого цикла нет.

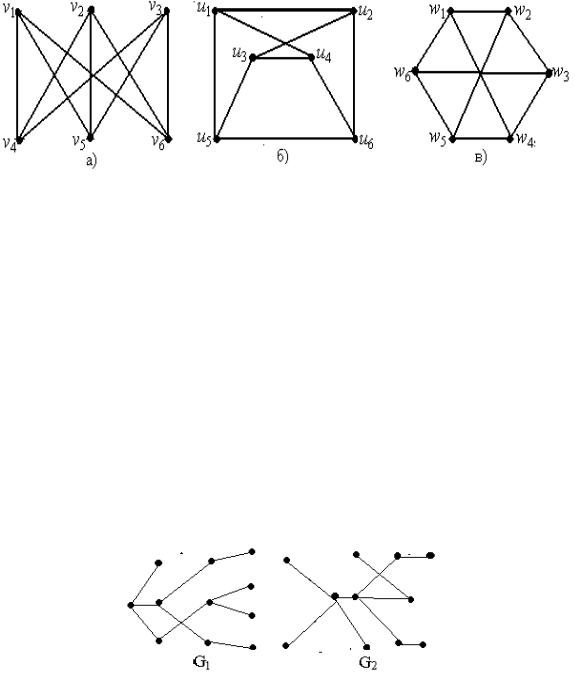
Рис. 64.9

В общем случае вопрос о том, являются ли два графа с одинаковым количеством вершин изоморфными или нет, представляет очень сложную комбинаторную задачу. Нижеследующий пример показывает, что даже по изображению на рисунках не так просто выяснить, являются ли графы изоморфными или нет. С первого взгляда далеко не очевидно, что графы 64.9,а, 64.9,б, 64.9,в на рис. 64.9 изоморфны между собой. Но следующие соответствия между вершинами графов убеждают нас в этом:

v1 u1 w1, v2 u3 w3, v3 u6 w5, v4 u5 w2, v5 u2 w4, v6 u4 w6

64.5. Деревья. Очень важным в теории графов является понятие дерева. Деревом называется связный граф, не содержащий циклов. Графы G1 и G2 на рис. 64.10 являются деревьями, а графыG3(есть цикл) иG4(не является связным) деревьями не являются.

Рис. 64.10,а

Дерево обладает следующими свойствами:

каждое дерево, состоящее из n вершин, содержит ровно (n-1) ребро;

любые две вершины дерева соединены ровно одной простой цепью;

каждое ребро дерева является мостом.

Рис.64.10,б

В приведенных на рис. 64.10,а изображениях деревьевG1иG2имеются пересекающиеся ребра, но эти графы можно нарисовать так, чтобы никакая пара ребер не пересекалась.

Остовом связного графа G V , E называется подграф,

содержащий все его вершины и являющийся деревом.

Рис. 64.11

Деревья, изображенные на рис. 64.11,б и рис. 64.11,в представляют собой два различных остова графа, изображенного на рис.64.11,а

Рис. 64.12,а

На графе на рис. 64.12,а изображены населенные пункты. В одном из них необходимо установить электростанцию, от которой будут протянуты провода во все остальные пункты. «Веса» на ребрах графа 64.12,аобозначают стоимость (в тысячах рублей) прокладки проводов между соответствующими пунктами. Строящаяся электросеть будет представлять собой остов графа 64.12,а, ибо она должна охватывать все пункты и не должна содержать циклов.

Граф, изображенный на рис. 64.12,б является примером такой электросети, а сумма весов на ребрах этого дерева, равная 268 тыс. руб., означает стоимость реализации электросети, согласно данному проекту. Естественно возникает вопрос: существует ли проект электросети более дешевый?

Рис. 64.12,б

Если отвлечься от конкретной данной ситуации, то этот вопрос можно сформулировать в виде следующей задачи. Для взвешенного связного графа найти остов, сумма весов ребер которого была бы минимальна.

Приведем без доказательства алгоритм Прима, решающий данную задачу. Пусть дан взвешенный граф G V , E , имеющий n вершин.

Алгоритм Прима состоит в следующем. На первом шаге выбираем в графе G´ребро минимального веса. Оно представляет собой деревоD1 , состоящее из одного ребра. Далеесреди ребер, соединяющих вершины дереваD1 с вершинами графа G´, которые не входят в D1, выбираем ребро минимального веса и присоединяем его к дереву D1 . Получается дерево D2

, состоящее из двух ребер. Далеесреди ребер, соединяющих вершины дерева D2 с вершинами графа G´, которые не входят в D2 ,выбираем ребро

минимального веса и присоединяем его к дереву D2 . Получается дерево D3 , состоящее из трех ребер.

Дерево Dn 1 , построенное в результате повторения описанной

процедуры (n-1) раз, будет являться остовом минимального веса.

Применяя алгоритм Прима к приведенному выше примеру, получим проект реализации требуемой электросети, приведенный на рис.64.13. Выбор ребер при построении данного проекта проходил в следующей последовательности:

(v3,v6), (v3,v10), (v3,v1), (v10,v8), (v8,v11),(v6,v4), (v4,v5), (v5,v9), (v1,v2),

Рис. 64.13

Нетрудно посчитать, что стоимость реализации электросети по данному проекту составляет 157 тыс. руб. Отметим, что стоимость затрат по данному проекту не зависит от того, где будет установлен источник электроэнергии, но, быть может, лучше его установить в вершине v3.