Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

9522

.pdf

Скачиваний:

Добавлен:

25.11.2023

Размер:

2.81 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 105 6 7 8 9 10 > Следующая >>>

x (t) dt F(x) F( ) F(x) .

Что и требовалось доказать.

Итак, для полной характеристики случайной величины достаточно знать или функцию распределения, или плотность распределения вероятностей (т.к. одну из них можно выразить через другую):

F(x) x (t) dt	или (x) F'(x) .

Рис. 6.4. Иллюстрация свойства 4 функции плотности распределения

______________

Пример. Найти функцию распределения случайной величины, плотность вероятности которой:

(x)	1	.

	(1 x2 )

Решение. По только что доказанному свойству:

				F(x) x (t) dt x		1				dt
				F(x) x (t) dt x	(1 t			2	)	dt
					(1 t				)

1	arctg t	x	1	( arctg x arctg ( ) )		1	( arctg				x	)	1	1	arctg x .
1			1			1							1	1

												2	2

Лекция № 7

Примеры распределения непрерывных случайных величин

1. Равномерное распределение

Определение. Случайная величина с плотностью вероятности

0	при x a и	x b	, где C const,
(x)			, где C const,
C	при a x b

называется равномерно распределённой величиной.

Равномерный закон распределения используется: при анализе ошибок измерения, когда проводятся численные расчёты; в ряде задач массового обслуживания.

Найдём величину C из условия

(x) dx 1 (свойство 3o плотности вероятно-

сти):

(x) dx

0 dx

C dx

0 dx C

dx C x

b C(b a)

дол жно

быть

Поэтому С

а плотность вероятности равномерно распределённой величины

b a

имеет вид:

при x a и

x b

(x)

при a x b

b a

Найдём также функцию распределения равномерно распределённой величи-

ны. По свойству 4o

для плотности вероятности:

0 dt

при x a

F (x)

(t) dt

0 dt

b a

при a x b

0 dt

b a dt 0 dt

при b x



0
x	1
	1

		dt
	b a	dt
a
b	1
	1

b a dt
a

при x a

при a x

при b x

b 1b a1b a

(x a)

(b a)

при x a		0	при x a

	x a		при a x b .
при a x b
при a x b
	b a
		1	при b x
при b x
при b x

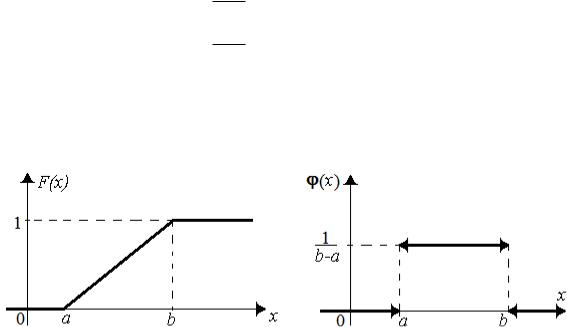
Графики функций F(x) и (x) приведены ниже на рис. 7.1. На графике для функции (x) четыре стрелки означают, что левый или правый пределы не достижимы функцией в соответствующей точке.

Рис. 7.1. Равномерное распределение

Пример. Поезда метрополитена идут регулярно с интервалом 2 минуты. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придётся не более полминуты.

Решение. Пусть случайная величина X - время ожидания пассажира. Тогда её плотность вероятности равна:

0		при x 0 и	x 2
			.
(x)	1	при 0 x 2	.


2

Поэтому по свойству 1o для плотности вероятности получим:

		1				1

P(0 X	1	) 2	1	dx	1	2 dx	1	x	10/ 2	1	.
	1		1		1		1			1
	2		2		2		2			4

		0				0
		0				0

2. Нормальное распределение

Определение. Случайная величина имеет нормальный закон распределения

(закон Гаусса), если её плотность распределения вероятностей имеет вид:

(x)	1		( x a)2	,
(x)			2 2	,
		e	2 2
	2	e

где a и - параметры распределения ( 0, a ).

Нормальный закон распределения наиболее часто встречается на практике. Главная его особенность – он является предельным законом, к которому приближаются другие законы распределения (при типичных условиях).

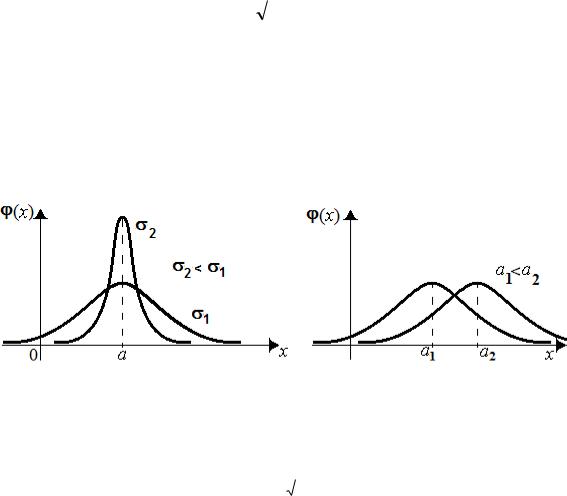
Плотность вероятности (x) - функция, похожая на колокол. Зависимость от параметров такова (рис. 7.2). При уменьшении только параметра , график функции вытягивается и поднимается вверх по оси ординат. А при увеличении только параметра a , график симметрично передвигается вправо вдоль оси абсцисс:

Рис. 7.2. Функция плотности распределения нормальной величины

Функция распределения F(x) нормального распределения

x	1	x	(t a)2
F(x) (t) dt		e	2	2	dt


	2

имеет вид, изображенный на рис. 7.3:

Рис. 7.3. Функция распределения нормальной величины

а) Правило «трёх сигм»

Найдём вероятность того, что изучаемая случайная величина (распределённая нормально) примет значение в пределах от до :

	1		( x a)2
P( X ) (x) dx		e	2	2	dx .



	2

Для этого воспользуемся известным из математического анализа свойством определённого интеграла:

b	f (x) dx c	f (x) dx b	f (x) dx
a	a	c

и, используя ещё одно свойство:

f (x) dx a

f (x) dx ,

окончательно получим:

f (x) dx b

f (x) dx a

f (x) dx .

Этим равенством и воспользуемся (при условии,

что роль c

играет параметр a из

нормального закона)

( x a)2

P( X )

2 2

dx .

2 a

Далее сделаем замену t

x a

в определённых интегралах (тогда dt d (

x a

)

или

dx dt ):

( x a)2

P( X )

2 2

2 a

t 2

2 dt

2 a a

		a										a
	1		e	t 2			1						e	t 2		a ) (		a ) ,
	1			2	dt		1							2	dt (
				2										2

	2	0							2		0
						1		x		z 2
где функция Лапласа			(x)			1		e		2 dz			затабулирована				и приводится в приложе-


						2 0

нии 2 из [2]. В частном случае, когда интервал симметричен относительно точки a , эта формула выглядит так:

P(a X a ) (	a a	) (	a a	) (	) (	) 2 (	)

или так:

P( X a ) 2 ( ) .

Отсюда правило «трёх сигм» выводится следующим образом. Рассмотрим вероятность того, что изучаемая случайная величина (распределённая нормально) примет значение в пределах от a 3 до a 3 :

P(a 3 X a 3 ) 2 (3 / ) 2 (3) .

Из таблицы для функции Лапласа находим, что (x) 0,49865, поэтому

P(a 3 X a 3 ) 2 0,49865 0,9973,

т.е. вероятность встретить значение изучаемой случайной величины именно на интервале [a 3 , a 3 ] велика - 0,9973!!!

3. Показательный (экспоненциальный) закон распределения

Определение. Случайная величина X имеет показательный (экспоненциаль-

ный) закон распределения, если её плотность распределения вероятностей имеет вид:

0	при x 0	,
(x)		,
e x	при x 0

где параметр распределения ( 0 ).

Он возникает в теории массового обслуживания, теории надёжности. Например, интервал времени T между двумя соседними событиями (заявками) в потоке поступающих заявок на обслуживание (ремонт телевизоров, автомобилей, …) имеет показательный закон распределения (с интенсивностью ).

Примерный график плотности распределения вероятностей (x) приводится на рис. 7.4.

Рис. 7.4. Функция плотности распределения показательной величины

Отсюда, функция (x)

Определим вид функции распределения для показательного закона:

0 d t 0

при x 0

F(x) (t) dt x

d t

0 d t e

d t e

d ( t)

при x 0

e x

при x 0

Примерный график функции распределения F(x) приводится на рис.7.5.

Рис. 7.5. Функция распределения показательной величины

4. Логарифмически-нормальное распределение
Определение. Случайная величина							X (X 0)			имеет логарифмически-
нормальное (логнормальное) распределение, если её натуральный логарифм
ln X подчинён нормальному закону:
0				при	x 0
				ln x		(t a)2
F(x) P(ln X ln x)	1
F(x) P(ln X ln x)	1			e		2		2	d t	при x 0 .


		2
		2	0

плотность распределения вероятностей логнормального распределения имеет вид (по правилу дифференцирования интеграла, зависящего от параметра)

0	1	при		x 0
(x)	1				2
				(ln x a)2
			e	2		при x 0 .


	2 x
	2 x

Примерный вид графика функции (x) приведён на рис. 7.6.

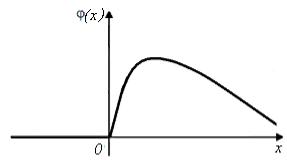
Рис. 7.6. Функция плотности распределения логнормальной величины

Логнормальное распределение встречается при описании распределения доходов, банковских вкладов, долговечности изделий в режиме износа – старения, месячной зарплаты, посевных площадей под различные культуры и т.п.

5.Вейбуловское распределение

Винженерной практике часто используется распределение ВейбуллаГнеденко:

0	при x 0
		,
F (х)	e ( x / )	,
1	e ( x / )	при x 0

0	при x 0

(x)	1		( x / )
	1	e	( x / )	при x 0
( / ) x /		e		при x 0

с параметрами 0 и 0 . Данное распределение часто используется для описания распределения экстремальных значений системы случайных величин:

X max (n) max( X1, X 2 ,...X n ) , X min (n) min( X1, X 2 ,...X n ) ,

кроме того оно используется для описания времени и интенсивности отказов в теории надежности сложных систем.

Частными случаями распределения Вейбулла-Гнеденко являются следующие распределения :

-Показательное распределение 1/ 0 , 1,

-Релеевское распределение 0 , 2 .

Лекция № 8

Числовые характеристики случайных величин

1. Математическое ожидание. Дискретные случайные величины

Пусть задана случайная величина X своим рядом распределений

	Значения случайной величины ( X )	x1	x2	x3	xn

	Вероятности значений ( P )	p1	p2	p3	p n
	Определение. Математическим ожиданием дискретной случайной величи-
ны X называется сумма произведений всех возможных значений xi					случайной вели-
чины на вероятности pi этих значений:

n( )

xi pi M[X ] M (X ) mX .

i 1

Примечания. 1. Все три приведённые обозначения математического ожидания равноправны.

2.Верхний индекс у знака суммы ( n или ) соответствует тому, что X принимает конечное число значений ( n ) или бесконечное число значений.

3.Сумма всех участвующих (в определении) вероятностей равна единице (попробуйте это доказать):

n( )
pi	1.

i 1

______________

Пример. Два стрелка стреляют по мишени. Число очков, которые выбивает каждый стрелок, заданы следующими законами распределений:

X1	1		2		3		4		5
P( X1 xk )	0		0		0,3		0,4		0,3


X 2		1		2		3		4		5
P( X 2 xk )		0,1		0,1		0,1		0,2		0,5

Какой из стрелков опытнее, кого нужно взять на соревнование (между вузами), кому нужно отдать предпочтение?

Решение. Задача па первый взгляд непростая. Но если воспользоваться понятием математического ожидания (найти среднее число очков, выбиваемых каждым стрелком при одном выстреле), задача переходит в разряд решаемых.

Действительно, для первого стрелка математическое ожидание равно:

M (X1) 1 0 2 0 3 0,3 4 0,4 5 0,3 0,9 1,6 1,5 4,0 ,

(т.е. он выбивает в среднем 4,0 очка за один выстрел), а для второго стрелка

M (X 2 ) 1 0,1 2 0,1 3 0,1 4 0,2 5 0,5 0,1 0,2 0,3 0,8 2,5 3,9 .

То есть пока опытнее (точнее) первый стрелок. Но если второй «уберёт» шлейф плохих выстрелов, то он станет вне конкуренции!

Свойства математического ожидания

Свойство 1o . Математическое ожидание постоянной величины равно этой постоянной:

X C const M (X ) M (C) C

Доказательство. Действительно, пусть случайная величина X равна C const с вероятность p 1. Тогда по определению математического ожидания:

M(X ) C 1 C .

Что и требовалось доказать.

Свойство 2o . Постоянный множитель можно выносить за знак математического ожидания:

M (k X ) k M (X ) , где k const.

Доказательство. Докажем это для случайной величины X , которая принимает конечное число n значений xi ,i 1, , n . По определению математического ожи-

дания:

M (k X ) k xi pi .

i 1

Отсюда, вынося константу за знак суммы, получим:

n	n
k xi pi	k xi pi k M (X ) .
i 1	i 1

Что и требовалось доказать.

Свойство 3o . Математическое ожидание суммы конечного числа случайных величин равно сумме математических ожиданий этих величин:

M ( X1 X 2 X k ) M ( X1) M ( X 2 ) M ( X k ) .

Доказательство. Докажем это для математического ожидания величины, составленной из суммы двух случайных величин X и Y , причем случайная величина X , принимает конечное число n значений xi ,i 1, , n , а случайная величина Y , при-

нимает конечное число m значений y j , j 1, , m . Тогда математическое ожидание суммы двух величин X и Y равно:

	n		m
	M (X Y) (xi y j )P( X xi ,Y y j )
	i 1		j 1
n	m		n	m
xi P( X xi ,Y y j ) y j P( X xi ,Y y j ) .
i 1	j 1		i 1	j 1
Попробуем разобраться с первой двойной суммой
	n		m
	xi P( X xi ,Y y j ) .
	i 1	j 1
В ней от значения xi не зависит внутренняя сумма, поэтому вынесем					xi за знак этой
суммы:
n	m		n	m
xi P( X xi ,Y y j ) xi P( X xi ,Y y j ) .
i 1	j 1		i 1	j 1
Событие, состоящее в том, что X			примет значение xi (вероятность этого события
равна P( X xi ) ), влечёт за собой событие, которое состоит в том, что					X Y примет
значения:

X xi ,Y y1 или X xi ,Y y2 , , или X xi ,Y ym ,

а вероятности этих несовместных событий равны соответственно:

P( X xi ,Y y1) или P( X xi ,Y y2 ), , или			P( X xi ,Y ym ) .
Тогда вероятность P( X xi )		первоначального события	X xi равна (по теореме о
сложении вероятностей несовместных событий):
		m
	P( X xi ) P( X xi ,Y y j ) .
		j 1
Поэтому первая двойная сумма равна:
n	m	n
xi	P( X xi ,Y y j ) xi P( X xi ) M ( X ) .
i 1	j 1	i 1

Последнее же равенство следует из определения математического ожидания.

Со второй двойной суммой поступим аналогично, но прежде заметим, что она не изменится, если поменять порядок суммирования:

n	m	m	n
y j P( X xi ,Y y j ) y j P( X xi ,Y y j )
i 1	j 1	j 1	i 1

(Это известное свойство можно проверить,				расписав его для случаев i 2, j 2 или
i 3, j 2 ). А далее:
m	n	m	n		m
y j P( X xi ,Y y j ) y j P( X xi ,Y y j ) y j P(Y y j ) M (Y ) .
j 1	i 1	j 1	i 1		j 1
Поэтому окончательно получаем:
	n	m		n	m
	M(X Y) xi P( X xi ,Y y j ) y j P( X xi ,Y y j )
	i 1	j 1		i 1	j 1

M (X ) M (Y) .

Что и требовалось доказать.

Свойство 4o . Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:

M (XY) M (X ) M (Y).

Без доказательства (для заинтересовавшихся студентов это доказательство – повод повысить итоговую оценку).

______________

Пример. Вероятность попадания в мишень при одном выстреле равна p 0,2 . Найти число независимых выстрелов, обеспечивающее математическое ожидание равное 5 попаданиям в мишень (например, при стрельбе по кораблю).

Решение. Пусть случайные величины			X1, X 2 , , X n - есть число попаданий в
мишень при каждом из n выстрелов. Тогда, согласно условию задачи, все эти слу-
чайные величины Xi ,i 1,2, , n, имеют один и тот же закон распределения

	X i	0		1

	P	0,8		0,2
	P
Математическое ожидание этих случайных величин равно:

M ( Xi ) 0 0,8 1 0,2 0,2.

Математическое ожидание числа попаданий в мишень при n выстрелах равно M ( X1 X 2 X n ) . По свойству 3o (математического ожидания):

M ( X1 X 2 X n ) M ( X1) M ( X 2 ) M ( X n ) n M ( Xi ) n 0,2 5 ,

<<< < Предыдущая 1 2 3 45 / 105 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.11.20232.8 Mб09518.pdf
#
25.11.20232.8 Mб09519.pdf
#
21.11.2023164.37 Кб0952.pdf
#
25.11.20232.81 Mб49520.pdf
#
25.11.20232.81 Mб09521.pdf
#
25.11.20232.81 Mб09522.pdf
#
25.11.20232.81 Mб09523.pdf
#
25.11.20232.81 Mб09524.pdf
#
25.11.20232.81 Mб69525.pdf
#
25.11.20232.81 Mб09526.pdf
#
25.11.20232.82 Mб09527.pdf