
9435
.pdf11
Структура и объём работы. Диссертационная работа состоит из введения, шести глав, заключения, списка литературы и пяти приложений. Основной текст содержит 435 страниц. Список литературы состоит из
431 наименования. Приложения выполнены на 60 страницах.
Личный вклад автора. Все теоретические и практические результаты работы, изложенные в диссертации, получены лично автором. Конфликт интересов со всеми соавторами научных работ отсутствует.
Основное содержание работы
Во введении обосновывается актуальность темы диссертационной работы; формулируются цель и задачи исследований; представляются основные положения работы, выносимые на защиту; определяются научная новизна, теоретическая и практическая значимость полученных результатов; приводится краткая характеристика основных разделов диссертации.
Впервой главе выполнен аналитический обзор существующих типов задач раскроя и упаковки, а также основных методов их решения, приведена общая постановка задачи плотной упаковки и рассмотрены особенности и геометрические аспекты подходов, применяемых для решения различных задач этого класса.
Среди основных методов, применяемых для решения задач раскроя и упаковки можно выделить методы математического программирования, комбинаторной оптимизации, эвристические и метаэвристические методы. Методы математического программирования обеспечивают возможность получения решения задачи с заданной точностью, однако их применение ограничено лишь небольшими размерами задачи (как правило, до 20 объектов) ввиду их высокой вычислительной сложности. Методы комбинаторной оптимизации, основанные на выполнении частичного перебора различных вариантов решения задачи, также являются очень чувствительными к размерности задачи. Наилучший компромисс между скоростью решения и качеством решения в условиях единичного и мелкосерийного производства достигается при использовании эвристических и метаэвристических методов оптимизации. Для задач раскроя и упаковки наивысшую эффективность демонстрируют метаэвристические методы, основанные на эволюционных моделях оптимизации. Эвристические методы могут быть использованы как для выполнения однопроходной оценки возможности размещения объектов, так
идля их применения в составе других оптимизационных моделей. Решение задачи упаковки на основе эвристических и метаэвристических методов оптимизации может быть сведено к поиску последовательности объектов, размещение которых в соответствии с некоторым используемым правилом или эвристикой обеспечивает получение наиболее плотной компоновки.
Вдиссертационной работе рассматриваются вопросы повышения эффективности размещения ортогональных объектов в форме параллелепипедов различной размерности (в двухмерном случае – прямоугольников) и ортогональных многогранников на основе эвристических и метаэвристических алгоритмов. Ортогональный многогранник является
12
составным объектом, представленным в виде набора ортогональных объектов с фиксированным положением друг относительно друга, рассматриваемых в качестве единого целого. Несмотря на то, что разработанные автором алгоритмы позволяют решать задачи линейного раскроя и одномерной упаковки, в работе они не рассматриваются, с одной стороны, из-за простоты их геометрического описания, с другой стороны, благодаря наличию точных методов их решения и глубокой проработанности другими исследователями.
Ниже приведена общая постановка задачи плотной упаковки
ортогональных объектов произвольной размерности. |
|
|
|
|
|||||||
При решении задачи D -мерной ортогональной |
упаковки каждый |
||||||||||
контейнер j |
представлен в форме D -мерного параллелепипеда (отрезка при |
||||||||||
D =1 |
или |
прямоугольника |
при |
D = 2 ) |
с |
габаритными |
размерами |
||||
{W 1,W |
2 ,K,W D } |
(верхний индекс в формулах используется для обозначения |
|||||||||
j |
j |
j |
|
|
|
|
|
|
|
|
|
номера координатной оси). Ортогональный |
объект |
i |
задаётся |
D -мерным |
|||||||
параллелепипедом с габаритными размерами |
{w1, w2 ,K, wD |
}. Ортогональный |
|||||||||
|
|
|
|
|
|
i |
i |
|
i |
oi,k , k Î{1,K, mi } с |
|
многогранник Oi |
состоит из mi |
ортогональных объектов |
|||||||||
габаритными |
размерами {w1 |
, w2 |
,K, wD }, |
положение |
которых друг |
||||||
|
|
|
i,k |
i,k |
i,k |
|
|
|
|
|
|
относительно друга задаётся с помощью векторов {z1 |
, z 2 |
,K, z D } в локальной |
|||||||||
|
|
|
|
|
|
|
i,k |
i,k |
|
i,k |
|
системе координат, связанной с этим ортогональным многогранником. Положение объекта в D -мерном контейнере j определяется точкой D -мерного параллелепипеда, описанного вокруг этого объекта, которая расположена на минимальном расстоянии от начала координат контейнера
(обозначается |
через |
{x1 |
; x |
2 |
;K; x D |
для ортогонального |
объекта i и через |
||||
|
|
|
|
|
|
ij |
|
ij |
ij |
|
|
{X |
1 |
; X |
2 |
;K; X D |
для |
ортогонального многогранника O ; |
для единственного |
||||
|
ij |
|
ij |
ij |
|
|
|
|
|
i |
|
контейнера в нижнем индексе указывается только номер объекта). Число размещаемых объектов обозначается через n , число контейнеров – через N .
Для задачи плотной упаковки дополнительно может быть задан ряд физических параметров (максимально допустимая весовая нагрузка контейнера, вес объекта, положение физического центра тяжести), а также технологических параметров (например, величина припуска на раскрой).
Для обеспечения размещения объектов в требуемом направлении
контейнера задаётся |
направление загрузки в |
виде |
приоритетного |
списка |
L = {L1, L2 ,K, LD } |
( Ld {1,K, D} d {1,K, D}, |
Li |
¹ L j "i ¹ j ), |
который |
определяет порядок выбора координатных осей контейнера в процессе геометрического конструирования упаковки.
При решении задачи раскроя-упаковки объектов в несколько контейнеров целевой функцией является функция минимизации числа занятых объектами контейнеров. При размещении объектов в единственный контейнер минимизируется длина получаемой упаковки. Под длиной S упаковки понимается взятая на оси LD координата точки, которая принадлежит геометрической области упаковки и расположена максимально далеко от
13
начала координат контейнера вдоль оси LD . Плотность упаковки определяется как отношение объёма ортогонального параллелепипеда, описанного вокруг упаковки, к суммарному объёму размещённых объектов.
Для всех типов задач прямоугольного раскроя и ортогональной упаковки различной размерности должны совместно выполняться три геометрических условия корректного размещения объектов.
1.Рёбра всех размещённых в контейнере объектов должны давать ненулевую проекцию только на одну координатную ось контейнера.
2.Размещённые объекты не должны перекрывать друг друга, т.е. для
каждой пары |
ортогональных |
объектов |
|
i, h Î{1,K, n}, i ¹ h , |
размещённых в |
|||||||||||
контейнере j , должны выполняться условия: |
|
|
|
|
|
|
|
|||||||||
(xd ³ xd |
+ wd )Ú (xd |
|
³ xd + wd ) |
"j Î{1,K, N }, |
"d Î{1,K, D}. |
|
||||||||||
ij |
hj |
h |
hj |
|
ij |
i |
|
|
|
|
|
|
|
|
|
|
При решении задачи упаковки ортогональных многогранников для |
||||||||||||||||
каждой пары ортогональных многогранников |
Oi и |
Oh , |
i, h Î{1,K, n}, i ¹ h , |
|||||||||||||
размещённых в контейнере j , должны выполняться условия: |
|
|
|
|||||||||||||
(X d + z d |
³ X d |
+ z d |
+ wd |
|
)Ú (X d |
+ z d |
³ X d + z d |
+ wd |
) |
|||||||
|
ij |
i,k ′ |
hj |
|
|
h,k ′′ |
h,k ′′ |
|
hj |
h,k ′′ |
|
ij |
i,k ′ |
i,k ′ |
|
|
|
j {1,K, N }, |
|
|
d {1,K, D}, |
oi,k ′ Oi , |
oh,k ′′ Oh . |
|
|||||||||
3. Размещённые объекты не должны выходить за границы контейнеров. Для этого при решении задач прямоугольного раскроя и ортогональной
упаковки для каждого ортогонального объекта i {1,K, n}, размещённого в контейнере j , должны выполняться условия:
(xd ³ 0)Ù (xd + wd £ W d ) |
"j Î{1,K, N }, |
"d Î{1,K, D}. |
||||||||
ij |
ij |
i |
|
j |
|
|
|
|
|
|
При решении задачи прямоугольной упаковки в полубесконечный |
||||||||||
контейнер заданной |
ширины |
W 1 |
и |
бесконечной |
длины W 2 = ∞ должны |
|||||
выполняться условия: (x d ³ 0)Ù |
(x1 + w1 |
£ W 1 ) "d Î{1,2},"i Î{1,K,n}. |
||||||||
|
i |
|
|
i |
i |
|
|
|
|
|
При решении задачи упаковки ортогональных многогранников для |
||||||||||
каждого ортогонального многогранника Oi |
должны выполняться условия: |
|||||||||
|
(X d + z d |
³ 0)Ù (X d + z d |
+ wd |
£ W d ) |
||||||
|
|
ij |
i,k |
|
|
ij |
i,k |
|
i,k |
j |
j {1,K, N }, |
d {1,K, D}, oi,k Oi , |
i {1,K, n}. |
||||||||
Решение задачи представляется в виде строки натуральных чисел (строки размещения), которая определяет очерёдность размещения объектов или применения правил выбора объектов. При декодировании строки размещения осуществляется последовательный выбор каждого объекта с последующим его размещением (в зависимости от условий задачи и параметров, приведённых в данной строке, перед размещением объекта может выполняться его поворот).
В настоящее время для решения задач раскроя и упаковки объектов нерегулярной формы используются подходы, заключающиеся в представлении объектов в полигональном виде с последующим составлением и анализом годографов функций плотного размещения объектов. При этом процесс решения таких задач основан на применении методов нелинейного
14
программирования, которые на практике при увеличении числа размещаемых объектов и повышении степени их детализации оказываются неприменимыми из-за значительных затрат временных ресурсов, что делает актуальной проблему развития методов решения задач плотной упаковки объектов произвольной формы и различной размерности.
Вторая глава посвящена исследованию моделей геометрического конструирования пространства ортогональной упаковки произвольной размерности.
Проблема выбора эффективной модели для геометрического описания упаковки является крайне важной, поскольку она используется при формировании каждого промежуточного решения, что напрямую влияет на скорость и качество решения задачи в целом. Существующие способы геометрического описания ортогональной упаковки недостаточно проработаны, в частности: не рассмотрен вопрос получения множества минимальной мощности, состоящего из параллелепипедов заданной размерности, полностью описывающего всё свободное пространство контейнера; отсутствуют алгоритмы удаления ортогональных многогранников из упаковки с последующим обновлением свободного пространства контейнера произвольной размерности; отсутствуют методы и алгоритмы, обеспечивающие выбор наилучшей области для каждого размещаемого объекта на основе анализа всех свободных пространств внутри упаковки произвольной размерности.
Рассмотрены различные модели, используемые для геометрического описания ортогональной упаковки (рецепторная модель, узловая модель, блочная модель, модель виртуальных объектов). Особенности рецепторной модели, связанные с громоздкостью описания пространства контейнеров и значительными затратами вычислительных ресурсов, не позволяют применять её на практике при размещении большого числа объектов.
Разработана модель потенциальных контейнеров, обеспечивающая представление свободного пространства каждого контейнера в виде набора всех возможных ортогональных объектов с наибольшими габаритными размерами, которые могут быть в нём размещены (так называемых потенциальных контейнеров, ПК). Для корректного размещения ортогонального объекта внутри контейнера необходимо, чтобы он был размещён целиком внутри хотя бы одного потенциального контейнера.
|
|
|
Если в процессе размещения в точке |
||
{x1 |
, x |
2 |
,K, x D } |
контейнера |
D -мерный |
i |
|
i |
i |
|
|
ортогональный объект i будет перекрыт некоторым потенциальным контейнером k с габаритными размерами {p1k , pk2 ,K, pkD },
расположенным в точке {x1 |
, x |
2 |
,K, x D } |
k |
|
k |
k |
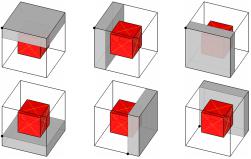
контейнера, то будут сформированы не более 2D новых потенциальных контейнеров из двух наборов (рисунок 1):
Рисунок 1. Потенциальные контейнеры, формируемые при размещении трёхмерного объекта

15
1) |
набор |
потенциальных |
контейнеров |
с |
габаритными |
|
размерами |
|||||||||
{p1 |
, p |
2 ,K, p d −1, x d |
− x d |
, p d +1 |
,K, p D |
, |
расположенных |
в |
|
точке |
||||||
k |
|
k |
k |
i |
k |
k |
|
k |
|
|
|
|
|
|
|
|
{x1k , xk2 ,K, xkd ,K, xkD }, |
при |
выполнении |
условий |
перекрытия |
|
xid |
> xkd и |
|||||||||
x d |
< x d |
+ p d |
d {1,K, D}; |
|
|
|
|
|
|
|
|
|
||||
i |
|
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
набор |
потенциальных |
контейнеров |
с |
габаритными |
|
размерами |
|||||||||
{p1 |
, p |
2 ,K, p d −1, x d |
+ p d |
− x d |
− wd , p d +1,K, p D }, |
расположенных |
|
в |
точках |
|||||||
k |
|
k |
k |
k |
|
k |
i |
i |
k |
|
k |
|
|
|
|
|
{x1 |
, x 2 ,K, x d −1, x d + wd |
, x d +1,K, x D |
}, |
при |
выполнении условий |
|
перекрытия |
|||||||||
k |
k |
k |
i |
i |
|
k |
k |
|
|
|
|
|
|
|
|
|
x d |
+ wd |
> x d |
и x d |
+ w d |
< x d |
+ p d |
d {1,K, D}. |
|
|
|
|
|
||||
i |
|
i |
k |
i |
|
i |
k |
k |
|
|
|
|
|
|
|
|
Модель потенциальных контейнеров описывает всё свободное пространство контейнера, что исключает вероятность образования неконтролируемых моделью локальных пустот контейнера. В процессе конструирования упаковки набор потенциальных контейнеров регулярно обновляется – из него удаляются все потенциальные контейнеры, которые частично или полностью перекрываются новым размещаемым объектом, а также добавляются новые потенциальные контейнеры, образованные в области размещения объекта. Для получения множества всех возможных потенциальных контейнеров минимальной мощности разработан алгоритм поиска и удаления вложенных потенциальных контейнеров. Блок-схема алгоритма размещения объектов, основанного на использовании модели потенциальных контейнеров, представлена на рисунке 2.
Рисунок 2. Блок-схема алгоритма размещения объектов

16
Для хранения наборов потенциальных контейнеров произвольной размерности предложена многоуровневая связная структура данных, которая
содержит |
набор K потенциальных контейнеров, расположенных в точках |
|||
{x1 |
, x |
2 |
,K , x D }, k K , в виде набора рекурсивно вложенных друг в друга на |
|
k |
|
k |
|
k |
различных уровнях линейных связных списков, содержащих элементы, упорядоченные по возрастанию уникальных значений (рисунок 3). Каждый
элемент j списка i на уровне вложенности Ld содержит координату siL, dj = xkLd
такого потенциального контейнера k , что внутри каждого связного списка
выполняется неравенство sLd |
|
|
< sLd |
d {1,K, D}. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i, j |
|
|
|
i, j +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
L : |
|
s Ld |
→K → s Ld →K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
1,1 |
|
|
|
|
1,i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
↓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
L |
+1 |
: |
|
|
|
|
|
|
|
|
s Ld +1 |
→K → s Ld +1 |
→K |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
i,1 |
|
|
|
|
i, j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
↓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
+2 |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s Ld +2 |
→K → s Ld +2 |
→K |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j,1 |
|
|
|
|
j,k |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Рисунок 3. Многоуровневая связная структура данных |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
На рисунке 4 представлен пример многоуровневой связной структуры |
||||||||||||||||||||||||||||||||||||||||
данных, |
хранящей |
набор |
|
|
потенциальных |
контейнеров |
|
из |
таблицы 1, |
|||||||||||||||||||||||||||||||||||||
упорядоченный в соответствии с направлением загрузки L = {1, 2,3}. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Координаты потенциальных |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
контейнеров |
|
|
|
|||||||
1 |
|
|
|
2 |
|
|
3 |
|
|
|
|
7 |
|
|
|
|
9 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
1 |
2 |
3 |
|
4 |
|
5 |
6 |
|
7 |
8 |
9 |
10 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
x1k |
|
0 |
0 |
0 |
2 |
2 |
2 |
2 |
4 |
4 |
4 |
|||
0 |
1 |
|
3 |
1 |
|
|
|
|
2 |
|
|
5 |
|
6 |
1 |
|
|
2 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
Рисунок 4. Многоуровневая связная структура |
|
xk2 |
|
1 |
2 |
2 |
|
3 |
|
7 |
7 |
|
9 |
1 |
1 |
1 |
||||||||||||||||||||||||||||
|
|
данных для направления загрузки L = {1, 2,3} |
|
xk3 |
|
0 |
1 |
3 |
|
1 |
|
2 |
5 |
|
6 |
1 |
2 |
3 |
||||||||||||||||||||||||||||
Исследование многоуровневой связной структуры данных проводилось на примере сравнения с упорядоченным одномерным линейным связным списком. Относительная временная эффективность многоуровневой связной структуры данных определялась как отношение времени размещения объектов при использовании линейного списка ко времени, затрачиваемого при использовании многоуровневого связного списка. Для всех тестовых задач двухмерной (S.P. Fekete, J. Schepers1) и трёхмерной (S. Martello, D. Pisinger, D. Vigo2) ортогональной упаковки предложенная структура данных обеспечивает более быстрое формирование упаковки по сравнению с одномерным линейным связным списком (рисунок 5).
1 http://people.brunel.ac.uk/~mastjjb/jeb/info.html
2 Martello, S. The three-dimensional bin packing problem / S. Martello, D. Pisinger, D. Vigo // Operations Research. – 2000. – Vol. 48, № 2. – P. 256–267.

|
|
|
17 |
|
|
|
|
|
|
Относительная временная эффективность |
2,00 |
|
|
Относительная временная эффективность |
4,00 |
3,64 |
1,50 |
50 объектов |
||
|
3,11 |
|
||||
|
|
100 объектов |
||||
3,00 |
2,002,27 |
1,00 |
||||
|
||||||
2,00 |
150 объектов |
|||||
1,231,49 |
0,50 |
|||||
|
||||||
1,09 |
200 объектов |
|||||
1,00 |
|
0,00 |
||||
|
|
|||||
|
|
|
||||
|
|
|
|
|||
|
0,00 |
|
|
I |
II III IV V VI VII VIII |
|
|
40 |
50 100 150 250 500 1000 |
|
Классызадачтрёхмернойортогональной |
||
|
Число размещаемых объектов |
|
|
упаковкиобъектов |
||
|
|
а) |
|
|
б) |
|
Рисунок 5. Относительная временная эффективность многоуровневой связной |
||||||
|
структуры данных в сравнении с линейным связным списком: |
|||||
а) задачи двухмерной упаковки; б) задачи трёхмерной ортогональной упаковки |
||||||
Важной особенностью многоуровневой связной структуры данных является рост относительной временной эффективности её применения с увеличением числа размещаемых объектов, что объясняется тем, что некоторые новые потенциальные контейнеры в проекциях на координатные оси будут иметь общие координаты с другими потенциальными контейнерами.
Анализ эффективности модели потенциальных контейнеров проводился при решении тестовых задач двухмерной прямоугольной упаковки (S.P. Fekete, J. Schepers) и трёхмерной ортогональной упаковки (S. Martello, D. Pisinger, D. Vigo). В качестве показателя качества размещения служит относительное отклонение μ от нижней границы решения, которое рассчитывается по
формуле μ(%)= (N * − Λ) n ×100% , где N * – число заполненных объектами контейнеров; Λ – точная нижняя граница задачи. Проведённые вычислительные эксперименты показали, что модель потенциальных контейнеров обеспечивает получение наилучших показателей размещения (как по плотности упаковки, так и по скорости её конструирования) в сравнении со всеми рассмотренными моделями геометрического описания упаковки на всех наборах тестовых задач различной размерности (рисунок 6).
n ×100% , где N * – число заполненных объектами контейнеров; Λ – точная нижняя граница задачи. Проведённые вычислительные эксперименты показали, что модель потенциальных контейнеров обеспечивает получение наилучших показателей размещения (как по плотности упаковки, так и по скорости её конструирования) в сравнении со всеми рассмотренными моделями геометрического описания упаковки на всех наборах тестовых задач различной размерности (рисунок 6).
Вычислительные эксперименты на тестовых задачах упаковки на полубесконечную полосу (E. Hopper, B.C.H. Turton3) показали, что оптимальные решения для всех тестовых задач достигаются только при использовании модели потенциальных контейнеров.
Получение эффективного инструмента для полного геометрического описания ортогональной упаковки произвольной размерности в виде модели потенциальных контейнеров делает возможным приведение задач раскроя- упаковки объектов произвольной формы и различной размерности к задачам упаковки ортогональных многогранников, созданных, в том числе, с использованием воксельной модели. В результате разработан универсальный метод решения различных типов NP-трудных задач раскроя и упаковки объектов сложной геометрии на основе структурной декомпозиции свободного пространства контейнеров произвольной формы с обобщением по размерности.
3 https://github.com/Oscar-Oliveira/OR-Datasets/tree/master/Cutting-and-Packing/2D/Datasets/HT2001a

18
а)
μ, %
в)
Время, с
2,50
2,00
1,50
1,00
1 |
2 |
3 |
Типы задач NGCUTFS
50,0
40,0
30,0
20,0
10,0
0,0
1 |
2 |
3 |
Типы задач NGCUTFS
 Узловая модель
Узловая модель
 Блочнаямодель
Блочнаямодель
 Модель виртуальных объектов
Модель виртуальных объектов  Модель потенциальных контейнеров
Модель потенциальных контейнеров
б) |
20,0 |
|
|
|
|
|
, % |
15,0 |
|
|
|
|
|
10,0 |
|
|
|
|
|
|
μ |
5,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0 |
|
|
|
|
|
|
I |
II |
III IV |
V |
VI |
VII VIII |
|
|
|
Класс задач |
|
||
г) |
|
15,0 |
|
|
|
|
|
|
|
, с |
10,0 |
|
|
|
|
|
|
|
Время |
|
|
|
|
|
|
|
|
5,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0 |
|
|
|
|
|
|
|
|
I |
II |
III |
IV |
V |
VI |
VII VIII |
|
|
|
|
|
Класс задач |
|
||
 Узловая модель
Узловая модель
 Блочнаямодель
Блочнаямодель
 Модель виртуальных объектов
Модель виртуальных объектов  Модель потенциальных контейнеров
Модель потенциальных контейнеров
Рисунок 6. Результаты тестирования моделей геометрического описания упаковки: а) качество размещения (задачи двухмерной упаковки); б) качество размещения (задачи трёхмерной упаковки); в) скорость размещения (задачи двухмерной упаковки); г) скорость размещения (задачи трёхмерной упаковки)
В третьей главе рассматриваются вопросы разработки и анализа эвристических и метаэвристических методов решения задач раскроя-упаковки.
При решении задач раскроя-упаковки традиционно используются строки размещения, содержащие номера последовательно выбираемых к размещению объектов, однако такой подход не всегда оказывается эффективным, особенно при увеличении числа размещаемых объектов. Одной из перспективных технологий оптимизации решения NP-трудных задач является мультиметодная технология (предложена профессором И.П. Норенковым4), в основу которой положена идея кодирования решения задачи в виде последовательности
элементарных алгоритмов решения задачи (эвристик). |
|
|
||||||||
|
Для задач двухмерной прямоугольной упаковки разработаны четыре |
|||||||||
эвристики размещения. |
|
|
|
|
|
|
|
|||
|
1. Эвристика BWF («Best Width Fit» – «наилучший подходящий по |
|||||||||
ширине»): поиск наиболее подходящего объекта i |
(с габаритными размерами |
|||||||||
{w1, w2}) для его размещения в заданном ПК k |
(с габаритными размерами |
|||||||||
i |
i |
|
|
|
|
|
|
|
|
|
{p1 |
, p2}) вдоль оси L |
2 |
контейнера: |
(p L2 − wL2 |
)→ min, wd ≤ pd d {1, 2}. |
|||||
k |
k |
|
k |
i |
|
|
i |
k |
|
|
|
2. Эвристика BSF («Best Square Fit» – «наилучший подходящий по |
|||||||||
площади»): поиск наиболее подходящего объекта i |
с максимальной площадью |
|||||||||
для его размещения в заданном ПК k : |
(p1 p |
2 |
− w1w2 )→ min, wd |
≤ p d d {1, 2}. |
||||||
|
|
|
|
|
k |
k |
i i |
|
i |
k |
4 Норенков, И.П. Эвристики и их комбинации в генетических методах дискретной оптимизации / И.П. Норенков // Информационные технологии. – 1999. – № 1. – С. 2–7.
19
3. Эвристика FWF («First Width Fit» – «первый подходящий по ширине»):
поиск |
первого |
подходящего |
|
ПК |
k : |
|
j < k d |
* {1,2}: pd * < wd * , |
||
|
|
|
|
|
|
|
|
|
j |
i |
wd |
≤ p d d {1, 2}, |
ближайшего |
к |
началу |
координат |
контейнера, |
для |
|||
i |
|
k |
|
|
|
|
|
|
|
|
размещения в нём первого объекта i |
из списка πw неразмещённых объектов, |
|||||||||
упорядоченных по убыванию габаритных размеров вдоль оси L2 контейнера. |
||||||||||
|
|
4. Эвристика |
FSF («First |
Square |
Fit» |
– |
«первый |
подходящий |
по |
|
площади»): поиск первого подходящего ПК |
k : |
j < k d |
* {1,2}: pd * < wd * , |
|||||||
|
|
|
|
|
|
|
|
|
j |
i |
wd |
≤ p d d {1, 2}, |
ближайшего |
к |
началу |
координат |
контейнера, |
для |
|||
i |
|
k |
|
|
|
|
|
|
|
|
размещения в нём первого объекта i |
из списка πs |
неразмещённых объектов, |
||||||||
упорядоченных убыванию их площадей. |
|
|
|
|
|
|||||
Мультиметодный генетический алгоритм, использующий разработанные эвристики, превосходит по качеству размещения объектов классический генетический алгоритм, а также другие варианты реализации генетического алгоритма на всех классах тестовых задач S.P. Fekete, J. Schepers.
Для задач трёхмерной упаковки разработаны эвристики размещения (таблица 2), основанные на использовании пар правил выбора неразмещённых
объектов (O |
1 |
K O |
5 |
) |
и потенциальных |
контейнеров |
|
( P K P ), что |
делает |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
7 |
|
|
|
||
возможным формирование 35 различных эвристик. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
||
|
|
Правила выбора объектов и ПК для задач трёхмерной упаковки |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
O1 |
Выбор |
неразмещённого |
объекта |
с |
P4 |
|
Выбор |
подходящего ПК, для которого |
|||||||||||||||
|
|
максимальным объёмом. |
|
|
|
|
|
p L1 p L2 |
→ max и p L3 → min . |
|
|
||||||||||||
O |
2 |
Выбор |
неразмещённого |
объекта |
с |
P |
|
Выбор |
подходящего ПК, для которого |
||||||||||||||
|
минимальным объёмом. |
|
|
|
5 |
|
|
|
→ min и p L3 → max . |
|
|
||||||||||||
|
|
|
|
|
|
|
p L1 p L2 |
|
|
||||||||||||||
O |
Выбор |
первого |
|
объекта из |
набора |
P |
|
Выбор |
наиболее |
подходящего |
ПК |
с |
|||||||||||
|
3 |
упорядоченных по убыванию размеров |
6 |
|
|
|
|
|
|
|
|
|
− wL1 . |
||||||||||
|
|
|
|
минимальным |
значением |
p L1 |
|||||||||||||||||
|
|
объектов в соответствии со списком L . |
|
|
Если таких ПК несколько, выбрать среди |
||||||||||||||||||
O |
|
Выбор первого объекта, |
для которого |
|
|
||||||||||||||||||
4 |
|
|
них |
ПК |
с |
|
минимальным |
значением |
|||||||||||||||
|
|
→ max и w L3 → min . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
w L1 w L2 |
|
|
|
p L2 |
− wL2 . |
Если |
таких ПК |
несколько, |
|||||||||||||
O |
5 |
Выбор первого объекта, |
для которого |
|
|
выбрать среди них ПК с минимальным |
|||||||||||||||||
|
|
→ min и w L3 → max . |
|
|
|
значением p L3 |
− wL3 . |
|
|
|
|||||||||||||
|
|
w L1 w L2 |
|
|
|
|
|
|
|||||||||||||||
P |
Выбор |
первого |
|
подходящего |
ПК |
с |
P |
|
Выбор |
наиболее |
подходящего |
ПК |
с |
||||||||||
1 |
максимальным объёмом. |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
− wL3 . |
||||||||
|
|
|
|
|
|
|
максимальным |
значением |
p L3 |
||||||||||||||
P |
|
Выбор |
первого |
|
подходящего |
ПК |
с |
|
|
Если таких ПК несколько, выбрать среди |
|||||||||||||
2 |
минимальным объёмом. |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
них |
ПК |
с |
максимальным |
значением |
||||||||||||
P3 |
Выбор первого подходящего ПК из |
|
|
p L2 |
− wL2 . |
Если |
таких ПК |
несколько, |
|||||||||||||||
|
|
набора упорядоченных по возрастанию |
|
|
выбрать среди них ПК с максимальным |
||||||||||||||||||
|
|
координат ПК |
|
в |
соответствии |
со |
|
|
|||||||||||||||
|
|
|
|
|
значением |
p L1 |
− wL1 . |
|
|
|
|||||||||||||
|
|
списком L . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20
Проведённые вычислительные эксперименты на тестовых задачах трёхмерной ортогональной упаковки (S. Martello, D. Pisinger, D. Vigo) показали, что правила O1 , O3 и O4 обеспечивают примерно одинаковое качество размещения. Наибольшую эффективность обеспечивает правило O1 , в то время, как правила O2 и O5 обеспечивают наихудшее размещение объектов на всех классах тестовых задач. При использовании правил O2 и O5 затрачивается время, на порядок большее по сравнению с остальными правилами выбора объектов. Все правила выбора потенциальных контейнеров обеспечивают в среднем одинаковое качество размещения, однако правила P6 и P7 затрачивают время, большее (в среднем) в 2–3 раза в сравнении со всеми остальными правилами. На основе полученных результатов тестирования были определены вероятности включения различных правил в эвристики для мультиметодного генетического алгоритма (таблица 3), который использует хромосомы, представленные последовательностями применяемых эвристик.
Таблица 3
Вероятности включения правил выбора объектов и потенциальных контейнеров в эвристики для мультиметодного генетического алгоритма
Правило |
O |
1 |
O |
2 |
O |
O |
4 |
O |
5 |
P |
P |
P |
P |
P |
P |
P |
|
|
|
3 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||||
Вероятность |
90% |
1% |
3% |
5% |
1% |
18% |
18% |
26% |
18% |
18% |
1% |
1% |
||||
В таблице 4 приведены тестирования мультиметодного генетического алгоритма с разработанными эвристиками (МГА) на тестовых задачах трёхмерной ортогональной упаковки 3DBPP (S. Martello, D. Pisinger, D. Vigo), а
также результаты решения этих задач следующими алгоритмами (наилучшие решения в таблице выделены полужирным шрифтом и курсивом):
−O1 P3 – эвристика, использующая правила O1 и P3 ;
−C-EPBFD – эвристический алгоритм размещения по экстремальным
точкам (T.G. Crainic, G. Perboli, R. Tadei);
−MPV-BS – метод ветвей и границ (S. Martello, D. Pisinger, D. Vigo);
−HA – эвристика Height first – Area second (A. Lodi, S. Martello, D. Vigo);
−LB – нижняя граница, вероятностно рассчитанная M.A. Boschetti.
Таблица 4
Результаты тестирования эвристик и мультиметодного генетического алгоритма на тестовых задачах трёхмерной ортогональной упаковки
Класс задач |
МГА |
Лучшая |
O1P3 |
C-EPBFD |
MPV-BS |
HA |
LB |
эвристика |
|||||||
Класс I |
129,2 |
131,3 |
131,3 |
130,5 |
133,3 |
132,3 |
124,0 |
Класс IV |
297,4 |
300,2 |
300,2 |
294,0 |
295,0 |
294,3 |
292,2 |
Класс V |
66,9 |
68,7 |
68,8 |
72,6 |
81,5 |
73,6 |
66,4 |
Класс VI |
97,1 |
98,7 |
99,0 |
98,1 |
106,5 |
100,2 |
93,0 |
Класс VII |
63,0 |
64,3 |
64,9 |
62,8 |
68,2 |
63,7 |
55,4 |
Класс VIII |
83,5 |
84,6 |
84,9 |
85,4 |
90,9 |
87,1 |
77,8 |
ИТОГО |
737,1 |
747,8 |
749,1 |
743,4 |
775,4 |
751,2 |
708,8 |
