9427

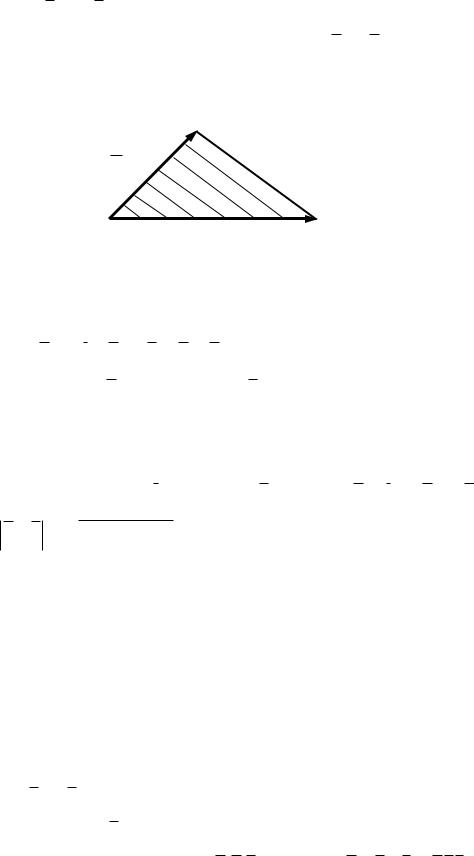
Следовательно, площадь треугольника, построенного на

векторах a и b (рис. 2.8) равна половине модуля векторного произведения, построенного на векторах a и b :

b

Пример. Найти площадь треугольника, построенного на векторах a 2i k и b j k .

Решение. a 2;0 1 и b 0;1; 1 . Тогда

0 1 i 2 0 j 2 0 k i 2 j 2k ; a b 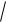12 22 22 3 , следовательно

вектора a и b умножаются векторно, а их результат - скалярно на третий вектор c . Такое произведение векторов называется смешанным и обозначается a b c , то есть a b c abc .

20

Смешанное произведение трех векторов a , b и c

представляет собой число, равное объему параллелепипеда, построенного на этих векторах (рис. 2.9), взятое со знаком «плюс», если эти три вектора образуют правую тройку и со знаком «минус», если они образуют левую тройку векторов.

c

b

Свойства смешанного произведения

1)a b c b c a c a b;

2)a b c a b c ;

3)a b c a c b ; a b c b a c , a b c c b a ;

4)Если a b c 0, то векторы a , b и c компланарны.

Смешанное произведение трех векторов a , b и c ,

Пример. Вычислить смешанное произведение векторов a 2i j , b j k , c i j k .

Решение. a 2; 1;0 , b 0;1; 1 , c 1;1;1 . Тогда

21

Ответ: a b c 5.

Исходя из геометрического смысла смешанного произведения, имеем, что объем параллелепипеда, построенного на векторах a , b и c (рис. 2.9) вычисляется по формуле

Vnap. abc .

Объем треугольной пирамиды, построенной на трех векторах a , b и c (рис. 2.10) вычисляется по формуле

Vnup. 16 a b c .

a c

b

Рис. 2.10

Пример. Найти объем пирамиды, построенной на векторах a 1; 2;3 , b 0;1; 1 и c 0; 1;0 .

Решение.

22

§ 3. Прямая линия на плоскости

Переходим к изучению прямой линии на плоскости. В аналитической геометрии фигуры описывают формулами. Введение на плоскости прямоугольной декартовой системы координат позволяет определять положение точки на плоскости заданием двух чисел – ее координат, а положение прямой на плоскости определять с помощью уравнения, то есть равенства, связывающего координаты точек прямой.

Исследование уравнения прямой позволяет аналитически проводить изучение геометрических свойств прямой. Так, для того, чтобы установить, лежит ли точка на прямой F x, y 0, достаточно проверить (не прибегая к геометрическим

3 1 2 1 3 1 2 0.

Следовательно, точка M 0 не лежит на данной прямой l .

Общее уравнение прямой

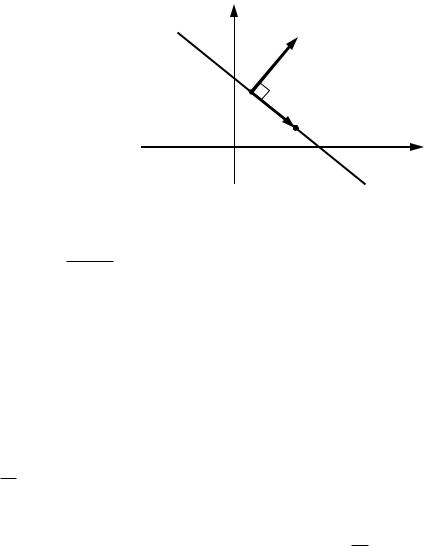
Пусть в прямоугольной декартовой системе координат на плоскости xOy задана точка M 0 x0 ; y0 и вектор N A; B . Требуется составить уравнение прямой l , проходящей через точку M 0 и перпендикулярной вектору N . (рис. 3.1)

23

Выберем произвольную точку M x; y на прямой l . Тогда вектор M0 M x x0 ; y y0 лежит на прямой l . Так как прямая l

Уравнение (3.1) является уравнением прямой на плоскости, проходящей через точку x0 ; y0 и перпендикулярной вектору

N A; B .

Всякий вектор, перпендикулярный прямой называется вектором нормали прямой. Вектор N A; B является вектором нормали прямой l .

Пример. Составить уравнение прямой l , проходящей через

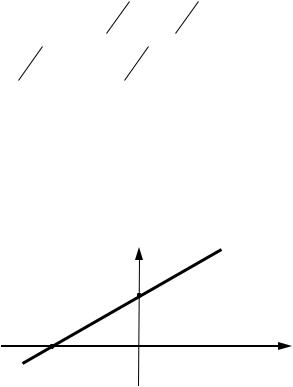
Ответ: x y 1 0 .

Преобразуем уравнение (3.1) следующим образом:

Исследуем уравнение (3.2):

1. При A 0, B 0, C 0 уравнение (3.2) примет вид

Ax By C .

Разделив обе части последнего уравнения на C

где a и b - величины отрезков, которые прямая l отсекает от осей координат (рис. 3.2).

Пример. Составить уравнение прямой l , проходящей через точку M 0 1; 2 и отсекающей от осей координат равные отрезки

(рис. 3.3).

25

y

l

b

2 M 0

Рис. 3.3

Следовательно, l : x y 3 – уравнение искомой прямой.

Ответ: x y 3 .

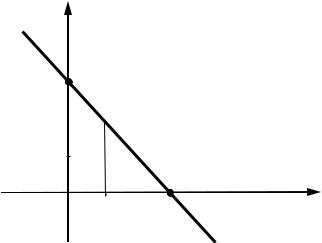
Пример. Построить прямую l : 2x 3y 6 0.

Решение. Приведем заданное уравнение к уравнению вида

(3.3):

через эти точки проведем прямую. Это и будет искомая прямая

(рис. 3.4).

26

y

-2

Рис.3.4

Если B 0, то уравнение (3.2) можно переписать и другим образом:

Угловой коэффициент k равен тангенсу угла наклона прямой l к положительному направлению оси Ox (рис. 3.5), то есть k tg .

y

27

Пример. Составить уравнение прямой l , проходящей через точку M 0 1; 2 и образующей с положительным направлением оси Ox угол 45 .

Решение. Пусть искомое уравнение прямой l запишется в

направление характеризуется угловым коэффициентом k , тогда уравнение этой прямой можно записать в виде:

l : y kx b,

также уравнением пучка прямых с центром в точке M 0 x0 ; y0 .

Из этого пучка нельзя определить лишь прямую, параллельную оси Oy , так как tg90 .

28

Пример. Составить уравнение прямой l , проходящей через точку пересечения прямых l1 : x y 2 0 и l2 : 2x y 5 0 и образующей с положительным направлением оси Ox угол 135 .

Решение. Координаты точки M 0 пересечения прямых l1 и l2

находим из системы уравнений этих прямых

x y 2 02x y 5 0

Получаем координаты точки M 0 1;3 .

По условию 135 , значит k tg135 1. Подставляя в уравнение (3.5) k 1 и x0 1, y0 3 находим искомое уравнение прямой

l : y 3 1 x 1 или l : x y 4 0.

Ответ: x y 4 0 .

Ax By 0.

Это уравнение прямой l , проходящей через начало координат –

29