9298

31

Этап 3. Находится точка Ê пересечения заданной прямой à c найденной на втором этапе прямой b. Сначала точка отмечается на плоскости Ï1: Ê1 = à1 Ç b1, затем по линии связи находится Ê2 Î à2.

В результате этих трех этапов найдена точка Ê (Ê1; Ê2) пересечения прямой общего положения à с плоскостью общего положения α. Очевидно, что в найденной точке Ê (Ê1; Ê2) пересечения прямой с плоскостью меняется видимость прямой.

Видимость определяется по методу конкурирующих точек в два этапа, результаты которых показаны на Рис. 14 б.

Этап 4. Определяется видимость прямой à1 относительно α1 на горизонтальной плоскости проекций Ï1. На Ï1 возьмем пару конкурирующих точек 3, 4 , принадлежащих скрещивающимся прямой à1 и

прямой m1, принадлежащей α1. Пусть 3 m и 4 a. На Ï1 проекции этих точек 31 и 41 совпадают. Вопрос видимости для 31 и 41 решается на Ï2, где их проекции разнесены. На Ï2 проекция точки 32 расположена выше проекции 42 (координата z3 > z4), следовательно, точка 3 расположена в пространстве выше точки 4 и прикрывает ее собой. Таким образом, на плоскости Ï1 видна проекция точки 31 и прямая m1, к которой она относится, следовательно видна α1. Невидимая на Ï1 проекция 41 принадлежит прямой à1, следовательно прямая невидима и обозначается штриховой линией.

Этап 5. Теперь определим видимость проекции à2 относительно α2 на Ï2 Для этого в качестве конкурирующих выберем точку 2,

принадлежащую прямой n, а значит плоскости α, и точку 5, принадлежащую прямой a. Вопрос видимости для 22 и 52 решается на Ï1, где их проекции разнесены. Посмотрим на Ï1 глубина какой точки больше?

Для этого сравним координаты y точек 21 и 51. y5 > y2, то есть глубина точки 5 больше, следовательно, 52 видима. Отметим скобками, что проекция 22,

32

которая принадлежит прямой n2, невидима. Значит, прямая a2 в этом месте находится перед плоскостью, она будет видима.

Используем приведенный алгоритм для решения задачи расчетно-

графической задачи.

Построим линию пересечения поверхности многогранника Ô (ABCS)

с плоскостью, ограниченной отсеком α ( LMN). Определим видимость на плоскостях проекций. Для этого решим последовательно задачи пресечения каждого ребра с плоскостью.

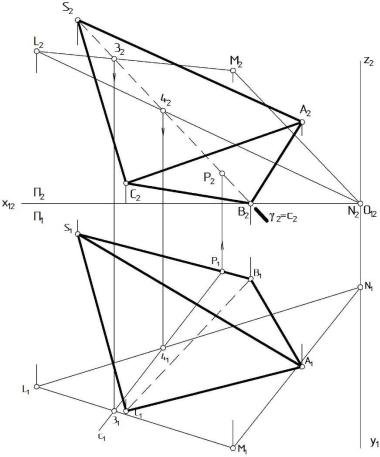
На комплексном чертеже (Рис. 15) показаны вспомогательные построения, в результате которых определяется точка Ê пересечения ребрa

пирамиды [SA] с плоскостью α ( LMN).

Этап 1.1. Ребро многогранника [SA] заключают во вспомогательную проецирующую плоскость-посредник β( β2 ) Ï2, которая на чертеже задается фронтальным следом β2. След совпадает с проекцией ребра

β2 = [S2A2].

33

Рисунок 59

Этап 1.2. Находится линия пересечения b вспомогательной плоскости-посредника β с заданной плоскостью α: b(12) = β Ç α. Проекции ребра в этом этапе не участвуют. Фронтальная проекция b2 совпадает со следом плоскости-посредника β2 = b2 и пересекает стороны треугольника

DLMN в точках 12 , 22: 12 = β2 Ç [L2M2]; 22 = β2 Ç [M2N2]. Горизонтальные проекции этих точек строятся по линии связи: 11 Î [L1M1]; 21 Î [M1N1]. Отрезок 1121 прямой b1, одновременно принадлежит обеим плоскостям и, следовательно, является линией их пересечения.

Этап 1.3. Находится точка Ê пересечения ребра [SA] с найденной на

34

ребро), затем по линии связи находится Ê2 Î [S2A2] (так же на продолжении ребра).

В результате этих трех этапов найдена точка Ê (Ê1; Ê2) пересечения ребра с плоскостью общего положения α. Ê (Ê1; Ê2) =[SA] Ça(DLMN).

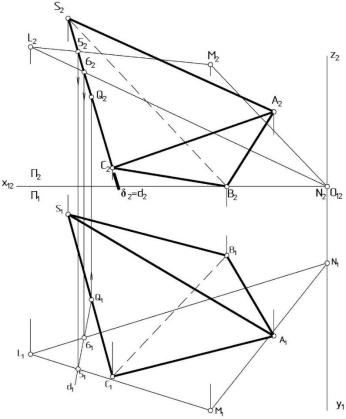
На комплексном чертеже (Рис. 16) показаны вспомогательные построения, в результате которых определяется точка пересечения ребрa [SB] пирамиды с плоскостью α (DLMN).

Рисунок 16

Этап 2.1. γ( γ2 ) ^ Ï2, которая на чертеже задается фронтальным следом β2. След совпадает с проекцией ребра γ2 = [S2B2].

Этап 2.2. c(34) = γ Ç α; γ2 = ñ2: 32 = γ2 Ç [L2M2]; 42 = β2 Ç [L2N2].

31 Î [L1M1]; 41 Î [L1N1].

Этап 2.3. P1 = [S1B1] Ç c1, P2 Î [S2B2] P (P1; P2) = [SB] Ç α(DLMN).

35

На комплексном чертеже (Рис. 17) показано определение точки пересечения ребрa [SC] пирамиды с плоскостью α (DLMN).

Рисунок 17

Этап 3.1. δ( δ2 ) ^ Ï2, δ2 = [S2C2].

Этап 3.2. d(56) = δ Ç α; δ2 = d2: 52 = δ2 Ç [L2M2]; 62 = δ2 Ç [L2N2].

51 Î [L1M1]; 61 Î [L1N1].

Этап 3.3. Q1 = [S1C1] Ç d1, Q2 Î [S2C2] Q (Q1; Q2) = [SC] Ç α(DLMN).

Замечание: если пирамида четырехугольная, необходимо повторить эти три этапа еще раз. Если боковые ребра не пересекают плоскости, следует рассмотреть ребра, входящие в основание многогранника.

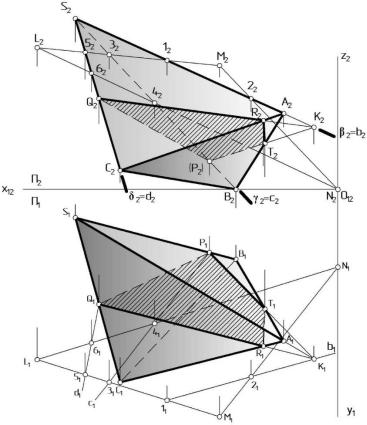
Соединив построенные точки K, P, Q прямыми, получим ломаную линию сечения боковой поверхности многогранника (Рис. 18). Однако боковая поверхность многогранника не бесконечна, а ограничена плоскостью основания DÀÂÑ, поэтому из полученной линии сечения KPQ поверхности пирамиды принадлежит часть, ограниченная ломаной QRTP

36

(заштрихована), где точки R и T принадлежат плоскости основания ÀÂÑ

(Рис. 17).

Рисунок 18

Рассмотрим получение точек R и T. Соединив точки сечения K и P прямой, получим линию, принадлежащую плоскости SAÂ. При пересечении прямой (KP) с ребром [AÂ], получим точку T. Отрезок [RÒ]

принадлежит грани SAÂ пирамиды. Аналогично (KQ) Ç [CA] = R; [RQ]

принадлежит грани DSAC. Отрезок [RT] принадлежит основанию DABC.

3.2. Построение линии пересечения многогранника заданной

плоскостью общего положения с применением преобразования

комплексного чертежа

Исходные проекции данных поверхности и секущей плоскости α преобразуются так, чтобы α приняла частное положение, т.е. выполняется преобразование плоскости общего положения в проецирующую, например,

37

α (DLMN) – о.п. ® α (DLMN) ^Ï4 (Рис. 19).

Рисунок 19

Заменим Ï2, на Ï4, перпендикулярную Ï1 и опорной прямой – горизонтали h данной плоскости α. Положение плоскости Ï4 однозначно определится осью õ14 = Ï1 Ç Ï4 .

Замечание: В качестве опорной прямой вместо горизонтали можно использовать фронталь f плоскости, решение при этом будет соответствовать замене Ï1 ® Ï4.

Порядок получения нового изображения плоскости следующий:

· строят проекции горизонтали плоскости h(h1; h2) Î α ;

38

·на плоскости Ï1 выбирают положение оси õ14 перпендикулярно

горизонтальной проекции горизонтали плоскости h1: õ14 ^ h1;

·проводят линии связи от точек L1, M1, N1, перпендикулярно новой оси õ14;

·откладывают от оси õ14 высоты точек zL, zM, zN, взятые с плоскости Ï2 (отмечено штрихами), высота точки N zN=0, поэтому N4 лежит на оси;

·полученные проекции индексируют L4, M4, N4;

соединив проекции L4, M4, N4, получают изображение плоскости α4. В соответствии с инвариантным свойством проецирования если фигура перпендикулярна плоскости проекций Ï4, то проекция фигуры полностью совпадает со следом плоскости: (L4, M4, N4) Ì α4.Аналогично построим новые проекции вершин многогранника S4, À4, Â4, C4. Соединив их, получим проекцию многогранника на плоскости Ï4 (Рис. 20).

Для определения видимости ребер многогранника на плоскости Ï4 используется метод конкурирующих точек в системе плоскостей Ï4/Ï1 аналогично системе Ï2/Ï1 .

Полученные на плоскости Ï4 точки пересечения ребер пирамиды со следом плоскости α4 (P4 = S4B4 Ç α4; T4 = À4B4 Ç α4; R4 = À4B4 Ç α4; Q4 = S4C4 Ç α4) обратным проецированием переносятся последовательно на исходные проекции тех же ребер: на Ï1 по линиям связи, перпендикулярным õ14 – P1, T1, R1, Q1, затем на Ï2 по линиям связи, перпендикулярным õ12 – P2, T2, R2, Q2.

Соединив построенные точки P, T, R, Q прямыми, получим ломаную линию сечения.

39

Рисунок 20

4.Определение видимости сечения

Определение видимости сечения следует выполнять после определения собственной видимости ребер многогранника.

При соединении точек ломаной сечения следует руководствоваться видимостью соответствующих граней: в видимой грани лежит видимая

40

и соответственно прямая Q2(P2) S2B2Ñ2.

Замечание: после определения видимости линии сечения, в случае необходимости, обозначения невидимых точек сечения заключают в скобки. Например, (Ð2).

5. Определение относительной видимости многогранника и секущей плоскости

Определение относительной видимости многогранника и плоскости

αнеобходимо вести с учетом непрозрачности.

Взонах не наложения отсека плоскости и пирамиды обе фигуры

видимы.

Видимость в границах наложения проекций пирамиды и плоскости определяется из чертежа исходя из следующих закономерностей:

∙часть прямой, принадлежащей плоскости, заключенная между точками пересечения с контуром сечения, находится внутри многогранника и, следовательно, не видна;

∙прямая, не пересекающаяся с контуром сечения, находится вне многогранника, ее видимость определяется методом конкурирующих точек.

Например (Рис. 21), часть прямой [LN] пересекает контур сечения в точках 8 и 9. Участок [89] прямой [LN] находится внутри многогранника и, следовательно, не виден Ï1 и Ï2. Видимость оставшихся прямых плоскости

αна Ï2 определена при помощи пары конкурирующих точек 3 и 3’(32 = 3’2),

одна из которых принадлежит прямой [L2M2] плоскости α, а другая ребру пирамиды. Горизонтальная проекция точки 3 (31) имеет большую координату y, чем проекция точки 3’ (3’1), следовательно, прямая [L2M2] видима, в этой зоне плоскость закрывает пирамиду.