9175

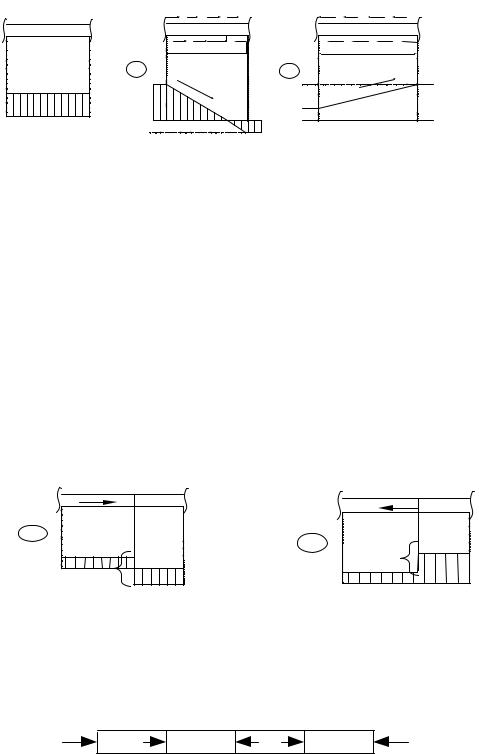
Рис. 3.6

Кроме того, из (1.4) следует, что если нагрузка qz положительна (направлена впра-

во), то на участке наблюдается уменьшение усилия N. Если qz отрицательна (направлена влево) - усилие N увеличивается. Причем изменение усилия N равняется (как это следует из 1.1) равнодействующей распределенной нагрузки qz. В сечении, в котором действует сосредоточенная продольная нагрузка F, имеет место скачкообразное изменение про-

дольного усилия N («скачок»). Это вытекает из зависимости 5. Изменение усилия N равно величине внешней силы F.

При положительной нагрузке F усилие N равно величине внешней силы F (направлен-

ной вправо), усилие N уменьшается на величину F.

При отрицательной (направленной влево) - увеличивается на величину F (puc. 3.7).

Рис. 3.7

3.2.3. Примеры решения задач на построение эпюр при ЦРС

Задача 1. Построить эпюру продольных сил для стержня, изображенного на рис. 3.8.

Рис. 3.8.

Решение

1. Опоры на рис. 3.8 не показаны, поэтому определять неизвестные реакции не требуется. Надо думать, что либо F1, либо F5, либо обе эти силы и являются реакциями,

которые были найдены заранее.

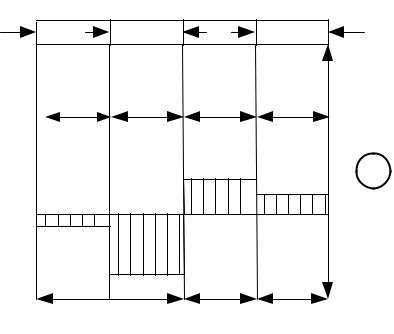
Все силы, приложенные к телу, должны находиться в равновесии. В противном случае оно начинает движение с ускорением, что недопустимо для элемента строитель-

ной конструкции. Проверим равновесие сил в данном случае

∑z=F1+F2 –F3 +F4 –F5 = 10+30-70+50-20=90-90=0 .

Равновесие есть.

2. Нумеруем участки. На каждом из них произвольно показываем сечение.

Рассматривая либо левую, либо правую часть стержня, вычислим значение уси-

лия N, учитывая формулу (1.1):

3. Строим график N(z), учитывая то, что на каждом из участков усилие N постоянно.

Убедимся для проверки, что высота и направление «скачков» на графике соответствует внешней нагрузке.

Из рис. 8, в частности, видно, что все участки стержня, за исключением участка № 3, сжаты, наиболее нагруженным является участок № 2 . Сжимающее усилие в нем равно 40 кН (около 4-х тонн).

Задача 3.2. Построить эпюру продольных сил для стержня, изображенного на рис.3.10 при следующих значениях нагрузок:

F1= 40 кН, F2= 10кН, F3= 20 кН, q1= 30кН/м, q2 = 5кН/м .

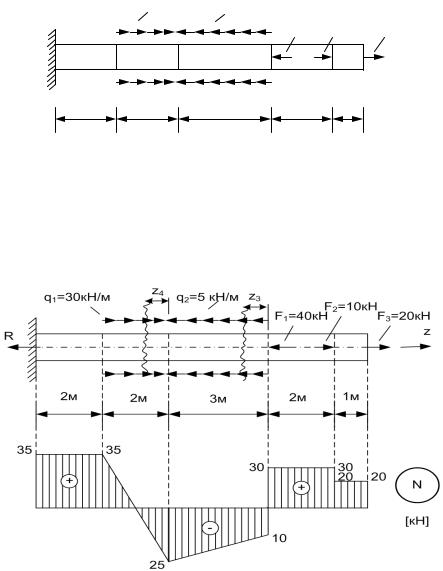
Рис. 3.10

Решение

1.Определим неизвестную опорную реакцию R, составив уравнение равновесия для всего стержня:

2.∑Z = 0, - R – F 1 + F2 + F3 + q1·2 - q2·3 = 0, R= - 40+ 10+ 20+ 30·2 – 5·3=+ 35 кН.

Рис. 3.11

2. Пронумеруем участки стержня (по направлению к заделке). В произвольном месте на каждом участке отметим поперечное сечение. Рассматривая либо левую, либо правую часть стержня, запишем выражение для продольной силы N на каждом участке.

На участках без распределенной нагрузки усилие N постоянно и не зависит от того,

в каком месте находится рассматриваемое сечение. На участках, где приложена распреде-

ленная нагрузка, от расположения сечения зависит, какая часть распределенной нагрузки придется на отсеченную часть стержня.

Другими словами, усилие N будет зависеть от расположения сечения (в данном случае линейно). Чтобы это учесть, расположение сечения будем отмечать переменным расстоянием, которое можно отсчитывать от края рассматриваемой части стержня (z3 ‒

для 3-го участка и z4 ‒ для 4-го участка).

При рассмотрении участков 1, 2, 3, 4 будем отбрасывать левую часть стержня. 1 участок. N1=F3= +20 кН (растяжение).

2 участок. N2 = F2+ F3 = 10 +20 =30 кН (растяжение).

3 участок. z3 изменяется от 0м до 3м (область определения N3) .

N3 = F3+ F2– F1- q2– z3 = 10 + 20 - 40 - 5z3= -10 - 5z3

Строим график функции N3 = -10 – 5 z3 (наклонная прямая).

График наклонной прямой обычно строят, подсчитав значения функции при

двух значениях аргумента, то есть, проводя ее через две точки. В данном случае

удобно определять ее значения на границах участка.

При z3 = 0м (правый край участка) N3 = -10-5·0 = -10 кН;

при z3 = 3 м (левый край участка) N3 = -10-5·3 = -25 кН. 4 участок. 0м ≤ Z4 ≤ 2м (область определения N4)

N4 = F3+ F2– F 1– q 2 3 + q1z4=20+10-40-5 3 + 30- z4= -25 + 30 z4.

При z4 = 0 м N4 = - 25 + 30 0 = - 25 кН;

при z4 =2 м N4 = - 25 + 30 2 = +35 кН.

При рассмотрении 5-го участка легче считать силы, приложенные к левой части

стержня.

5 участок. N5 = + R= + 35 кН.

3. Откладываем вычисленные значения продольной силы от горизонтальной оси

(«+» ‒ вверх, «-» ‒ вниз).

На участках с распределенной нагрузкой подсчитанные значения соединяем наклонными линиями, а на остальных усилие N не зависит от z и изображается горизонтальными линиями. Расставляем знаки, делаем штриховку. Убеждаемся в том, что «скачки» на графике по величине и направлению соответствуют внешним силам. Эпюра построена.

Когда стержень имеет опору только с одной стороны, усилия на участках можно определять, отбрасывая всегда ту часть стержня, к которой приложена неизвестная реакция. В этом случае неизвестная реакция никогда не потребуется для определения усилий, и эпюра может быть построена без определения реакций.

Например, в задаче 3.2 усилие на 5-м участке может быть получено суммированием правых сил:

N5= F3 + F2– F 1 -q2· 3 + q1· 2 = 20 + 10-40 - 5 ·3 + 30·2 = 35кН.

3.3Построение эпюр крутящих моментов при чистом кручении стержня

Кручением называется вид сопротивления, при котором в поперечных сече-

ниях стержня из шести возможных усилий возникает только одно - крутящий мо-

мент Mz (Mк).

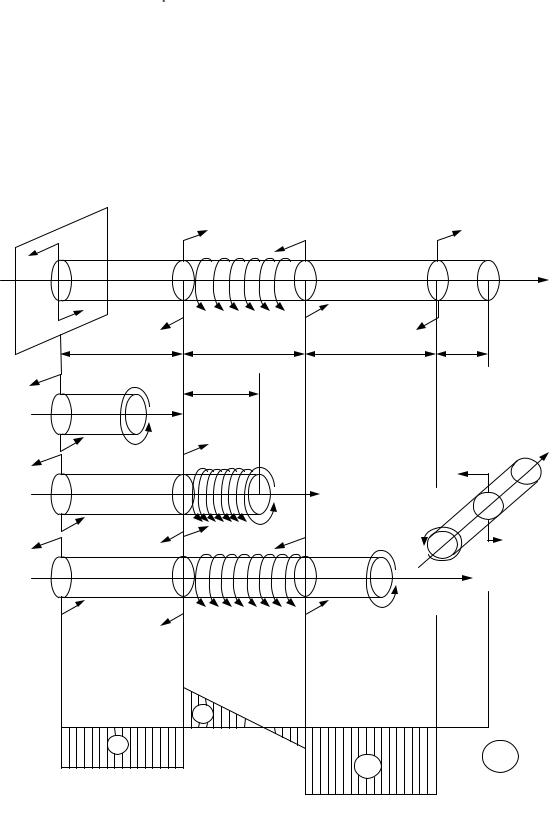
Задача 3.3. Построить эпюру крутящего момента Mz для стержня, изображенного на рис.

3.12 (для экономии места сам стержень и построения, выполненные в процессе решения,

показываются на одном рисунке).

Решение

Стержень загружен только моментами, действующими относительно оси z. Поэтому

в пространственной заделке А из шести возможных реакций не равна нулю только одна ‒

реактивный момент MA.

Найдем его из уравнения ∑ mz = 0.

MА =M1 -M2 -M3 +m·1,2=0

MА =M1 -M2 +M3 -m·1,2=8-5+7-5·1,2=4кНм.

Новым в данной задаче является наличие распределенной моментной нагрузки m=5

кНм/м, что означает, что на каждый метр длины участка действует распределенный

момент 5 кНм.

На участок длиной l=1,2 м в этом случае будет действовать равнодействующий

момент М = ml =51,2 = 6 кНм.

Поочередно рассекая каждый участок, будем, отбрасывая правую часть стержня, записы-

вать уравнение равновесия для левой: ∑ mz=0 , из которого будем определять величину

крутящего момента Mz (рис. 3.11). Его первоначальное направление будем считать на всех

участках положительным

1-й участок

MА+Mz=0; Mz=МА= -4 кНм = const.

Проводим горизонтальную прямую.

2-й участок

На участке приложен распределенный момент m, поэтому значение усилия Mz будет зависеть от расположения сечения. Рассматриваемое сечение свяжем с переменным расстоянием от края участка (можно от края стержня) z2, который изменяется в пределах от 0 (левый край участка) до 1,2 (правый край).

Итак , 0≤z2≤1,2м

Mz =-MA –M 1 +m· z2=0

Mz =-MA –M 1 +m ·z2=-4+8-5 z2=4-5 z2.

Строим прямую по двум точкам:

при z2 =0 Mz =4-5·0= 4 кНм, при z2 =1,2 Mz =4-5 1,2 =-2 кНм.

3-й участок

Mz +MA –M 1 +M2 +m·1,2=0 , откуда

Mz =-MA +M1 –M 2 -m·1,2= -4+8-5-5·1,2= -7кНм (на эпюре горизонтальная линия). Значение Mz несколько проще (рис. 3.12) определять из уравнения ∑ mz=0

Mz +M3=0 , откуда Mz =-M3=-7кНм.

4-й участок

Если взять сечение на 4-м участке, то очевидно, что правее него не приложено внешних сил, откуда ясно, что из уравнения ∑mz=0 следует MZ=0. Эпюра MZ построена

Рис. 3.12

3.4 ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ СИЛ В БАЛКАХ ПРИ ИЗГИБЕ

Балкой называется брус или стержень, работающий преимущественно на изгиб.

При этом нагрузки, действующие на балку, направлены перпендикулярно к оси стержня.

Если изгиб происходит в двух главных плоскостях (плоскостях, проходящих че-

рез главные центральные оси и ось z), то такой изгиб называют сложным.

Частный случай сложного изгиба, при котором нагрузка в вертикальной плоскости подобна (отличается множителем) нагрузке, приложенной в горизонтальной плоско-

сти, называется косым изгибом.

При сложном и косом изгибах в сечениях стержня возникают поперечные силы Qх,

Qу и изгибающие моменты Мx, My.

Если вся нагрузка, действующая на балку, приложена в вертикальной (или горизон-

тальной) плоскости, в сечениях возникает только два усилия: поперечная сила Qх и изги-

бающий момент Мy (или соответственно Qх и Мy ). Это прямой поперечный изгиб.

Рассмотрим подробное построение эпюр Qy и Мx при прямом поперечном изгибе.

При построении эпюр будем использовать правило знаков, а также зависимости Жу-

равского и выражение усилий через нагрузку.

Задача 3.4. Построить эпюры усилий Qy и Мх для балки, изображенной на рис. 3.13, ана-

литическим способом.

РИС. 3 . 1 3

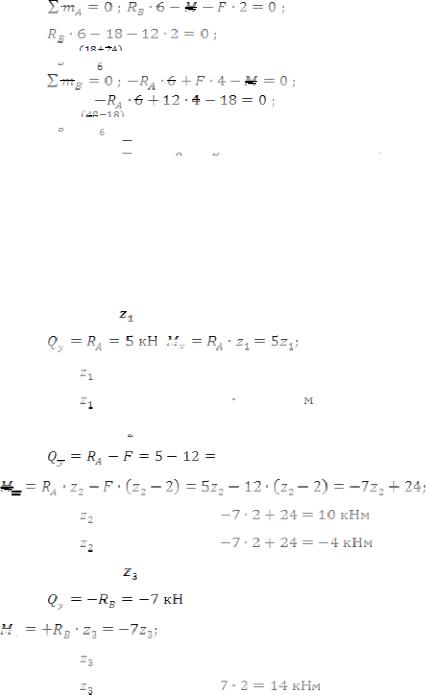
Решение

1.Определяем опорные реакции

= = 7 кН ;

= = 5 кН ;

Проверка: 2. Нумеруем участки. На каждом участке выбираем произвольное сечение, показы-

вая расстояние до него от левого или правого краев балки.

3. На каждом участке записываем аналитические выражения для Qy и Мх, рассмат-

ривая равновесие правой или левой частей балки.

Полученные функции изображаем графически на эпюрах.

2-й участок 2 ≤ ≤ 4 м

;

4. Эпюры Qy и Мх построены.

В рассмотренной задаче на балку воздействовали сосредоточенные нагрузки. В

следующей задаче демонстрируются основные приемы работы с равномерно-распреде-

ленными нагрузками.

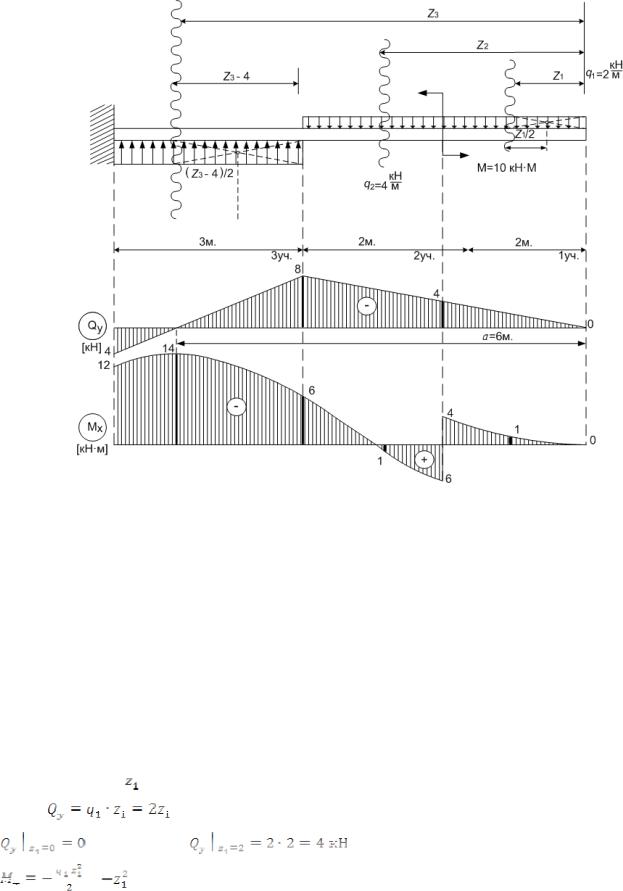
Задача 3.5. Построить эпюры поперечных сил и изгибающих моментов для балки, изо-

браженной на рис. 3.14.

Рис. 3.14

Решение

В данной балке можно построить эпюры, не определяя опорных реакций, если на всех участках выражения для Qy и Мх составлять, используя нагрузки, расположенные справа от сечения, а левую часть стержня (вместе с неизвестными реакциями) отбрасы-

вать.

Пронумеруем участки (по направлению). На каждом покажем произвольное сече-

ние, привязав его к правому краю балки.

Записываем аналитические выражения для Qy и Мх. Полученные функции изобра-

жаем графически.

; .

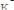
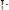
Выпуклость параболы – вниз.

Касательная к ней горизонтальна в сечении, где Qy = 0, то есть на краю балки.

При вычислении значений усилий необходимо указывать сечения, для которых про-

Еще один способ заключается в том, чтобы обозначить все сечения балки буква-

ми: A, B, C, D, E и т.д. В этом случае можно, например, записать

, что будет обозначать: «значение в сечении D».

Каждый вправе использовать тот способ указания сечений, который ему нравит-

ся.

2-й участок 2 м ≤ ≤ 4 м

Выпуклость параболы - вниз. Экстремумов нет.

На стыке 1-го и 2-го участков приложен сосредоточенный момент В силу этого на эпюре Мх образовался скачок, по величине и направлению совпадающий с внешним моментом.

3-й участок 4 м ≤ ≤ 7 м

Составляя выражения Qy() и Мх () заметим, что теперь справа от сечения оказа-

лась вся нагрузка q1 (равнодействующая q1 м с плечом () м) и часть нагрузки q2

(равнодействующая q2 ·() с плечом ()/2).

;