Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

9166

.pdf

Скачиваний:

Добавлен:

25.11.2023

Размер:

2.36 Mб

Скачать

☆

<<< < Предыдущая 12 / 72 3 4 5 6 7 > Следующая >>>

ренциальному уравнению L dIdt RI E . Найти зависимость силы тока I I t

от времени, если E меняется по закону E kt и I 0 0 ( L, R, k - постоянные),

k– коэффициент пропорциональности.

§5. Дифференциальные уравнения второго и высших порядков,

допускающие понижение порядка

В задачах 10.132 10.156 найти общее решение данных дифференци-альных уравнений.

10.132.	xy 1. 10.133. y cos 3x .												10.134. y									1		. 10.135. y					1	.
10.132.	xy 1. 10.133. y cos 3x .												10.134. y								sin 2			. 10.135. y						.
																					sin 2		x						x5
10.136.	y e4 x .				10.137. y ln x . 10.138.														xy		y .		10.139. x2 y y 2 .
						2									y					y						y y x
10.140.						1.		10.141.				y				1			ln			.	10.142.			y y x					.
10.140.	2xy y			y		1.		10.141.				y				1			ln			.	10.142.								.
															x					x
			y								2
10.143.	y		x x .				10.144. x					y		xy				1.				10.145.			xy	y	1 x . 10.146.
10.143.	y		x x .				10.144. x					y		xy				1.				10.145.			xy	y	1 x . 10.146.
xy	y 0 .					10.147. yy y 2 .															10.148.				y3 y 1.
10.149. yy y 2					1 0. 10.150.						1 y 2						2yy 0 . 10.151. 2 yy y 2 .
							.
10.152.	y					2		10.153.					y								2	.	10.154.					2 y . 10.155.
10.152.	y	y		1	( y )			10.153.					y				1 y					.	10.154.			3y y		2 y . 10.155.
								2		y		2
y y ln y .				10.156.			y							0 .
y y ln y .				10.156.			y		1 y					0 .

В задачах 10.157 10.173 найти соответствующие частные решения дифференциальных уравнений.

10.157.

x ,

y 0

0 ,

y 0 0 .

10.158. y

, y 1 2 ,

ln 2

y 1 1,

1 1.

10.159.

cos2

0 .

2 x

10.160. y e

y 0 8 ,

y 0 4 ,

y 0

2 . 10.161. 1 x

2xy

0 ,

y 0 0 ,

10.162.

y 1 0 ,

y 0 3 .

y 1 0 .

10.163.

1 y

0 ,

y 0 3 ,

10.164.

y e

y 0 2 .

x ln x y

y e 2 ,

e 4 .

10.165.

y 1 4 ,

y 1 0 .

10.166. tg x y y sin1 x 0 ,

y y ctg x sin 2x ,		π
	y
	y
		2

y 1 3 .

		π					π		1
y				0,			y			. 10.167.
y				0,			y			. 10.167.
		2					2		2
π					π						3	y 1 1 ,
	,					0 .		10.168. y			18 y ,

			y
2					2

		3	9 0 ,			y 1 1							3		y	4	16 ,	y 0 2
10.169.							,			10.170. y											2 ,
	y y							y 1 3 .			y
						2	y 1 y			y 0 2 ,
	2 .		10.171.						,											y
y 0						2 y						y		0 1. 10.172.
			3		y 0 0 ,													2	, y 0
18sin y cos y				0,				y 0 3 .		10.173.	y				tg y 2 y						2	,

y 0 1.

§6. Линейные дифференциальные уравнения второго

ивысших порядков с постоянными коэффициентами

Взадачах 10.174–10.186 составить линейное однородное дифферен-циальное уравнение с постоянными коэффициентами, фундаментальная система решений которого имеет вид.


10.174. e x , e 2 x		10.175.		e x , e x	10.176.	1, x .	10.177. ex , x ex .
10.178. sin 3x , cos 3x .			10.179. sin x , cos x, ex			.	10.180. e x , xe2 x , e2 x .
10.181. e x , e3x ,	1. 10.182. sin 2x, cos 2x,1. 10.183. 1, x , x 2 . 10.184. e x , e x ,
sin 2x, cos 2x .	10.185.		e x ,	xe x , sin x ,	cos x .	10.186. sin 3x, cos3x, 1, x .

В задачах 10.187–11.206 решить однородные линейные уравнения с постоянными коэффициентами.

10.187.	y 5 y 6 y 0 . 10.188. y 6 y 5 y 0 . 10.189. y 6 y 9 y 0 .
10.190.	y 6 y 0.	10.191.	y 9 y 0 .		10.192.	y 9 y 0 .
10.193.	y 6 y 10 y 0 .	10.194.	y y y 0 .		10.195.	4 y y 0 .
10.196. y 2 y 3y 0 .		10.197. y 2 y y 0 .			10.198. y 4 y
13y 0 . 10.199. y		y 0 . 10.200.		y y 0 .	10.201. y y 0 .
10.202.	y y 2 y 0 .	10.203.	y	y 0 . 10.204.		y y 0 .
10.205.	y y 0 .	10.206. y y 0 .

В задачах 10.207 – 10.215 найти частные решения уравнений, удовлет-воряющие указанным начальным условиям.

10.207.

5 y

6 y

0 ,

y 0

2 ,

10.208. y

4 y

4 y 0

y 0 1.

y 0 0 ,

10.209.

2 y

5 y

y 0 0 ,

y 0 2 .

y 0 1.

10.210.

y 0 3 ,

10.211.

9 y

0 ,

y 0 3 ,

y 0 2 .

10.212.

25 y 0

y 0 0 ,

10.213.

y 7 y

y 0 3.

0 1.

12 y 0 ,

y 0 4 ,

10.214.

8 y

16 y 0 ,

y 0 0 ,

0 3 .

10.215.

2 y

4 y 0 ,

y 0 1,

y 0 5 .

y 0 0 .

В задачах 10.216 10.235 найти общее решение неоднородного линей-ного уравнения, находя частное решение методом неопределённых коэффициентов.

10.216. y 3y 2 y 10e x . 10.217. y 2 y 2 y 2x . 10.218. y 4 y


5y 0 .		10.219. y 4 y 4 y xe2x .			10.220.		y 2 y y cos x .
10.221. y 3y 2e 3x .			10.222.	y 2 y 2 sin 3x .			10.223. y 4 y
2 cos 3x .		10.224.	y 3y 18x 9.			10.225. y 4 y x 2 1.
10.226.	y y cos x .		10.227. y y sin 2x .			10.228.		y 2 y 3y
e x cos x .		10.229. y 5y 8y 4 y e2x .				10.230.		y y 2x .
10.231.	y y 8e x .		10.232.	y y e x .		10.233.		y y 6x .
10.234.	y y 2xe x .		10.235.	y y cos x .

В задачах 10.236–10.248 найти частное решение неоднородного линей-ного уравнения, удовлетворяющие указанным начальным условиям.

10.236.	y 3y 2 y 2x 1,		y 0 0 ,		y 0 1.			10.237. y 4 y 3y
1 x ,	y 0 0 , y 0 2 . 10.238. y 5 y 6 y x 2							2 ,		y 0 0 ,	y 0 4 .
10.239.	y y 6 y x 2 ,		y 0 0 ,		y 0 3.			10.240. y 3y x 3 ,
y 0 0		10.241.		y	2 y x	2	1,		y 0 0 ,		y 0 4 .
	, y 0 3 .
10.242.	y y 4xe x ,	y 0 2 ,		y 0 0 .				10.243. y			y 4 sin x ,
y 0 1,	y 0 2 .	10.244.		y y sin 2x ,						y 1,	y 1.
					13


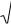
10.245. y 9 y 6 cos 3x ,		y 0 1,				y 0 3 .	10.246. y 2 y 3y
= 48x 2 e x ,	y 0 1, y 0		3	.	10.247. y y 2x , y 0 0 ,			y 0 1,

		2
y 0 2 . 10.248. y y 8e x ,					y 0 1, y 0 0 , y 0 1,			y 0 0 .

В задачах 10.249–10.260 найти общее решение методом вариации произвольных постоянных.

10.249.

y 4 y

10.250. y y tg x .

10.251.

y y ctg 2

x 0 .

sin 2x

10.252.

y 9 y

. 10.253. y 4 y

. 10.254. y 2 y y

cos 3x

sin 2 x

x 2

10.255. y y

10.256. y 2 y

. 10.257.

1 e x

y 2 y y

e x

10.258. y y

e x

10.259.

e x

ln x

6 y

9 y e3x .

10.260.

y y e2x

1 e2x .

В задачах 10.261–10.270 решить дифференциальные уравнения, приме-няя принцип суперпозиции решений.

10.261.	y 2 y y sin x e x .				10.262. y y 2e x x 2 .
10.263.	y 4 y 4 y sh x sin x .				10.264. y 4 y 4 y sin x cos 2x .
10.265. y y 6x e x .					10.266. y y xe x	cos x .
	y 25 y 3e x		4				e	2x
10.267.				.	10.268. y 4 y 13y x 2				.

		cos 5x
							cos 3x

10.269.	y y cos2 x x 2 .				10.270. y 4 y x sin 2 x .

В задачах 10.271 – 10.279 найти общие (частные) решения систем линейных дифференциальных уравнений с постоянными коэффициентами.

10.271.

10.273.

10.272.

x 3y,

x 5 y,

4x y,

10.274.

10.275.

10.276.

3x y.

x 3y.

18x y.


			dx
10.277.					3x 5 y,
			dt			x 0 2, y 0 5.
	dy			2x 8 y.

dt
dx				2x y sin t,
10.279.		dt					при условии
	dy			4x 2 y cos t

dt

dx y,

10.278. dt

x et e t .

x π 1, y π 2 .

Глава 11

ДВОЙНЫЕ ИНТЕГРАЛЫ

§ 1. Расстановка пределов интегрирования

В задачах 11.1 11.17 найти пределы двойных интегралов f x , y dxdy при дан-

ных (конечных) областях интегрирования D , представив интегралы в виде одного из повторных интегралов.

11.1.	D — прямоугольник со сторонами x 1, x 4 , y 0 , y 2 .
11.2.	D — прямоугольник :	0 x 2,	1 y 5 .
11.3.	D — треугольник со сторонами		x 0 , y 0 , x y 2 .
11.4.	D — треугольник :	x 3y 0 ,	y 2x 0 , x 3 .
11.5.	D — ограничена линиями x y 2, 4x 4 y 2 .

11.6. D :

11.9. D :

x 0,

0 y 1,x y 2 4.

x 0,

y x 3,x 2 y 2 .


1 x 2,		x 0,
11.7. D : y x,	11.8. D : y 0,
		2	y	2	1.
xy 1.	x		y		1.

11.10. D ограничена линиями							y x 3, y 2x 2 , x 0 .
11.11. D ограничена параболами							y x 2 ,	x y 2 .
	x 2			y 2				2	2
11.12. D :						1.	11.13. D : x 2 y 3			4 .
11.12. D :	4			9		1.	11.13. D : x 2 y 3			4 .
	4			9
	x 0,							x 0,5,
11.14. D : 4 y 3x,							11.15. D : y x,
		2	y		2	25.
	x		y			25.		xy 1.

11.16. D треугольник со сторонами y x , y 2x , x y 6 .
11.17. D параллелограмм: y x , y x 3, y 2x 1, y 2x 5 .
В задачах 11.18–11.25 представить двойные интегралы f x , y dxdy , где	D за-
D

данные ниже треугольники, в виде одного повторного интеграла, выбрав соответствующим образом порядок интегрирования.

11.18.				11.19.
		y			y
.				.
.				.
.				.
.				.
.				.
. .		. . .	x	. .	. . .		x
.				.
11.20.				11.21.
	. y			. y
.				.
.				.
. .		. . .	x	. .	. . .		x
.				.
.				.
.
11.22.				11.23.
.		y		.	y
	.			.
.				.
. . .		. . .	x	. . .	. .	.	x
.				.

11.24.		11.25.
	y		y
	.		.
	.		.
	.		.
. .	. . . x	. .	. . .	x
	.		.
	.		.

В задачах 11.26 – 11.35. представить двойные интегралы f x , y dxdy , где D -

заданные ниже области, границы которых составлены из отрезков прямых и дуги окружности, в виде одного повторного интеграла, выбрав со-ответствующим образом порядок интегрирования.

11.26.		y		11.27.	у
		.			.
		.			.
. .		. . . .	x	. .	. . .	x
		.			.
		.			.
11.28.		y		11.29	у	,
		.			.
		.			.
	. .	. . .	x	. .	. . .	x
		.			.

11.30.	y	11.31.		y .
	.			.
	.			.
. .	. . . x	.	.	. . .	x
	.			.
	.			.

11.32.		y		11.33.	. у
		.			.
		.			.
.	.		. . . x	. .	. . .	x
		.			.
		.			.
		.			.

11.34.			11.35.
		y		. у
		.		.
		.		.
	. .	. . . x	. .	.	. .	x
		. . . x	. .	.	. .	x
		.		.
		.		.	f x , y dxdy в виде сум-
		.		.
В задачах 11.36 – 11.43 представить двойной интеграл
					D

мы повторных интегралов (с наименьшим числом слагаемых), если граница области D составлена из отрезков прямых линий и дуг окружностей.

11.36.					11.37.
	y							y
	.						.
	.						.
	.						.
. . . . .			.	x	. . . . . .							x
	.						.
11.38.					11.39.
	y.							y
	.						.
	.						.
	.						.
	.						.
. .	. .		.	x	. .					. .		x
	.						.
11.40.					11.41.
	y							y
	.						.
	.						.
	.						.
. . . .		.	.	x	. . .				.	. .		x
11.42.					11.43.
	. y							y
	.						.
	.						.
	.						.
	.						.
. . . . .			.	x	.	. .			.		. .	x
	.						.
	.						.
В задачах 11.44 – 11.75			изменить порядок интегрирования.

3	3 x	0	x 1	0	0	x , y dx .
11.44. dx	f x, y dy .	11.45. dx	f x, y dy .	11.46. dy	f	x , y dx .
0	0	1	0	1	y 1

0	2 y 2		5	25 y 2
11.47. dy	f	x, y dx .	11.48. dy	f x, y dx . 11.49.
1	0		0	0

2	4
dx f x, y dy .
2	x 2

	1					x	f x, y dy .			1			y
1.50. dx							f x, y dy .	11.51. dy f x, y dx .
	0				x 2					0		y
	2					y 2			2		4
11.53. dy f x , y dx .								11.54. dy			f			x , y dx .
	0				0				0		y 2
	0						3 y 3			1			2 x
11.56.					dy		f x, y dx . 11.57.				dx				f x, y dy .
		1					2 y 2			2				x 2
			π
						cos x			2			2 x
	2					cos x			2			2 x			x , y dy .
11.59. dx							f x, y dy .	11.60.		dx			f		x , y dy .
	0					1 x			6			x	2	1
												x
												4
												4

1	1 x							4	25 y2
1	1 x				x , y dy . 11.63. dy					f x ,				y dx . 11.64.
dx		f			x , y dy . 11.63. dy					f x ,				y dx . 11.64.
0								0	0
0	1 x			2				0	0
	1 x

				2			cos x
11.52. dx f x, y dy .
			0			0
			1 2 2x					x,	y dy .
11.55.			dx				f	x,	y dy .
			0		2x 2

			1		1			x
11.58.			dx				f x, y dy .
			0				x 2

	1					1 x 2
11.61. dx								f x, y dy . 11.62.
	0				1	x 1 2
					2	x 1 2
					2
2		2 y
dy		f x, y dx .
6	1	y 2	1
	4	y 2	1
	4

		2	x
		2	x						1		2 y							0 2 1 y 2
11.65.		dx f x, y dy .					11.66.		dy		f ( x, y)dx .				11.67.			dy		f ( x, y)dx .
		1	1						2		y 2							1			y
			x
																		1
		4		25 x 2					2		2 y							1		2 y y 2
11.68.		dx			f ( x, y)dy .		11.69. dy					f ( x, y)dx .			11.70. 2dy						f ( x, y)dx . 11.71.
		0			3				0			4 y	2					0	1 1 y			2
					4 x
1	1 x						3	25 y 2							1	2 x
dx f (x, y)dy .						11.72.	dy	f ( x,			y)dx .			11.73.		dx		f x, y dy .
0	x 1						0	3	4						2	x	2
0	x 1						0	3									2

										1 y
		3		4 x					1	1 y
11.74.		dx		f ( x, y)dy .			11.75.		dy		f (x, y)dx .
		0	0						0		y 2

В задачах 11.76–11.77 изменив порядок интегрирования, записать данное выражение в виде одного повторного интеграла.

1	x	2	2 x
11.76. dx		f x, y dy + dx	f x, y dy .
0	0	1	0

			3 x
	x 2	3
1	x 2	3	2
11.77. dx		f x, y dy + dx	f x, y dy .
0	0	1	0

§ 2. Вычисление кратных интегралов

В задачах 11.78 – 11.95 вычислить повторные интегралы.

	4		2		4		x2				2		2 x
11.78.	dx x 2 ydy .				11.79. dx x y dy .				11.80.		dx		x 2 dy .
	1	0			0		0				2		0
						2 y2 1
	3		9 x2		1	2 y2 1		1 y 2 dx .		3	5
11.81.	dx			x y dy .	11.82. dy			1 y 2 dx .	11.83.	dy		x 2 y dx .
	0	0			0		y2			3	y2 4

					y 3		2		2 y
			1		y 3	xy2dx . 11.85.	2		2 y	x 2	y 2 dx .		0,5		y
11.84.			dy			xy2dx . 11.85.	dy			x 2	y 2 dx .	11.86. dy		4xy x dx 11.87.
			0		y		0		0				0	y
												π
	y2		y2				x2 1						2 y
2	y2	e	y2			1	x2 1					2	2 y
dy		e		dx .		11.88. dx		xe y dy .			11.89.	dy sin 2x 3y dx .
dy				dx .		11.88. dx		xe y dy .			11.89.	dy sin 2x 3y dx .
0	0		y			0	0					0	0
0	0					0	0					0	0

	1		4 x2			ln 4		1
11.90.	dx			xe3 y dy .		11.91.	dy 4 ye2xy dx .
	0			0		ln 3		0,5

		π
				2		0		0
	2			2		0		0		π xy
11.93.	dy 4 y 3 sin xy				2	dx .11.94. dy			y 2 cos	π xy
11.93.	dy 4 y 3 sin xy					dx .11.94. dy			y 2 cos	4
		π		1		1		2 y		4
		π		1		1		2 y

	4

11.92.dy 2 y 2e xy dx .

π2

dx .11.95. dy y cos xy dx .

π 1

В задачах 11.96 – 11.115 вычислить двойной интеграл

f x , y dxdy

по заданной

области

D в прямоугольных координатах, рационально выбрав порядок интегриро-

вания.

xdxdy ,

x2 y2

xydxdy ,

у x 2 ,

11.96.

где

D :

1.97.

где

D :

x y

y x.

y 2

y 2,

11.99. cos y

dxdy , где

x 0,

11.98.

dxdy ,

где

D : xy 1,

D :

x y,

D x

y x.

<<< < Предыдущая 12 / 72 3 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.11.20232.35 Mб09161.pdf
#
25.11.20232.35 Mб09162.pdf
#
25.11.20232.36 Mб09163.pdf
#
25.11.20232.36 Mб19164.pdf
#
25.11.20232.36 Mб09165.pdf
#
25.11.20232.36 Mб09166.pdf
#
25.11.20232.36 Mб09167.pdf
#
25.11.20232.36 Mб09168.pdf
#
25.11.20232.36 Mб09169.pdf
#
21.11.2023162.34 Кб0917.pdf
#
25.11.20232.36 Mб09170.pdf