
9018
.pdf
30
Решение. Подставив в уравнение прямой 3x y 1 0 координаты точки M 0 , то есть x0 1 и y0 2 вместо x и y , получаем: 3 1 2 1 3 1 2 0.
Следовательно, точка M 0 не лежит на данной прямой l .
Разным способам задания прямой соответствуют в прямоугольной систе-
ме координат разные виды ее уравнений.
Пусть на плоскости задана некоторая прямая l и декартова система координат.
1.Уравнение прямой, проходящей через заданную точку перпендику-
лярно данному вектору
Положение прямой l на плоскости однозначно определено, если задана неко-
торая точка M 0 (x0 , y0 ) , принадлежащая прямой l |
|
|
и некоторый вектор |
n A; B , |
|
перпендикулярный этой прямой (см. рис. 1). |
|
|
l |
y |
|
|
|
|
|
|
|
|
||
|
|
n |
|
|
|
|
M 0 (x0 |
; y0 ) |
|
|
|
|
0 |
. x |
Рис. 1 |
|
|
|
|
|
|
|
|
|
|
M (x; y) |
|
|
|
Возьмем на прямой произвольную точку |
M (x, y) и рассмотрим |
вектор |
|||
|
|
|
|
|
|
M 0 M x x0 ; y y0 |
(см. рис. 1). Так как векторы n и M 0 M |
перпендикулярны, |
|||
|
|
|
|
|
|
то их скалярное произведение равно нулю: n |
M 0 M 0 , то есть |
|
|||
|
|
A x x0 B y y0 0. |
|
(1) |
|
Уравнение (1) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.
Отметим, что вектор перпендикулярный данной прямой называется нормаль-
ным вектором этой прямой или вектором нормали.
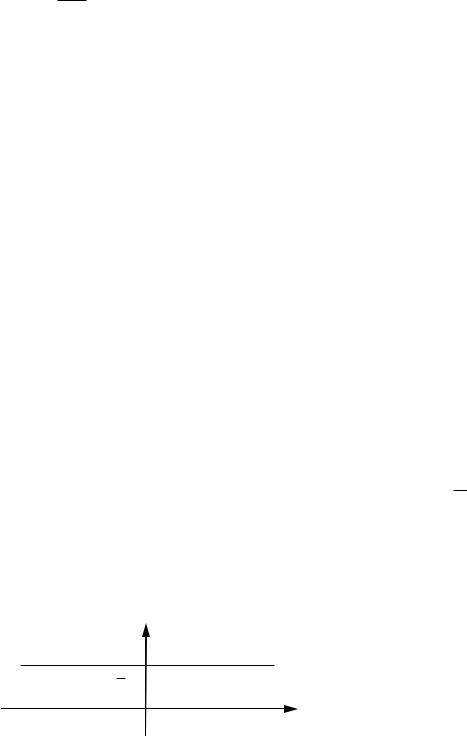
31
2. Общее уравнение прямой
Если в уравнении (1) раскрыть скобки и обозначить C Ax0 By0 , то полу-
чим общее уравнение прямой:
Ax By C 0. |
(2) |
Пример 2. Составить уравнение прямой l , проходящей через точку M 0 1; 2 и
перпендикулярной вектору PQ , если P 0;1 и Q 1; 2 .
|
|
|
|||
Решение. Находим координаты вектора PQ , являющегося вектором нормали |
|||||
прямой l : |
|
|
|
|
|
|
|
|
1 1;1 . |
||
n |
PQ 1 |
0; 2 |
|||
Подставляя в уравнение (1) координаты точки M 0 1; 2 , то есть x0 |
1, |
y0 2 |
||
|
1;1 , то есть |
A 1, B 1, находим искомое уравне- |
||
и координаты вектора n |
||||
ние прямой l : |
|
|
|
|
l : 1 x 1 1 y 2 0 или l : |
x 1 y 2 0 |
|
|
|
или l : x y 1 0 . |
|
|
|
|
Исследование общего уравнения прямой:
Выясним особенности расположения прямой по отношению к осям координат в зависимости от равенства (или неравенства) нулю тех или иных из чисел
A, B, C.
1) При A 0, B 0, C 0 уравнение (2) примет вид: By C 0 или y CB .
Это уравнение прямой на плоскости параллельной оси Ox и проходящей через
точку |
C |
. (См. рис. 2) |
|
0; |
|
|
|
|
B |
|
|
y
l
CB 0
0
Рис. 2

32
Пример 3. Построить прямую l : 3y 6 0.
Решение. Уравнение прямой l является общим уравнением прямой на плоско-
сти A 0, B 3, C 6, параллельной оси Ox и проходящей через точку 0; 2
(См. рис. 3).
y
0 x
l
-2
Рис. 3
2) При A 0, |
B 0, C 0 |
уравнение (2) примет вид: Ax C 0 |
или x |
C |
. |
|
|||||
|
|
|
|
A |
|
Это уравнение прямой на плоскости параллельной оси Oy и проходящей через
точку |
|
C |
|
. (См. рис. 4) |
|
|
|
; 0 |
|
A |
|
|||
|
|
|
|
y
|
|
C |
0 |
0 |
x |
|
A |
|
|
||
|
|
|
|
|
Рис. 4 |
3) При A 0 , |
B 0, C 0 уравнение (2) |
примет вид: Ax By 0 . Одним из ре- |
|||
шений уравнения является пара чисел x 0, y 0. Это означает, что прямая про-
ходит через начало координат. |
|
|
|
4) При A 0, B 0, C 0 |
уравнение (2) примет вид: |
By 0 или |
y 0 . Это |
уравнение координатной оси Ox . |
|
|
|
5) При A 0, B 0, C 0 |
уравнение (2) примет вид: |
Ax 0 или |
x 0. Это |
уравнение координатной оси Oy . |
|
|
|
3. Уравнение прямой в отрезках
Из (2) следует Ax By С и далее, предполагая, что C 0 (т.е. прямая не про-
ходит через начало координат) и, разделив обе части этого уравнения на C ,
получим уравнение

33
|
|
|
|
|
x |
|
y |
1, |
(3) |
|
|
|
|
|
|
a |
b |
||||
|
|
|
|
|
|
|
|
|||
в котором a |
C |
и b |
C |
величины отрезков, которые прямая |
«отрезает» от |
|||||
A |
A |
|||||||||
|
|
|
|
|
|
|
|
|||
осей координат (См. рис. 5). |
|
y |
l |
|
|
|
b |
a0 x
Рис. 5
Пример 4. Записать уравнение прямой l : 2x 3y 6 0 в отрезках и постро-
ить её.
Решение. Приведем заданное уравнение к уравнению вида (3).
2x 3 y 6 0 ; |
|
или |
|
2x 3 y 6 . |
||||||||
Разделив почленно последнее уравнение на 6 получим |
||||||||||||
|
2x |
|
3 y |
|
1; |
или |
x |
|
y |
1. |
||
|
|
|
|
2 |
||||||||
6 |
6 |
|
|
|
|
|
3 |
|
|
|||
Отметим на оси Ox точку x 3, а на оси Oy точку |
y 2 и через эти точки |
|||||||||||
проведем прямую. Это и будет искомая прямая (см. рис. 6). |
||||||||||||
|
|
|
y |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
x |
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
|
|
3 |
|
|
|||||
|
|
|
|
-2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
Рис. 6
Пример 5. Составить уравнение прямой l , проходящей через точку M 0 1; 2 и
отсекающей от осей координат равные отрезки.

34
Решение. Пусть уравнение искомой прямой l имеет вид (3). Так как a b по
условию, то |
уравнение (3) |
можно переписать |
в виде: |
|
x |
|
y |
или |
|||||
|
|
|
|
|
|||||||||
l : a |
a 1 |
||||||||||||
|
|
|
|
|
|
|
|
||||||
l : x y a . |
|
|
|
|
|
|
|
|
|
|
|
||
Поскольку точка |
M 0 1; 2 лежит на прямой l , |
то, подставляя ее координаты |
|||||||||||
x 1 |
y 2 |
в |
последнее |
уравнение, получаем |
a 3. Следовательно, |
||||||||
l : x y 3 – уравнение искомой прямой. |
|
|
|
|
|
|
|
|
|||||
4. |
Уравнение прямой с угловым коэффициентом |
|
|
|
|
|
|
|
|||||
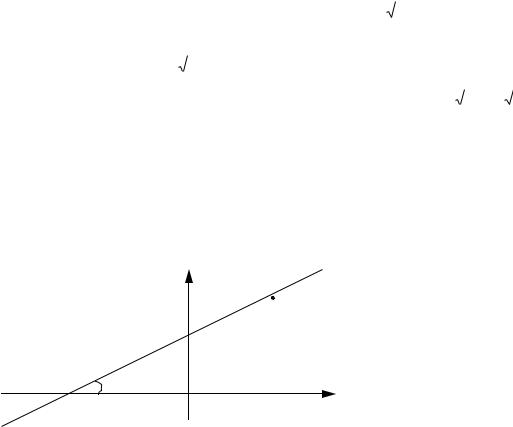
Пусть на плоскости Oxy задана произвольная прямая, не параллельная оси Oy.
Её положение однозначно определяется ординатой b точки N(0; b) пересечения с осью Oy и углом α между осью Ox и прямой (см. рис. 4).
Под углом ( 0 ) наклона прямой понимается наименьший угол,
на который нужно повернуть вокруг точки пересечения прямой и оси Ox про-
тив часовой стрелки ось Ox до ее совпадения с прямой.
Возьмем на прямой произвольную точку (см. рис. 7). Проведем
через точку N прямую параллельную оси Ox. Полученная точка P имеет коор-
динаты x и y b ,
|
|
y |
|
|
. M(x, y) |
||
|
|
y |
|
|
|||
|
|
|
|
|
|
|
|
|
N(0,b). |
. |
|
|
|||
|
|
P(x, y b) |
|||||
|
|
|
|
||||
|
|
|
|
||||
|
x |
|
|||||
0 |
|
|
x |
||||
|
|
|
|
||||
l |
|
|
|
||||
Рис.7
а угол между прямой NP и прямой l равен α. Из прямоугольного треугольника
NMP получаем равенство tg y b , т.е. y tg x b . Введя обозначение x
k tg , получаем уравнение |
|
y kx b, |
(4) |
35
которое называется уравнением прямой с угловым коэффициентом. Число k tg называется угловым коэффициентом прямой.
Пример 6. Составить уравнение прямой, отсекающей на оси ординат отрезок b 3 и образующей с положительным направлением оси абсцисс угол 6 .
Решение. Находим угловой |
коэффициент: |
k tg |
1 |
|
. |
Воспользовавшись |
||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
6 |
3 |
|
|
|
|
|
|
|
|
уравнением (4), получаем y |
1 |
|
x 3 . Освобождаясь от знаменателя и перенося |
|||||||||||
|
|
|
||||||||||||
3 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||||||||
все члены в левую часть, получаем общее уравнение прямой |
x 3 y 3 3 0 . |
|||||||||||||
5.Уравнение прямой, проходящей через данную точку в данном направлении
Пусть прямая l проходит через точку M 0 x0 ; y0 и ее направление характери-
зуется угловым коэффициентом k ( k tg ).
|
y |
|
|
|
M 0 (x0 ; y0 ) |
|
|
|
l |
0 |
x |
|
||
|
|
Рис.8 |
Тогда уравнение этой прямой можно записать в виде: l : y kx b , где b – по-
ка неизвестная величина. Так как точка лежит на прямой l , то ее
координаты удовлетворяют уравнению прямой l , то есть |
имеет место равен- |
|||||
ство: y0 k x0 b , откуда |
b y0 kx0 . Подставляя значение b в уравнение |
|||||
y kx b , получаем: y kx y |
0 |
kx |
0 |
или |
|
|
|
|
|
|
|
||
|
y y0 |
k x x0 |
(5) |
|||
Пример 7. Составить уравнение прямой l , проходящей через точку M 0 4; 5 и
образующей с положительным направлением оси Ox угол 45 .

36
Решение. По условию задачи x0 4, y0 5. Найдем угловой коэффициент
k tg 45 1. Подставив эти значения в уравнение (5) получим: |
y 5 (x 4) или |
x y 9 0. |
|
6. Каноническое уравнение прямой
Положение прямой на плоскости однозначно определено также и в том случае,
если задана некоторая точка M 0 x0 ; y0 на этой прямой и так называемый
|
|
|
|
|
|
|
|
|
|
|
|
|
направляющий вектор p m, n , параллельный данной прямой. |
||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
M 0 |
|
|
|
|
|
|||
|
|
l |
|
|
|
|
|
|
x |
Рис. 9 |
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
Возьмем |
на прямой |
произвольную |
точку M (x, y) и |
рассмотрим вектор |
||||||||
M 0 M x x0 ; y y0 . Так как векторы |
|
|
|
|
|
|
||||||
p и M 0 M |
коллинеарны, то имеем ра- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
венство |
M 0 M k p, |
где k |
- некоторое число. В координатах это равенство |
|||||||||
имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
x x0 k m |
y y0 k n, |
|
или |
|
|
x x0 |
|
k |
|
y y0 |
k. |
|
|
|
m |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
n |
||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x0 |
|
y y0 |
. |
|
|
(6) |
||
|
|
|
|
m |
|
|
|
|||||
|
|
|
|
|
n |
|
|
|
|
|
||
Полученное уравнение называется каноническим уравнением прямой на плос-
кости.
В частности, если одна из координат направляющего вектора равна нулю,
например, , то получаем уравнение прямой . p m, 0 y y0

37
Пример 8. Даны вершины треугольника: A 1; 2 , B 3; 1 и C 0; 4 . Составить уравнение прямой l , проходящей через вершину А треугольника и параллель-
ную стороне ВС.
Решение. Так ка по условию задачи прямая l параллельна стороне BC, значит
вектор |
|
|
|
|
|
|
|
|
|
|
|
|
||
BC является направляющим вектором этой прямой. Найдем координа- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ты |
вектора: |
|
BC |
0 |
3; 4 1 |
|
или |
BC 3; 5 . |
Подставляя в уравнение (6) координа- |
|||||
ты |
точки |
A |
и |
вектора |
|
|
|
|
|
|||||
BC , получаем каноническое уравнение прямой l : |
||||||||||||||
|
x ( 1) |
|
y 2 |
|
|
или |
x 1 |
|
y 2 |
. |
|
|||
|
|
|
|
|
|
|
|
|
||||||
|
3 |
5 |
|
|
|
|
|
3 |
5 |
|
|
|||
7. Уравнение прямой, проходящей через две заданные точки
Положение прямой на плоскости однозначно определено в том случае, если из-
вестны две точки M1 (x1 , y1 ) и M 2 (x2 , y2 ) , через которые проходит прямая.
y
 M 2
M 2
M1
l |
x |
|
Рис. 10 |
||
|
Нетрудно понять, что вектор M1M 2 x2 x1; y2 y1 можно считать направля-
ющим вектором данной прямой. Отсюда, используя уравнение (6), получим уравнение прямой, проходящей через две заданные точки
x x1 |
|
y y1 |
(7) |
|
x2 x1 |
|
y |
2 y1 |
|
|
|
|||
Пример 9. Составить уравнение прямой l , проходящей через точки M1 1; 2 и
M 2 1;3 .
38
Решение. Подставляя в уравнение (7) |
|
x1 1, |
y1 2 и |
x2 1, |
y2 3, полу- |
|||||||||||||||||||||
чим |
|
искомое уравнение прямой: |
|
y 2 |
|
|
x 1 |
или |
|
y 2 |
|
x 1 |
; |
т.е. |
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 2 |
|
1 1 |
|
|
|
1 |
|
2 |
|
||||
2 y 2 1 x 1 или 2y 4 x 1, следовательно, |
l : x 2y 5 0 . |
|
|
|
|
|||||||||||||||||||||
8. |
|
Параметрическое уравнение прямой |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
В уравнении (6) введем обозначение |
x x0 |
|
|
y y0 |
t, |
где t |
называется пара- |
|||||||||||||||||||
|
m |
|
n |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
метром ( t ), тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x x0 |
|
t |
x x |
|
|
mt |
x x |
|
|
mt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y y0 |
t |
y y |
|
nt |
y y |
|
nt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
x x0 |
m t |
t . |
|
|
|
(8) |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
y y0 |
n t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Это так называемые параметрические уравнения прямой. Ясно, что при изме-
нении значения параметра t в пределах от до точка M ( x, y) «пробега-
ет» всю прямую l . Очевидно, что точке M0 ( x0 , y0 ) соответствует значение па-
раметра t 0 .
Пример 10. Составить параметрическое уравнение прямой, проходящей через
точку |
|
|
|
|
|
|
M 1; 2 параллельно вектору a 3;5 . |
|
|
|
|
||
Решение. Подставляя в уравнение (8) координаты вектора |
|
и точки M, полу- |
||||
a |
||||||
чаем искомое параметрическое уравнение |
x 1 3t |
. |
|
|
||
|
|
|
|
|||
|
|
y 2 |
5t |
|
|
|

39
Взаимное расположение прямых на плоскости
1). Пусть две прямые l1 и l2 заданы уравнениями с угловыми коэффициентами k1 и k2 , соответственно, то есть l1 : y k1 x b1 ; l2 : y k2 x b2 . Требуется найти угол , на который надо повернуть в положительном направлении прямую l1 ,
вокруг точки их пересечения до совпадения с прямой l2 . (См. рис.11)
y |
|
|
l2 |
|
|
|
|
|
|
|
|
|
l1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
0 |
|
|
|
x |
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
Рис. 11 |
|
По теореме о внешнем угле треугольника, имеем: |
2 1 |
или 2 1 . |
|||||
Если 90 , то |
|
|
|
|
|
|
|
tg tg 2 |
1 |
|
tg 2 tg 1 |
. |
|
||
|
|
||||||
|
|
|
1 tg 1 tg 2 |
|
|||
Но так как tg 1 k1 и tg 2 k2 , то
tg |
k2 |
k1 |
(9) |
|
1 k1 k2 |
||||
|
||||
Таким образом, формула (9) позволяет находить угол между двумя прямыми на плоскости.
Пример 11. Найти угол между прямыми l1 : x 2 y 1 0 и l2 : 3x y 3 0 .
Решение. Запишем общее уравнение заданных прямых l1 и l2 в виде уравнений
с |
угловыми |
|
коэффициентами k |
и k2 , |
соответственно: |
l : 2 y x 1 или |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
l |
: y |
1 |
x |
1 |
|
, |
значит k |
1 |
; |
l2 : y 3x 3 , |
значит k2 3. |
Подставляя найден- |
|||||
|
|
||||||||||||||||
|
|
|
|
||||||||||||||
1 |
2 |
2 |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ные значения |
k |
1 |
и k |
|
3 |
в формулу (9), находим угол |
между прямыми l |
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и l2 :
