
9017
.pdf
10
Коллинеарные векторы могут быть направлены одинаково или противо-
положно. Нулевой вектор считается коллинеарным любому вектору.
|
|
|
Два вектора a |
и b |
равны, если они коллинеарны, одинаково направлены |
a b и их длины равны |
| a | | b |. Отсюда следует, что при перемещении векто- |
|
ра параллельно самому себе, получим равный ему вектор. Равные векторы назы-
вают также свободными.
Три вектора (или более трех) называются компланарными, если они ле-
жат в одной плоскости или в параллельных плоскостях. Если среди векторов
хотя бы один нулевой или два любые коллинеарны, то такие векторы компланар-
ны.
|
|
|
|
|
|
|
|
|
|
||||
|
|
На рис. 2 |
векторы a, b и c |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||
некомпланарны, |
так как векторы a |
|
|||||||||||
|
|
|
|
|
|
||||||||
и c параллельны плоскости АВС, а |
|
||||||||||||
|
|
|
|
||||||||||
вектор b не параллелен этой плоско- |
|
||||||||||||
сти, так как пересекает эту плоскость |
Рис. 2 |
||||||||||||
в точке В. |
|
|
|
|
|
|
|
|
|
||||
Под линейными операциями над векторами понимают операции сложе-
ния и вычитания векторов, а также умножение вектора на число.
Суммой двух векторов a и b называется третий вектор c , начало кото-
рого совпадает с началом вектора a , а конец – с концом вектора b ,
причем конец вектора a и начало вектора b совмещаются и обозначается:
c a b .
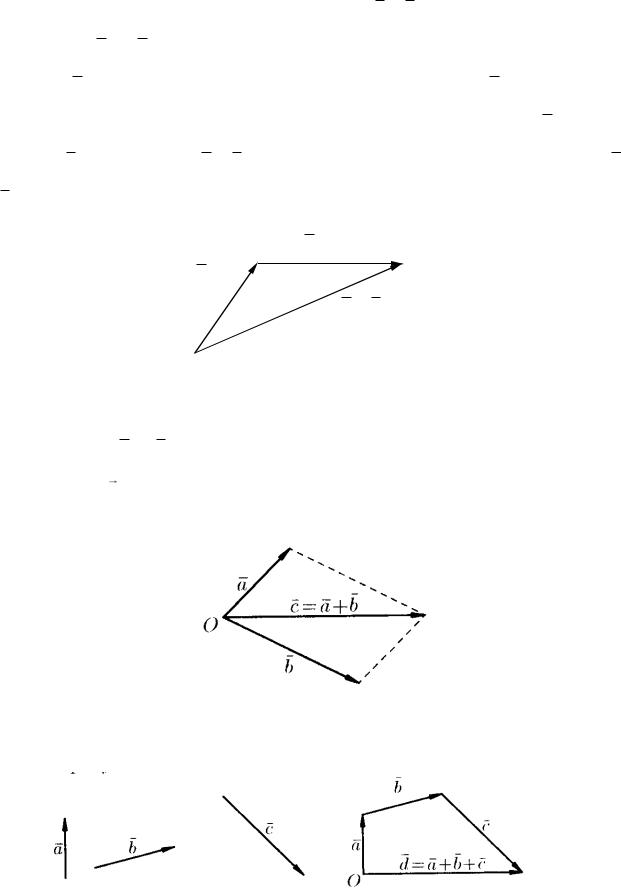
Пусть даны вектора a и b (см. рис. 3).
|
|
|
a |
b |
|
Рис.3
11
Чтобы их сложить, то есть найти сумму a b этих векторов, необходимо нарисовать a и b в одном и том же масштабе таким образом, чтобы начало вектора b – второго слагаемого, совпало с концом вектора a – первого слага-
емого (см. рис. 4). Тогда отрезок, соединяющий начало вектора a с концом вектора b будет суммой a b в том же масштабе, в котором представлены a и b . Такое правило сложения векторов называют правилом треугольника.
b
a
a b
Рис. 4
Существует еще одно правило сложения векторов - правило параллелограм-
ма: на векторах a и b , имеющих общее начало, строится параллелограмм, тогда
начало вектора c совпадает с общим началом векторов a и b , а конец – с про-
тивоположной вершиной параллелограмма (рис.5).
Рис. 5
На рис. 6 показано сложение трех векторов.
Рис. 6

12
Противоположным вектору a называется такой вектор
при сложении с вектором a дает нулевой вектор, то есть a a 0 .
Под разностью векторов a и b понимается вектор c a b такой, что a c b (см. рис.7).
Рис. 7
Можно вычитать векторы по правилу: a b a b , то есть вычита-
ние векторов заменить сложением вектора a с вектором, противоположным вектору b .
Отметим, что в параллелограмме, построенном на векторах a и b , одна направленная диагональ является суммой векторов a и b , а другая – разностью
(см. рис. 8).
Рис. 8
Произведением вектора a на число называется такой вектор a ,
направление которого совпадает с вектором a , если 0 и противоположно направлению вектора a , если 0; длина же вектора a в раз «больше»
длины вектора a , то есть
a a .
Если 0 , то a 0 .

13
Пусть дан вектор a (см. рис. 9), тогда векторы b 2a , c 3a изоб-
ражены на рисунке 9.
b
a
c
Рис. 9
Свойства линейных операций над векторами:
1.a b c a b c
2.a b b a
3.a 0 a
4.a a 0
5.a a
6.a b a b
7.a a a
8.1 a a , где , , , – действительные числа.
Теорема 1 (критерий коллинеарности) Два ненулевых вектора a и b
коллинеарны тогда и только тогда, когда найдется единственное число такое,
что b a .
Теорема 2 (о разложении вектора по двум неколлинеарным) Любой век-
тор c на плоскости может единственным образом быть разложен по двум не-
коллинеарным векторам a и b , то есть
14
c ! , R c a b .
Теорема 3 (критерий компланарности) Три вектора a , b и c компла-
нарны тогда и только тогда, когда хотя бы один из них можно разложить по двум остальным, то есть , R c a b .
Теорема 4 (о разложении вектора по трем некомпланарным) Любой век-
тор d пространства может единственным образом быть разложен по трем не-
компланарным векторам a , b и
d ! , , R d a b c .
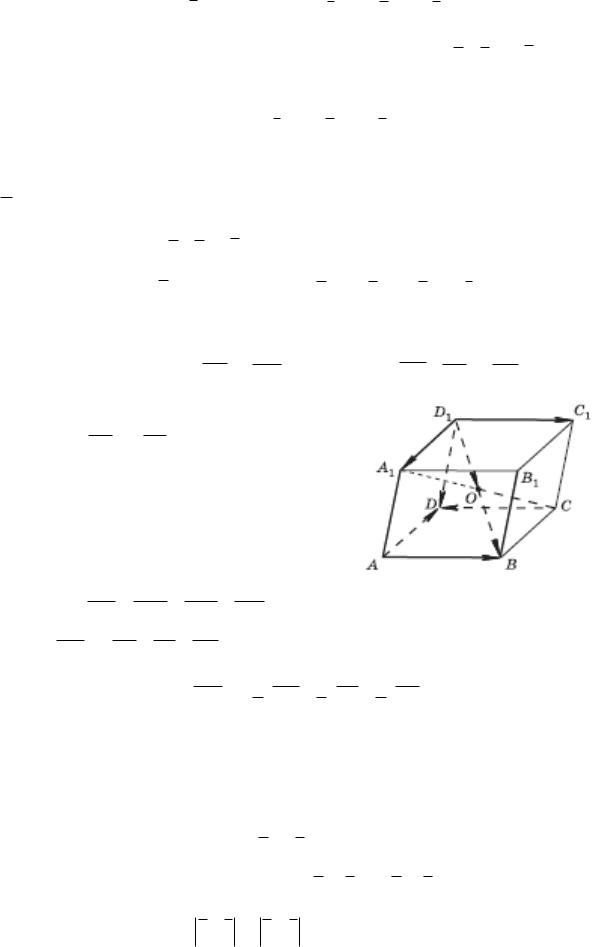
Пример. Диагонали параллелепипеда ABCDA1B1C1D1 пересекаются в точке О. Разложите векторы CD и D1O по векторам AA1 , AB и AD .
Решение.
1)Так как CD AB , то искомое раз-
ложение будет иметь вид:
|
|
|
|
|
|
|
|
|
|
|
||||
|
CD 0 AA1 1 AB 0 AD . |
|
||||||||||||
2) Заметим, что |
|
|
1 |
|
|
|
. В свою |
|||||||
D1O |
D1B |
|||||||||||||
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 10
очередь D1 B D1 A1 D1C1 D1 D
Или D1 B AD AB AA1 . Тогда получаем разложение :
D1O 12 AA1 12 AB 12 AD .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
Ответ: CD 0 AA1 1 AB 0 AD , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
D1O |
AA1 |
|
AB |
AD . |
|||||||||||||||||||||||||||||
2 |
2 |
2 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
13, |
|
|
|
19 , |
|
|
|
|
|
|
|
||||||||||||||
Пример. Найти |
a b |
, если |
a |
|
b |
a b |
24 . |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Поскольку векторы a и b ненулевые, то можно на них постро-
ить параллелограмм (см. рис. 8). Векторы a b и a b - направленные диа-
гонали параллелограмма, а a b и a b их длины. Из школьного курса гео-

15
метрии известно, что сумма квадратов диагоналей параллелограмма равна сумме квадратов сторон параллелограмма. Поэтому:
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
2 |
2 13 |
2 |
|
2 |
24 |
2 |
|
|
a b |
|
a b |
a |
|
b |
, отсюда |
a b |
19 |
484 , то есть |
||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a b 22 .
Ответ: a b 22 .
|
Задания для самостоятельной работы: |
|
||||
1) |
АВСДЕК – правильный шестиугольник, причем АВ х, |
ВС у . Выра- |
||||
|
зить через х, у и векторы СД , ДЕ, ЕК , КА, АС, АД , АЕ. |
|
||||
|
|
|
|
|
|
|
2) |
Даны неколлинеарные векторы a и b . Коллинеарны |
ли векторы |
||||
cа 2
 3b и d
3b и d 
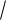 3а 6b ?
3а 6b ?
3)Точки K и L служат серединами сторон BC и CD параллелограмма
ABCD. Выразить векторы BC и DC через AK и AL .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4) Пусть векторы |
|
a |
и b неколлинеарны |
|
|
и |
|
AB |
a, BC4 a b, |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
CD 4 b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
и доказать коллинеар- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, DAa b. Найти числа |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
BC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ность векторов |
|
и DA . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
5) Какими должны быть векторы a и b , |
чтобы выполнялось неравенство |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
a |
b |
|
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6) Три силы |
|
|
F, F, F |
, приложенные к одной точке, |
имеют взаимно пер- |
||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
пендикулярные |
|
направления. Найти величину равнодействующей силы |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
2, |
|
F |
10, |
F |
11 |
||||||||
|
F , если известны величины этих сил: |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
2 |
|
3 |
. |
|
|
|||||||||||||||||||||||||||||||||||
§ 2. Проекция вектора на ось
|
|
|
|
|
|
|
|
|
16 |
|
|
|||
|
Пусть в |
пространстве |
задана |
|
|
ось l, |
|
|||||||
то |
есть |
направленная |
|
|
|
прямая. |
|
|||||||
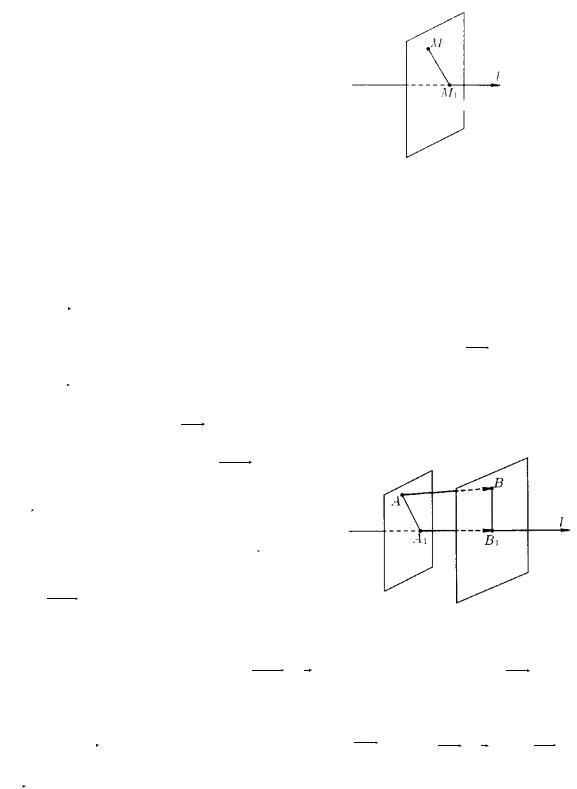
Проекцией точки М на ось l называется ос- |
|
|||||||||||||
нование M1 |
перпендикуляра MM1 , опущен- |
|
||||||||||||
ного из точки на ось. Точка M1 |
- это точка |
|
||||||||||||
пересечения |
оси |
l с плоскостью, |
|
|
|
|
Рис. 1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
проходящей через точку М перпендикулярно оси (см. рис.1). |
|
|||||||||||||
|
Если точка М лежит на оси l, то проекция точки М на ось l |
совпадает с |
||||||||||||
М. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
AB - произвольный ненулевой вектор. Обозначим через А1 и В1 |
||||||||||||
проекции на ось l |
соответственно начала |
А и конца В вектора AB и рассмот- |
||||||||||||
рим вектор A1B1 . |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Проекцией |
вектора |
AB |
|
на |
|
|
ось |
l |
|
||||
называется положительное число |
|
A1 B1 |
|
, если |
|
|||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||
вектор A1B1 |
и ось l одинаково направлены и |
|
||||||||||||
|
|
|
|
|||||||||||
отрицательное число, |
равное |
A1 B1 |
, ес- |
|
||||||||||
|
|
|
|
|
|
|
|
|||||||
ли |
вектор |
A1B1 |
и ось l |
противоположно |
|
|||||||||
направлены (см. рис. 2). |
|
|
|
|
|
|
|
|
Рис. 2 |
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
Если точки А1 и В1 |
совпадают ( A1B1 0 ), то проекция вектора AB равна |
||||||||||||
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проекция AB на ось l обозначается так: Пp l AB . Если AB 0 |
или АВ l, |
||||||||||||
то Пp l AB 0. |
|
|
|
|
|
|
|
|
|
|
|
|
||

17
Под углом между осью l и векто-
ром AB будем понимать меньший из углов,
который отсчитывается от направления оси до направления вектора (см. рис. 3). Очевидно,
Рис.3
что 0 .
Свойства проекции
1) Проекция вектора a на ось l равна произведению модуля вектора a
на косинус угла между вектором и осью, т.е.
|
|
|
|
|
|
|
Пp l a |
a |
|
cos . |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. |
|
|||||||||||||||||||||
а) Если 0 , то Пp l a |
|
a1 |
|
|
|
a |
|
cos |
(см. рис. 3) |
|||||||||||||
|
|
|
|
|||||||||||||||||||
б) Если |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
, то Пp l a |
a1 |
|
|
|||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
cos( ) |
|
a |
|
cos (см. рис. 4) |
|
||||||||||||||||
|
a |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) Если |
|
cos . |
|
|||||||||||||||||||
, то Пp l AB 0= |
a |
|
||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2)Проекция суммы векторов на одну и ту же ось равна сумме их проек-
ций на эту ось, т.е.
Пp l (a b) Пp l a Пp l b .
3)При умножении вектора a на число его проекция на ось также умножается на это число, т.е.
Пp l ( a) Пp l a .
Таким образом, линейные операции над векторами приводят к соответ-
ствующим линейным операциям над проекциями этих векторов.

18
§ 3. Координаты вектора и их свойства
Три единичных взаимно перпендикулярных вектора i , j , k простран-
ства, через которые условились выражать все векторы пространства, называют-
ся базисными векторами или базисом.
Прямоугольной декартовой системой координат в пространстве назы-
вается совокупность точки O и базиса i, j, k .
Точка O называется началом координат, оси Ox , Oy и Oz , проходящие
через начало координат – точку O в направлении базисных векторов i , j и k
называются осями координат. Плоскости xOy , xOz и yOz , проходящие через каждую пару осей координат называются координатными плоскостями.
Выберем произвольный вектор a
пространства и совместим его начало
с началом |
координат: |
a OM |
(см. рис. 1). |
Найдем проекции векто- |
|
ра a на координатные оси. |
Прове- |
|
дем через конец вектора OM плоско- |
||
сти, параллельные коорди- |
нат- |
|
Рис.1
ным плоскостям.
Точки пересечения этих плоскостей с осями обозначим соответственно
через M1 , M 2 , M 3 . Получим прямоугольный параллелепипед, одной из диа-
гоналей которого является вектор OM . По определению суммы векторов полу-
чае2м a OM OM1 M1 N NM . А так как M1 N OM 2 , NM OM 3 , то
a OM1 OM 2 OM 3 .
Заметим, что OM1 (Пp x a) i , OM 2 (Пp y a) j , OM 3 (Пp z a) k .

19
Обозначим через ax Пp x a , ay Пp y a , az Пp z a . Тогда a ax i ay j az k .
Эта формула является основной в векторном исчислении и называется
разложением вектора по ортам координатных осей. Числа ax , a y , az
называются координатами вектора a , то есть его координаты это проекции вектора на соответствующие координатные оси.
Векторное равенство a ax i ay j az k более кратко записывается a ax , ay , az .
Зная координаты вектора, можно легко найти его длину. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно записать
|
2 |
|
OM 2 |
|
2 |
|
OM 3 |
|
2 ax |
2 ay |
2 az |
2 . Отсюда |
|
| OM |2 |
OM1 |
|
|
|
|
||||||||
a 
 ax2 ay2 az2 .
ax2 ay2 az2 .
Пусть углы вектора a с осями |
Ох, Оу, Оz соответственно равны |
|||||||||||||||||||||
, , . По свойству проекции вектора на ось, имеем |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ax |
a |
cos , |
ay |
a |
cos , az |
a |
cos . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Или что то же самое, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
cos |
|
a |
x |
|
, cos |
ay |
, cos |
a |
z |
|
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
a |
|
|
a |
|
|
a |
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Числа cos , cos , cos |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
называются направляющими косинусами век- |
||||||||||||||||||||||
тора a . Направляющие косинусы обладают свойством |
|
|
|
|
|
|
||||||||||||||||
|
cos2 cos 2 cos 2 1 . |
|
|
|
|
|
|
|||||||||||||||
Итак, задав координаты вектора, всегда можно определить его модуль и направление, то есть сам вектор.
