
9013
.pdf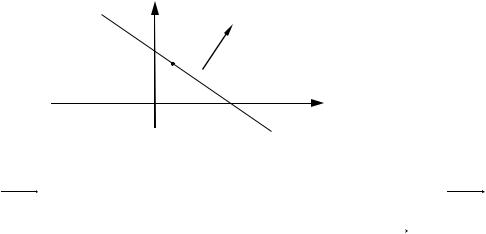
30
Решение. Подставив в уравнение прямой 3x y 1 0 координаты точки M 0 , то есть x0 1 и y0 2 вместо x и y , получаем: 3 1 2 1 3 1 2 0.
Следовательно, точка M 0 не лежит на данной прямой l .
Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды ее уравнений.
Пусть на плоскости задана некоторая прямая l и декартова система координат.
1.Уравнение прямой, проходящей через заданную точку перпендикулярно данному вектору
Положение |
прямой l на |
плоскости однозначно определено, если |
задана |
некоторая |
точка M 0 (x0 , y0 ) , |
принадлежащая прямой l и некоторый |
вектор |
|
|
|
|
n A; B , перпендикулярный этой прямой (см. рис. 1). |
|
||
l |
y |
|
|
|
|
|
|
|
|
||
|
|
n |
|
|
|
|
M 0 (x0 ; y0 ) |
. x |
|
|
|
|
0 |
Рис. 1 |
|
|
|
|
|
|
|
|
|
|
|
M (x; y) |
|
|
|
Возьмем на прямой |
произвольную точку |
M (x, y) и рассмотрим |
вектор |
||
|
|
|
|
|
|
M 0 M x x0 ; y y0 (см. рис. 1). Так как векторы n и M 0 M |
перпендикулярны, |
||||
|
|
|
|
|
|
то их скалярное произведение равно нулю: n |
M 0 M 0 , то есть |
|
|||
|
|
A x x0 B y y0 0. |
|
(1) |
|
Уравнение (1) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.
Отметим, что вектор перпендикулярный данной прямой называется
нормальным вектором этой прямой или вектором нормали.
2. Общее уравнение прямой

31 |
|
Если в уравнении (1) раскрыть скобки и обозначить |
C Ax0 By0 , то |
получим общее уравнение прямой: |
|
Ax By C 0. |
(2) |
Пример 2. Составить уравнение прямой l , проходящей через точку M 0 1; 2 и
перпендикулярной вектору PQ , если P 0;1 и Q 1; 2 .
Решение. Находим координаты вектора PQ , являющегося вектором нормали
прямой l : |
|
|
|
|
|
|
|
|
|
|
|
|
|
n PQ 1 0; 2 1 1;1 . |
|
|
|
|
||
Подставляя в уравнение (1) координаты точки M 0 1; 2 , то есть x0 |
1, |
y0 2 |
||||
|
|
1;1 , |
|
есть A 1, B 1, находим искомое |
||
и |
координаты вектора n |
то |
||||
уравнение прямой l : |
|
|
|
|
|
|
l : |
1 x 1 1 y 2 0 или |
l : |
x 1 y 2 0 |
|
|
|
или l : x y 1 0 . |
|
|
|
|
|
|
Исследование общего уравнения прямой:
Выясним особенности расположения прямой по отношению к осям координат в зависимости от равенства (или неравенства) нулю тех или иных из чисел
A, B, C.
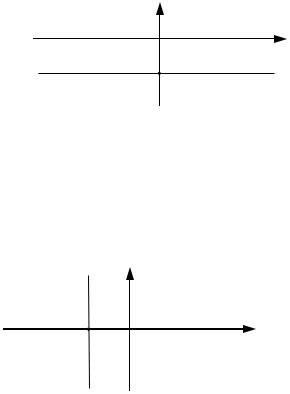
1) При A 0, B 0, C 0 уравнение (2) примет вид: By C 0 или y CB .
Это уравнение прямой на плоскости параллельной оси Ox и проходящей через
точку |
C |
. (См. рис. 2) |
|
0; |
|
|
|
|
|
||
|
B |
|
|
y
l
CB 0
0
Рис. 2
Пример 3. Построить прямую l : 3y 6 0.
32
Решение. Уравнение прямой l является общим уравнением прямой на плоскости A 0, B 3, C 6, параллельной оси Ox и проходящей через точку
0; 2 (См. рис. 3).
y
|
|
0 |
x |
|
|
|
|
l |
-2 |
|
|
|
|
|
|
Рис. 3 |
|
|
|
|
|
|
|
|
|
|
|
2) При A 0, |
B 0, C 0 уравнение (2) |
примет вид: Ax C 0 |
или x |
C |
. |
|
|
||||||
|
|
|
|
|
A |
|
Это уравнение прямой на плоскости параллельной оси Oy и проходящей через
точку |
|
C |
|
. (См. рис. 4) |
|
|
|
; 0 |
|
A |
|
|||
|
|
|
|
y
|
|
|
C |
0 |
|
|
x |
|
|
|||
|
|
|
A |
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Рис. 4 |
|
|
3) |
При A 0 , B 0, C 0 |
уравнение (2) примет вид: |
Ax By 0 . Одним из |
|||||||||
решений уравнения является пара чисел |
x 0, y 0. Это означает, |
что прямая |
||||||||||
проходит через начало координат. |
|
|
|
|
|
|
||||||
4) |
При A 0, B 0, C 0 |
уравнение (2) примет вид: |
By 0 или |
y 0 . Это |
||||||||
уравнение координатной оси Ox . |
|
|
|
|
|
|
||||||
5) |
При A 0, B 0, C 0 |
уравнение (2) примет вид: |
Ax 0 или |
x 0. Это |
||||||||
уравнение координатной оси Oy . |
|
|
|
|
|
|
||||||
|
3. Уравнение прямой в отрезках |
|
|
|
||||||||
Из |
(2) следует Ax By С и далее, |
предполагая, что |
C 0 (т.е. |
прямая не |
||||||||
проходит через начало координат) и, разделив обе части этого уравнения на C |
||||||||||||
, получим уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
y |
|
1, |
|
(3) |
|
|
|
|
|
a |
b |
|
|||||
|
|
|
|
|
|
|
|
|
||||

33
в котором a |
C |
и b |
C |
|
величины отрезков, которые прямая «отрезает» от |
|
A |
A |
|||||
|
|
|
||||
осей координат (См. рис. 5). |
|
|||||
y |
l |
|
|
|
b |
a0 |
x |
Пример 4. Записать уравнение прямой |
l : 2x 3y 6 0 в отрезках и |
|
Рис. 5 |
построить её.
Решение. Приведем заданное уравнение к уравнению вида (3).
2x 3 y 6 0 ; |
|
или |
|
2x 3 y 6 . |
||||||||
Разделив почленно последнее уравнение на 6 получим |
||||||||||||
|
2x |
|
3 y |
|
1; |
или |
x |
|
y |
1. |
||
|
|
|
|
2 |
||||||||
6 |
6 |
|
|
|
|
|
3 |
|
|
|||
Отметим на оси Ox точку x 3, а на оси Oy точку |
y 2 и через эти точки |
|||||||||||
проведем прямую. Это и будет искомая прямая (см. рис. 6). |
||||||||||||
|
|
|
y |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
x |
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
|
|
3 |
|
|
|||||
|
|
|
|
-2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
Рис. 6
Пример 5. Составить уравнение прямой l , проходящей через точку M 0 1; 2 и
отсекающей от осей координат равные отрезки.
Решение. Пусть уравнение искомой прямой l имеет вид (3). Так как a b по
условию, то уравнение (3) можно переписать в виде: |
|
x |
|
y |
или |
||
|
|
|
|
|
|||
l : a |
a 1 |
||||||
|
|
||||||
l : x y a . |
|
|
|
|
|
|
|

|
|
34 |
Поскольку точка |
M 0 1; 2 лежит на прямой l , то, подставляя ее координаты |
|
x 1 |
y 2 в |
последнее уравнение, получаем a 3. Следовательно, |
l : x y 3 – уравнение искомой прямой.
4. Уравнение прямой с угловым коэффициентом
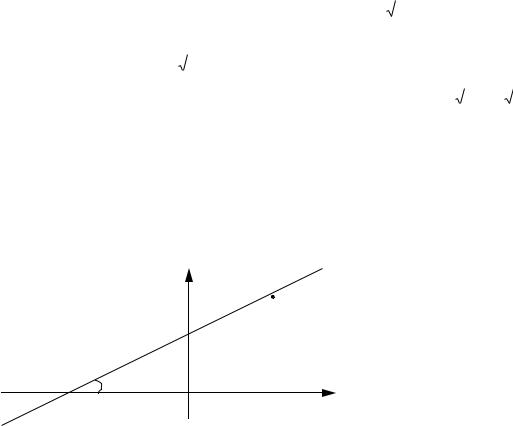
Пусть на плоскости Oxy задана произвольная прямая, не параллельная оси Oy.
Её положение однозначно определяется ординатой b точки N(0; b) пересечения с осью Oy и углом α между осью Ox и прямой (см. рис. 4).
Под углом ( 0 ) наклона прямой понимается наименьший угол,
на который нужно повернуть вокруг точки пересечения прямой и оси Ox
против часовой стрелки ось Ox до ее совпадения с прямой.
Возьмем на прямой произвольную точку (см. рис. 7). Проведем
через точку N прямую параллельную оси Ox. Полученная точка P имеет координаты x и y b ,
|
|
y |
|
|
|
|
. M(x, y) |
|||
|
N |
y |
|
). |
|
|
||||
|
|
|
|
|
|
|
||||
|
(0,b |
|
. |
|
|
|
||||
|
|
|
|
|
P(x, y b) |
|
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
|
x |
|
|
|||||
0 |
|
|
|
|
x |
|||||
|
|
|
|
|
|
|||||
l |
|
|
|
|
|
|
||||
а угол между прямой NP и прямой l равен α. Из прямоугольного треугольника |
||||||||||
|
|
|
|
|
|
|
|
|
Рис.7 |
|
NMP получаем равенство tg |
y b |
, |
т.е. y tg x b . Введя обозначение |
|||||||
|
||||||||||
|
|
|
|
|
x |
|
|
|
|
|
k tg , получаем уравнение |
|
|
|
|
|
|
||||
|
|
y kx b, |
|
|
(4) |
|||||
которое называется уравнением прямой с угловым коэффициентом. Число k tg называется угловым коэффициентом прямой.
Пример 6. Составить уравнение прямой, отсекающей на оси ординат отрезок b 3 и образующей с положительным направлением оси абсцисс угол 6 .
35
Решение. Находим угловой |
коэффициент: |
k tg |
1 |
|
. |
Воспользовавшись |
||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
6 |
3 |
|
|
|
|
|
|
|
|
уравнением (4), получаем y |
1 |
|
x 3 . Освобождаясь от знаменателя и перенося |
|||||||||||
|
|
|
||||||||||||
3 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||||||||
все члены в левую часть, получаем общее уравнение прямой |
x 3 y 3 3 0 . |
|||||||||||||
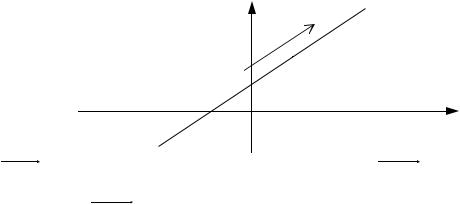
5.Уравнение прямой, проходящей через данную точку в данном направлении
Пусть прямая l проходит через точку |
M 0 x0 ; y0 и ее направление |
|
характеризуется угловым коэффициентом k |
( k tg ). |
|
|
y |
|
|
M 0 (x0 ; y0 ) |
|
|
|
|
l |
0 |
x |
|
||
Тогда уравнение этой прямой можно записать в виде: l : y kx b , где |
b – |
||||||
|
|
|
|
|
Рис.8 |
|
|
пока неизвестная величина. Так как точка M 0 x0 ; y0 лежит на прямой l , |
то ее |
||||||
координаты |
удовлетворяют уравнению прямой |
l , то есть |
имеет место |
||||
равенство: |
y0 k x0 b , откуда |
b y0 |
kx0 . |
Подставляя |
значение |
b в |
|
уравнение y kx b , получаем: y kx y |
|
kx |
или |
|
|
||
|
|
|
0 |
0 |
|
|
|
|
y y0 |
k x x0 |
|
|
(5) |
||
Пример 7. Составить уравнение прямой l , проходящей через точку M 0 4; 5 и
образующей с положительным направлением оси |
Ox угол 45 . |
|
Решение. По условию задачи x0 4, |
y0 5. Найдем угловой коэффициент |
|
k tg 45 1. Подставив эти значения в уравнение |
(5) получим: y 5 (x 4) или |
|
x y 9 0. |
|
|
6. Каноническое уравнение прямой |
|
|
36
Положение прямой на плоскости однозначно определено также и в том случае,
если задана некоторая точка M 0 x0 ; y0 на этой прямой и так называемый
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
направляющий вектор p m, n , параллельный данной прямой. |
||||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|||
|
|
|
|
p |
|
|
|
|
|
|
|
|||
|
|
|
|
|
M 0 |
|
|
|
|
|
|
|
||
Возьмем на |
прямой |
произвольную точку |
M (x, y)x и |
рассмотрим вектор |
||||||||||
|
|
|
l |
|
|
|
|
|
|
|
|
Рис. 9 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
M 0 M x x0 ; y y0 . |
|
|
|
|
|
|
|
|
|
|
|
|||
Так как векторы p |
и |
M 0 M коллинеарны, то имеем |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равенство |
M |
0 M k p, где k |
- некоторое число. В координатах это равенство |
|||||||||||
имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x0 k m |
|
y y0 k n, |
|
или |
|
x x0 |
k |
|
y y0 |
k. |
||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
m |
|
|
|
n |
|
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x0 |
|
y y0 |
. |
|
|
(6) |
|||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
m |
n |
|
|
|
|
|
|
||
Полученное уравнение называется каноническим уравнением прямой на |
||||||||||||||
плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В частности, |
если одна из координат направляющего |
вектора равна нулю, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
y y0 . |
|
|
|
|
например, |
p m, 0 , то получаем уравнение прямой |
|
|
|
||||||||||
Пример 8. Даны вершины треугольника: |
A 1; 2 , |
|
B 3; 1 и C 0; 4 . Составить |
|||||||||||
уравнение прямой l , проходящей через вершину А треугольника и параллельную стороне ВС.
Решение. Так ка по условию задачи прямая l параллельна стороне BC, значит
вектор |
|
|
|
|
|
|
|
BC |
является |
|
направляющим |
вектором этой прямой. Найдем |
|||
|
|
вектора: |
|
0 3; 4 1 или |
|
3; 5 . |
Подставляя в уравнение (6) |
координаты |
BC |
BC |
|||||

37
координаты точки A и вектора BC ,
получаем каноническое уравнение прямой l
: |
x ( 1) |
|
y 2 |
или |
x 1 |
|
y 2 |
. |
||
3 |
5 |
3 |
|
5 |
||||||
|
|
|
|
|
||||||
7. Уравнение прямой, проходящей через две заданные точки
Положение прямой на плоскости однозначно определено в том случае, если известны две точки M1 (x1 , y1 ) и M 2 (x2 , y2 ) , через которые проходит прямая.
y
 M 2
M 2
M1
l |
M |
M |
|
x |
|
x ; y |
x |
|
можно считать |
|
Нетрудно понять, что вектор |
2 |
2 |
2 |
y |
||||||
|
1 |
|
|
1 |
1 |
|
Рис. 10 |
|||
направляющим вектором данной прямой. Отсюда, используя уравнение (6),
получим уравнение прямой, проходящей через две заданные точки
x x1 |
|
y y1 |
(7) |
|
x2 x1 |
|
y |
2 y1 |
|
|
|
|||
Пример 9. Составить уравнение прямой l , проходящей через точки M1 1; 2 и
M 2 1;3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Подставляя в уравнение (7) |
|
x1 1, |
y1 |
2 и |
|
x2 1, |
y2 |
3, |
|||||||||||||||||
получим |
искомое |
|
уравнение |
прямой: |
y 2 |
|
x 1 |
или |
|
y 2 |
|
x 1 |
; |
т.е. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 2 |
1 1 |
|
|
1 |
|
|
2 |
|
|
||||||
2 y 2 1 x 1 или 2y 4 x 1, следовательно, |
l : x 2y 5 0 . |
|
|
|
|
||||||||||||||||||||
|
8. Параметрическое уравнение прямой |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
В уравнении (6) |
введем обозначение |
|
x x0 |
|
|
y y0 |
t, |
где t |
|
называется |
|||||||||||||||
|
m |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||||
параметром ( t ), тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x x0 |
t |
x x |
|
mt |
x x |
|
mt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
38 |
|
|
|
y y0 |
t |
y y |
|
nt |
y y |
|
nt |
|
|
|
|
|
0 |
0 |
|
|
||||||
|
n |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
Отсюда получаем: |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x x0 |
m t |
t . |
(8) |
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
y y0 |
n t |
|
|
||
Это так называемые параметрические уравнения прямой. Ясно, что при изменении значения параметра t в пределах от до точка M ( x, y)
«пробегает» всю прямую l . Очевидно, что точке M0 ( x0 , y0 ) соответствует значение параметра t 0 .
Пример 10. Составить параметрическое уравнение прямой, проходящей через
|
|
|
|
|
|
точку M 1; 2 параллельно вектору a 3;5 . |
|
|
|
|
|
Решение. Подставляя в уравнение (8) координаты вектора |
|
и точки M, |
|||
a |
|||||
получаем искомое параметрическое уравнение |
x 1 3t |
. |
|
|
|
|
|
|
|
||
|
y 2 |
5t |
|
|
|
Взаимное расположение прямых на плоскости
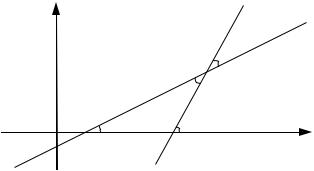
1). Пусть две прямые l1 и l2 заданы уравнениями с угловыми коэффициентами k1 и k2 , соответственно, то есть l1 : y k1 x b1 ; l2 : y k2 x b2 . Требуется найти угол , на который надо повернуть в положительном направлении прямую l1 ,
вокруг точки их пересечения до совпадения с прямой l2 . (См. рис.11)
39
y |
|
|
l |
2 |
|
||
|
|
|
|
|
l1 |
||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
||
0 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
По теореме о внешнем угле треугольника, имеем: 2 |
1 |
||||||
Если 90 , то |
|
|
|
|
|
|
|
tg tg 2 1 |
tg 2 tg 1 |
. |
|
||||
|
|
|
|||||
|
|
|
1 tg 1 tg 2 |
|
|||
Но так как tg 1 k1 и tg 2 k2 , то |
|
|
|
|
|
|
|
tg |
|
k2 k1 |
|
|
|
||
|
|
|
|
|
|
|
|
1 |
k1 k2 |
|
|
|
|||
Рис. 11
или 2 1 .
(9)
Таким образом, формула (9) позволяет находить угол между двумя прямыми на плоскости.
Пример 11. Найти угол между прямыми l1 : x 2 y 1 0 и l2 : 3x y 3 0 .
Решение. Запишем общее уравнение заданных прямых l1 |
и l2 |
в виде уравнений |
||||||||||||||||||||||||
с |
угловыми |
коэффициентами |
k |
и k2 , соответственно: |
l : 2 y x 1 или |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
l |
: y |
1 |
x |
1 |
, |
значит |
k |
|
1 |
; |
l2 : y 3x 3 , значит |
k2 3. Подставляя |
||||||||||||||
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
найденные значения |
k |
|
1 |
и k2 |
3 в формулу (9), находим угол между |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
прямыми l1 |
|
и l2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
3 |
1 |
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
7 , откуда |
arctg 7 . |
|
|
||||||||||||||
tg |
|
2 |
|
|
2 |
|
|
|
|
|||||||||||||||||
|
|
1 |
3 |
|
1 |
|
|
|
||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что если требуется вычислить острый угол между прямыми, то правая часть формулы (9) берется по модулю, то есть
tg |
k2 k1 |
. |
|
1 k1 k2 |
|
||
