Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

8989

.pdf

Скачиваний:

Добавлен:

25.11.2023

Размер:

2.12 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

5.Интегральное исчисление

5.1.Неопределенный интеграл

5.1.1. Правила интегрирования

f (x)dx F(x) C F

F(x) – первообразная функция от

f (x).

(x) f (x) ,

af (x)dx a f (x)dx.

x (t) – замена переменной.

f (x)dx f ( (t)) (t)dt

udv uv vdu – формула интегрирования по частям.

Pk (x)

(k l).

Q (x)

Если Q(x) (x a)m (x2

px q)n ,

то

P(x)

(x a)m

(x a)m 1

Q(x)

x a

B1x C1

B2x C2

Bnx Cn

(x2 px q)n

(x2 px q)n 1

x2 px q

R(sin x,cosx)dx:

sin x

cosx

1 t2

2dt

1 t

R(sin2 x,cos2 x)dx:

tgx t, sin2

, cos2

1 t

5.1.2. Таблица интегралов

dx x C

xndx	xn 1	C	(n 1)

	n 1

dxx ln x C

1 x2 arctgx C

	dx	arcsinx C


1 x2

exdx ex C

axdx ax C lna

chdx2 xdx thx C

shdx2 x dx cthx C

dx ln x a C x a

arctg

x a

a x

arcsin

a2 x2

sinxdx cosx C

x2 a2

cosxdx sinx C

sinx

sec2 xdx tgx C

cosx

cosec2xdx -ctgx C

tgxdx ln

cosx

shxdx chx C

ctgxdx ln

sinx

chxdx shx C

5.2. Определенный интеграл

5.2.1. Правила интегрирования

f (x)dx F(x) ba F(b) F(a) – формула Ньютона-Лейбница.

b b

udv uvba vdu – формула интегрирования по частям.

bt2

f(x)dx				( (t1) a, (t2) b) – замена переменной.
f(x)dx		f( (t)) (t)dt		( (t1) a, (t2) b) – замена переменной.
a		t1
	Несобственные интегралы
		b		b		b
	f ( x) dx	lim f ( x) dx ,			f (x) dx lim	f ( x) dx .
a		b			a	a
a		a			b	a	c α	b
					b		c α	b
Если на a c b и			f (c) ,		то f(x)dx	lim	f(x)dx	lim f(x)dx.
					a	α 0	a	β 0 c β

Несобственный интеграл сходится, если соответствующий предел существует и конечен. Несобственный интеграл расходится, если соответствующий предел не существует или бесконечен.

5.2.2. Приложения определенного интеграла

Площадь фигуры

b	b		t2
S f ( x) dx ,	S f2 ( x) f1( x) dx ,	S	f ( (t)) (t) dt
a	a		t1

S 1 ρ2 d .

2 α

Площадь эллипса

1 равна

S ab.

Длина дуги

1 y 2 dx,

x 2 y 2 dt,

ρ2 ρ 2 d .

Объем тела

V S(x)dx, где S(x) – площадь поперечного сечения.

Объем эллипсоида

1 равен

abc.

Объем тела вращения

y2 dx (вокруг оси Ox),

Vy x2 dy (вокруг оси Oy).

Площадь поверхности вращения

2 y

1 y 2 dx, (вокруг оси Ox),

Sy 2 x 1 x 2 dy

(вокруг оси Oy).

Пусть γ γ(x) – функция плотности распределения вещества по пло-

ской дуге y f (x). Для однородной дуги γ const.

Масса дуги M γ

1 y 2

dx.

Статические моменты и моменты инерции плоской дуги

dx ,

M x γ y

1 y 2

M y γ x

1 y 2

Ix γ y2

1 y 2

dx,

Iy γ x2

1 y 2

dx,

I0 Ix Iy.

Центр тяжести плоской дуги

M y

γ x

1 y 2

M x

γ y

1 y 2

1 y 2 dx

γ 1 y 2 dx

Пусть γ γ(x) – функция плотности распределения вещества по пло-

ской фигуре, ограниченной линиями

y 0, x a, x b,

y f (x). Для од-

нородной фигуры γ const.

Масса фигуры M γ ydx.

Статические моменты и моменты инерции плоской фигуры

	1	b	b
M x	1	γ y2 dx ,	M y γ xydx ,
M x	2	γ y2 dx ,	M y γ xydx ,
		a	a

	1	b	b
Ix	1	γ y3 dx ,	I y γ x2 y dx , I0 Ix Iy.
Ix	3	γ y3 dx ,	I y γ x2 y dx , I0 Ix Iy.
		a	a

Центр тяжести плоской фигуры

γ xy dx

γ y2 dx

M y

M x

2 a

M b

γ y dx

5.3. Двойной и тройной интегралы

5.3.1. Двойной интеграл

y2 (x)

x2 ( y)

V f (x, y)dxdy

f (x, y)dy

f (x, y)dx –

y1 (x)

x1 ( y)

объем (мера) цилиндрического тела, в основании которого лежит областьD , ограниченного поверхностью z f (x,y).

S dxdy – площадь (мера) области D .

f (x,y)dxdy f (ρcos ,ρsin )ρdρd –

объем цилиндрического тела в полярной системе координат.

S dxdy ρdρd – площадь в полярной системе координат.

z 2

пов

dxdy –

площадь поверхности, заданной уравнением z f (x,y);

D – проекция поверхности на плоскость xOy. Масса плоской пластинки D с поверхностной плотностью γ(x,y)

M γ(x,y)dxdy.

Статические моменты пластинки D относительно осей координат Mx y γ(x,y)dxdy – относительно оси Ox,

M y	x γ(x,y)dxdy – относительно оси Oy.
		D
xc		My	,	yc		M	x	– координаты центра тяжести пластинки		D .
xc		M	,	yc				– координаты центра тяжести пластинки		D .
		M				M
В случае однородной пластинки (γ(x,y) – константа):
		xdxdy						ydxdy	.
xc		D			,	yc		D
xc					,	yc		dxdy
		dxdy						dxdy
		D						D

Моменты инерции пластинки D

Ix y2	γ(x,y)dxdy – относительно оси Ox,
D
Iy x2	γ(x,y)dxdy – относительно оси Oy,

IO x2 y2 γ(x,y)dxdy – относительно начала координат.

5.3.2. Тройной интеграл

b y2 (x) z2 (x,y)

f (x,y,z)dxdydz dx				dy	f (x,y,z)dz – тройной интеграл по
	T	a		y1(x) z1(x,y)
области T {(x;y;z)			a x b, y1(x) y y2(x), z1(x,y) z z2(x,y)}.
области T {(x;y;z)			a x b, y1(x) y y2(x), z1(x,y) z z2(x,y)}.
V dxdydz – объем (мера) области T .
	T
f (x,y,z)dxdydz f (ρcos ,ρsin ,z)ρdρd dz –
	T	T		тройной интеграл в цилиндрических координатах.
				тройной интеграл в цилиндрических координатах.
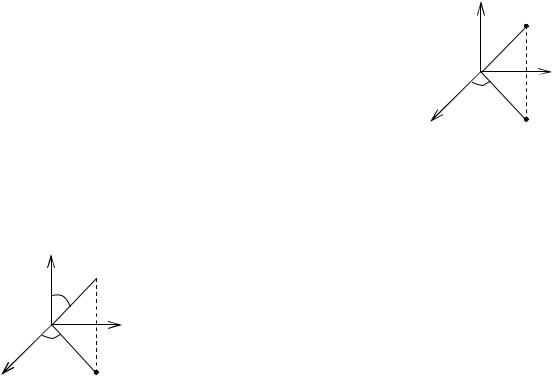
						z
x ρcos ,		– связь декартовых координат				M(x,y,z)
x ρcos ,		– связь декартовых координат				M( , ,z)
		(x;y;z) с цилиндрическими ко-				z
y ρsin ,		(x;y;z) с цилиндрическими ко-				z
	z z	ординатами (ρ; ;z) (рис. 5.1).				y
	z z	ординатами (ρ; ;z) (рис. 5.1).				y


						x
						Рис. 5.1
f (x,y,z)dxdydz f (ρsinθcos ,ρsinθsin ,ρcosθ)ρ2 sinθdρd dθ –
	T	T		тройной интеграл в сферических координатах.
				тройной интеграл в сферических координатах.

M(x,y,z)

M( , , )

	x ρsin θ cos ,		– связь декартовых координат
y			(x;y;z) со сферическими ко--
	y ρsin θ sin ,
		z ρ cos θ	ординатами (ρ; ;θ) (рис. 5.2).
x

Рис. 5.2
M γ(x,y,z)dxdydz – масса тела T с плотностью γ(x,y,z).
T

Статические моменты тела относительно плоскостей:

Mxy z γ(x,y,z)dxdydz – относительно координатной плоскости Oxy,

Myz

x γ(x,y,z)dxdydz – относительно координатной плоскости Oyz,

Mxz

y γ(x,y,z)dxdydz – относительно координатной плоскости Oxz.

Myz

, zc

Mxy

– координаты центра тяжести тела T .

В случае однородного тела (γ(x,y,z) – константа):

xdxdydz

ydxdydz

zdxdydz

, zc

dxdydz

Моменты инерции тела T :

Ixy z2

γ(x,y,z)dxdydz – относительно координатной плоскости Oxy,

Iyz x2

γ(x,y,z)dxdydz – относительно координатной плоскости Oyz,

Ixz y2

γ(x,y,z)dxdydz – относительно координатной плоскости Oxz,

Ixz (y2

z2) γ(x,y,z)dxdydz – относительно оси Ox,

Ix Ixy

Iy Ixy

Iyz (x2

z2) γ(x,y,z)dxdydz – относительно оси Oy,

Ixz

Iyz (x2

y2) γ(x,y,z)dxdydz – относительно оси Oz.

r2 γ(x,y,z)dxdydz – относительно некоторой оси l

(r – расстояние точки (x,y,z) тела до оси l),

IO (x2

y2 z2) γ(x,y,z)dxdydz – относительно начала координат.

5.4. Криволинейный и поверхностный интегралы

5.4.1. Криволинейный интеграл

Криволинейный интеграл по длине дуги (интеграл I рода)

f (x,y)ds f (x, (x)) 1 (x) 2dx –

AB a

криволинейный интеграл от функции z f (x,y) по длине дуги y (x).

f (x,y)ds f (x(t),y(t)) x (t) 2 y (t) 2dt –

AB		t1
		криволинейный интеграл от функции z f (x,y) по длине дуги,
		заданной параметрически	x x(t), y y(t).
L ds – длина (мера) дуги AB.
b	AB
b
		2	y (x).
	1 (x) dx – длина (мера) дуги		y (x).
a

Масса дуги с линейной плотностью γ(x,y)

(γ(x,y,z) – в случае пространственной кривой).

M γ ds.

Координаты центра тяжести дуги AB

xγds

yγds

zγds

, yc

, zc

γds

В случае однородной дуги (γ – константа):

xds

yds

zds

, yc

, zc

Криволинейный интеграл по координатам (интеграл II рода)

P(x,y)dx Q(x,y)dy

P(x, (x)) (x)Q(x, (x)) dx –

кривая AB задана уравнением y (x).

P(x,y)dx Q(x,y)dy P(x(t),y(t))x (t) Q(x(t),y(t)) y (t) dt –

AB	t1
	кривая AB задана параметрически x x(t), y y(t).

P(x,y,z)dx Q(x,y,z)dy R(x,y,z)dz

t2
		–
P(x(t),y(t),z(t))x (t) Q(x(t),y(t),z(t))y (t) R(x(t),y(t),z(t))z (t) dt
t1	x x(t), y y(t),z z(t).
пространственная кривая задана параметрически

Физический смысл криволинейного интеграла II рода:

P(x,y,z)dx Q(x,y,z)dy R(x,y,z)dz –

работа силы F P i Q j R k вдоль дуги AB.

При условии P Q криволинейный интеграл по любому замкнутому

y x

плоскому контуру C равен нулю: P(x,y)dx Q(x,y)dy 0.

(x1,y1)

В этом случае интеграл P(x,y)dx Q(x,y)dy не зависит от пути интег-

(x0 ,y0 )

рирования, подынтегральное выражение является полным дифференциалом некоторой функции U(x,y), т.е. P(x,y)dx Q(x,y)dy dU(x,y), где

x y x y

U(x,y) P(x,y0)dx Q(x,y)dy					или U(x,y) P(x,y)dx Q(x0,y)dy.
	x0	y0					x0	y0
	Формула Грина
				Q(x,y)		P(x,y)
	P(x,y)dx	Q(x,y)dy		Q(x,y)		P(x,y)	dxdy –
	P(x,y)dx	Q(x,y)dy					dxdy –
				x		y
C			D	x		y

область D ограничена контуром C.

Площадь области, ограниченной контуром C: S 1 xdy ydx.

Связь криволинейных интегралов I и II рода

На плоскости: P(x,y)dx Q(x,y)dy P(x,y)cosα Q(x,y)cosβ ds,

			L			L
где , – углы между касательной к плоской кривой L и осями координат.
Если параметрические уравнения кривой x x(t), y y(t), то
					y
cosα		x		, cosβ sinα	y			.
cosα				, cosβ sinα				.
		2	2		2		2
	x		y		x	y
В пространстве: P(x,y,z)dx Q(x,y,z)dy R(x,y,z)dz
			L	P(x,y)cosα Q(x,y)cosβ R(x,y)cosγ ds,
				P(x,y)cosα Q(x,y)cosβ R(x,y)cosγ ds,
				L
где , , – углы между касательной к пространственной кривой L и осями

координат.

Если параметрические уравнения кривой x x(t), y y(t),z z(t), то

cosα

,cosβ

, cosγ

5.4.2. Поверхностный интеграл

Поверхностный интеграл по площади поверхности (интеграл I рода)

F(x,y,z)dS F(x,y, f (x,y))		1 ( fx (x,y))2	( fy (x,y))2 dxdy –
S	D

поверхностный интеграл от функции F(x,y,z) по площади поверхности z f (x,y). Здесь D – проекция поверхности S на плоскость Oxy.

F(x,y,z)dS F(x(u,v),y(u,v),z(u,v)) EG M 2 dudv –

S D

поверхностный интеграл от функции F(x,y,z) по площади поверхности, заданной параметрически x x(u,v),y y(u,v),z z(u,v). Здесь D – область плоскости параметров u,v, функции

E (xu (u,v))2 (yu(u,v))2 (zu (u,v))2, G (xv(u,v))2 (yv(u,v))2 (zv(u,v))2,

M xu(u,v) xv (u,v) yu (u,v) yv(u,v) zu (u,v) zv (u,v).

S dS – площадь (мера) поверхности S .

M γ(x,y,z)dS – масса материальной поверхности S с поверхностной

плотностью γ(x,y,z).

Статические моменты поверхности S :

Mxy z γ(x,y,z)dS – относительно плоскости Oxy.

	S
M yz	x γ(x,y,z)dS – относительно плоскости Oyz.
	S
Mxz	y γ(x,y,z)dS – относительно плоскости Oxz.
	S
	Координаты центра тяжести поверхности S
xc	Myz	,	yc	M	xz	,	zc	Mxy	.
xc	M	,	yc			,	zc	M	.
	M			M				M

В случае однородной поверхности (γ(x,y,z) – константа):

	xdS				ydS		zdS
xc	S		,	yc	S	, zc	S	.
xc	dS		,	yc	dS	, zc	dS	.
	dS				dS		dS
	S				S		S
Моменты инерции поверхности S :
Ixy z2		γ(x,y,z)dS – относительно плоскости Oxy,
	S
Iyz x2		γ(x,y,z)dS – относительно плоскости Oyz,
	S

Ixz y2	γ(x,y,z)dS – относительно плоскости Oxz,
S
Ix (y2	z2 ) γ(x, y,z)dS	– относительно оси Ox,
S
Iy (x2	z2) γ(x,y,z)dS	– относительно оси Oy,
S
Iz (x2	y2) γ(x,y,z)dS	– относительно оси Oz,
S
Il r2 γ(x,y,z)dS– относительно некоторой оси l
S	(r – расстояние точки (x,y,z) поверхности до оси l),
	(r – расстояние точки (x,y,z) поверхности до оси l),
IO (x2	y2 z2) γ(x,y,z)dS – относительно начала координат.
S

Поверхностный интеграл по координатам (интеграл II рода)

F(x,y,z)dxdy F x,y, f (x,y) dxdy – поверхностный интеграл II рода

S D

от функции F(x,y,z), если поверхность S задана явным уравнением z f (x,y). Здесь D – проекция поверхности S на плоскость Oxy.

P(x,y,z)dydz Q(x,y,z)dxdz R(x,y,z)dxdy

(P(x,y,z) cosα Q(x,y,z) cosβ R(x,y,z) cosγ)dS –

выражение поверхностного интеграла II рода через интеграл I рода. Здесь cosα,cosβ,cosγ – направляющие косинусы нормали поверхности S .

Если поверхность задана неявным уравнением F(x,y,z) 0, то

cosα						Fx						,
cosα												,
			(Fx )2 (Fy )2 (Fz )2
cos						Fy							,
cos													,
					2			2		2
		(Fx )				(Fy )			(Fz )
cosγ						Fz					,

				2			2			2
				2			2			2
	(Fx )					(Fy )			(Fz )

знак выбирается в зависимости от стороны поверхности S .

Если поверхность задана параметрическими уравнениями

x x(u,v), y y(u,v), z z(u,v), то

cosα

, cosβ

, cosγ

A2 B2 C2

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.11.20232.11 Mб08984.pdf
#
25.11.20232.11 Mб08985.pdf
#
25.11.20232.11 Mб08986.pdf
#
25.11.20232.11 Mб08987.pdf
#
25.11.20232.12 Mб08988.pdf
#
25.11.20232.12 Mб08989.pdf
#
21.11.2023160.6 Кб0899.pdf
#
25.11.20232.12 Mб08990.pdf
#
25.11.20232.12 Mб08991.pdf
#
25.11.20232.12 Mб08992.pdf
#
25.11.20232.12 Mб08993.pdf