
8519
.pdf
(1,4) коэффициент затрат после сложения будет равен 3+1=4, поэтому, чтобы он стал равен нулю, четвертому столбцу надо придать потенциал, равный –4.
Действуя далее аналогично, последовательно получим: потенциал 1 для первой строки, –1 для третьего столбца, –3 для третьей строки и 0 для второго столбца.
Прибавляя полученные потенциалы к коэффициентам затрат (и по строкам, и
по столбцам), получаем следующую матрицу оценок:
|
6 |
5 |
6 |
4 |
|
|
0 |
1 |
0 |
0 |
|
|
. |
||||
|
4 |
0 |
0 |
0 |
|
|
0 |
0 |
1 |
4 |
|
|
|
Так как среди оценок клеток есть отрицательные, полученное распределе-
ние не является оптимальным. Выберем клетку (произвольно) с отрицательной оценкой, например, (4,4), и построим для нее означенный цикл пересчета. В
цикле, кроме выбранной клетки, должны, участвовать только заполненные клетки, в каждом столбце и в каждой строке цикла должно быть по две клетки.
Для клетки (4,4) цикл пересчета выглядит так:
|
(2,1) |
|
|
|
|
(2,4) |
|
|
|
|
|
|
|
4 |
+ |
|
|
8 |
– |
|
|
|
|||||
|
|
|
|
|
|
0 |
|
– |
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
(4,1) |
(4,4) |
|||
Найдем максимальное значение поставки, которое можно передвинуть по циклу как наименьшее значение поставки в «отрицательных» клетках. В нашем случае такая поставка равна 30. Заметим, что передвинув по циклу 30 единиц,
получим нулевые поставки сразу в двух клетках – (2,4) и (4,1). Если считать их обе пустыми, число базисных клеток уменьшится, чего допустить нельзя. По-
81
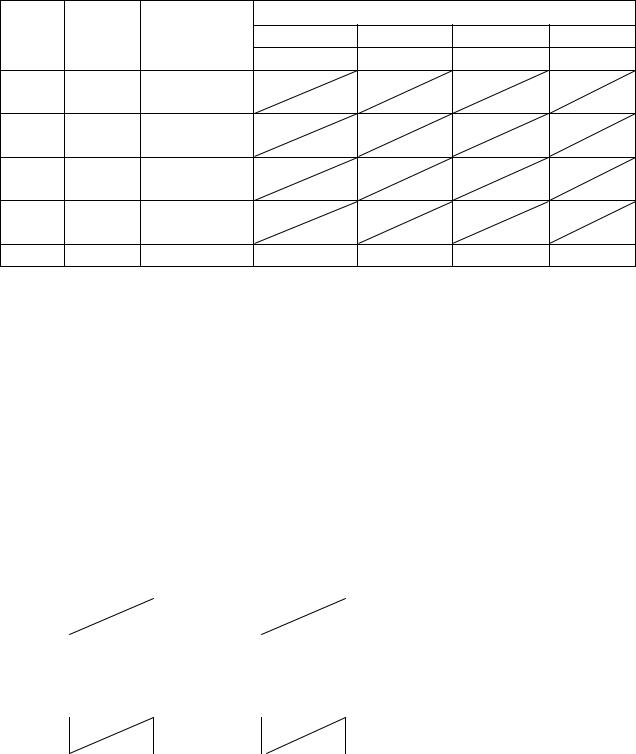
этому клетку (4,1) будем считать заполненной с поставкой, равной 0. Клетка |
|||||||
(2,4) становится пустой, в клетке (2,1) поставка 50. Получаем следующее ба- |
|||||||
зисное распределение. |
|
|
|
|
|
||
|
Постав |
Мощность |
|
Потребители и их спрос |
|
||
|
щики |
поставщи- |
1 |
|
2 |
3 |
4 |
|
|
ков |
50 |
|
50 |
40 |
60 |
-3 |
1 |
30 |
5 |
4 |
6 |
3 |
|
|
|
|
|
|
|
|
30 |
-4 |
2 |
70 |
4 |
5 |
5 |
8 |
|
|
|
|
50 |
|
|
20 |
|
-3 |
3 |
70 |
7 |
3 |
4 |
7 |
|
|
|
|
|
|
50 |
20 |
|
0 |
4 |
30 |
0 |
0 |
0 |
0 |
|
|
|
|
0 |
|
|
|
30 |
|
|
|
0 |
|
0 |
-1 |
0 |
|
Проверим полученное распределение поставок на оптимальность. |
|
|||||
|
Для этого составим матрицу оценок клеток при помощи потенциалов, как |
||||||
было описано ранее. |
|
|
|
|
|
||
|
|
2 |
1 |
2 |
0 |
|
|
|
|
|||
|
|
0 |
1 |
0 |
4 |
|
|
|
|
|||
|
|
. |
|
|
|
|||||||
|
|
4 |
0 |
0 |
4 |
|
|
|
|
|||
|
|
0 |
0 |
1 |
0 |
|
|
|
|
|||
|
|
|
|
|
|
|||||||
Опять есть отрицательная оценка – у клетки (4,3). Составим для нее озна- |
||||||||||||
ченный цикл пересчета. |
|
|
|
|
|
|
||||||
(2,1) |
|
|
|
|
|
(2,3) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
+ |
|
|
|
|
5 |
|
– |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
– |
|
|
0 |
+ |
|
|
|
|||||
|
|
|
|
|
|
|
|
(4,1) |
|
|
|
|
(4,3) |
|
|
|
|
|
|
82 |

Передаем по циклу 0 единиц. При этом количество поставок в клетках не |
||||||
изменится, но теперь заполненной (нулевой поставкой) считаем клетку (4,3), а |
||||||
клетку (4,1) – пустой. Получим следующее распределение поставок. |
|
|||||
|
Постав |
Мощность |
|
Потребители и их спрос |
|
|
|
щики |
поставщи- |
1 |
2 |
3 |
4 |
|
|
ков |
50 |
50 |
40 |
60 |
-2 |
1 |
30 |
5 |
4 |
6 |
3 |
|
|
|
|
|
|
30 |
-4 |
2 |
70 |
4 |
5 |
5 |
8 |
|
|
|
50 |
|
20 |
|
-3 |
3 |
70 |
7 |
3 |
4 |
7 |
|
|
|
|
50 |
20 |
|
1 |
4 |
30 |
0 |
0 |
0 |
0 |
|
|
|
|
|
0 |
30 |
|
|
|
0 |
0 |
-1 |
-1 |
|
Опять составляем матрицу оценок (значение потенциалов по сравнению с |
|||||
предыдущей таблицей изменилось). |
|
|
|
|||
|
3 |
2 |
3 |
0 |
|
|
0 |
1 |
0 |
3 |
|
|
|
||||
|
4 |
0 |
0 |
3 |
|
|
1 |
1 |
0 |
0 |
|
|
|
В матрице нет отрицательных оценок, следовательно, полученное распре-
деление оптимально. Посчитаем суммарные затраты на перевозку этого рас-
пределения поставок.
Fmin 4 50 3 50 5 20 4 20 3 30 620 .
|
0 |
0 |
0 |
30 |
|
|
50 |
0 |
20 |
0 |
|
Ответ: F=620, оптимальное распределение |
. |
||||
|
0 |
50 |
20 |
0 |
|
|
|
83
4.2. Элементы теории матричных игр
Задача 1. Определить нижнюю и верхнюю цену игры, заданной платежной
|
|
3 |
2 |
1 |
|
|
|
|
|
|
|
матрицей |
P |
1 |
1 |
1 |
. Имеет ли игра седловую точку? |
|
|
2 |
0 |
4 |
|
|
|
|
Решение. Найдем по каждой строчке платежной матрицы минимальное число αi min(ai1,ai2 ,ai3 ) – это гарантированный выигрыш игрока А при выбо-
ре им соответствующей стратегии. Чтобы получить максимально возможный гарантированный выигрыш, игрок А должен выбрать ту стратегию, для которой
αij |
имеет максимальное значение – α min(a1,a2 ,a3) – это нижняя цена игры. |
|
|
Для игрока В |
выберем по каждому столбцу максимальное число |
β j |
min(a1 j ,a2 j ,a3 j ) |
– это гарантированный проигрыш игрока В при выборе |
им стратегии B j . Найдем минимальное из этих чисел β min(β1,β2 ,β3 ) – это верхняя цена игры. Занесем полученные данные в таблицу.
|
|
|
B1 |
|
B2 |
B3 |
|
|
|
|
A |
|
3 |
|
-2 |
1 |
1 |
min 3, 2,1 2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
A |
|
1 |
|
-1 |
1 |
2 |
min 1, 1,1 1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
A |
|
2 |
|
0 |
4 |
3 |
min 2,0, 4 0 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
β1 max(3,1, 2) 3 |
|
β2 max( 2, 1,0) 0 |
β3 max(1,1, 4) 4 |
max 2, 1, 0 0 |
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
β max(3, 0, 4) 0 |
|
|
Нижняя цена игры |
α 0 |
равна верхней цене игры β 0 . |
Значит, игра имеет |
||||||
седловую точку. Для игрока А оптимальная стратегия – A3 , для игрока В опти-
мальная стратегия – B2 .
Ответ: α β 0 , игра имеет седловую точку, оптимальные стратегии ( A3 , B2 ) .
Задача 2. (Сведение матричной игры |
к |
задаче линейного |
|||
|
2 |
- 3 |
4 |
|
|
|
|
|
|
|
|
программирования). Дана платежная матрица Р |
- 3 |
4 5 |
, α 3 4 |
β . |
|
|
4 |
5 |
6 |
|
|
|
|
|
|||
84 |
|
|
|
|
|
Прибавляя ко всем элементам матрицы (Pij ) число k= 5, приходим к мат-
|
|
|
|
|
|
|
|
|
7 |
2 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рице модифицированной игры |
Р |
2 |
9 |
0 |
|
, которой соответствует задача |
|||||||
|
|
|
|
|
|
|
|
|
9 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|||
линейного программирования. |
|
|
|
|
|
|
|||||||
х1 х2 |
х3 min |
|
|
|
|
|
|
||||||
7х 2х |
2 |
9х 1 |
|
|
|
|
|
|
|||||
|
|
1 |
|
3 |
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
||
2х1 9х2 |
|
|
|
|
|
|
|||||||
9х 11х |
1 |
|
|
|
|
|
|
||||||
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
х |
i |
1, |
i 1,3. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Воспользовавшись симплекс-методом, находим решение:
х* |
1 |
, х* |
1 |
|
, х* |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
20 |
2 |
10 |
|
3 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, |
цена модифицированной игры |
|
( )* |
|
1 |
|
|
5 |
, а |
||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
х* х* х* |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
||
цена исходной игры * ( )* 5 0 . При этом |
р* ( )* x |
|
|
|
|||||||||||||||||||
, i 1,3, т. е. опти- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
i |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
||
мальная смешанная стратегия первого игрока SA |
|
|
, |
|
, |
|
. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
|
4 |
|
|
|
|
|
|
|
|
В рассматриваемой игре Pij Т Pij и S*A S*В . Нетрудно найти оптималь-
ную смешанную стратегию второго игрока, решив соответствующую задачу линейного программирования, и убедиться в том, что она совпадает с опти-
мальной смешанной стратегией первого игрока.
Завершая рассмотрение игр двух участников с нулевой суммой без седло-
вых точек, заметим, что при использовании смешанных стратегий перед каж-
дой партией игры каждым игроком запускается некий механизм (бросание мо-
неты, игральной кости или использование датчика случайных чисел), обеспечи-
вающий выбор каждой чистой стратегии с заданной вероятностью. Как мы уже
отмечали, смешанные стратегии представляют собой математическую модель
85

гибкой тактики, при использовании которой противник не знает заранее, с ка-
кой обстановкой ему придется столкнуться в каждой следующей партии игры.
При этом ожидаемые теоретические результаты игры, при неограниченном воз-
растании числа разыгрываемых партий, стремятся к их истинным значениям.
Задача 3. Теории игр (аналитическое решение и имитационная мо-
дель)
Игра задана платежной матрицей |
10 |
7 |
|
A |
|
. |
|
|
|
8 |
|
|
|
11 |
|
1)Решить игру аналитически.
2)Провести моделирование результатов игры с помощью таблицы рав-
номерно распределенных случайных чисел, разыграв 30 партий; определить от-
носительные частоты использования чистых стратегий каждым игроком и средний выигрыш, сравнив результаты с полученными теоретически в п.1.
Решение: |
|
|
|
|
|
1. Найдем нижнюю и верхнюю цену игры. |
|
||||
|
|
|
|
|
|
B |
B1 |
B2 |
min в строке |
|
|
A |
|
|
|||
|
|
|
|
|
|
A1 |
10 |
7 |
7 |
|
|
A2 |
8 |
11 |
8 |
|
|
max в столбце |
10 |
11 |
= 8 |
|
|
= 10 |
|
|
|||
|
|
|
|
|
|
, следовательно, игра не имеет седловой точки, решение будет в сме- |
|||||
шанных стратегиях. |
|
|
|
|
|
Найдем аналитически оптимальную стратегию игрока А |
и |
||||
соответствующую цену игры . |
|
||||
Так как |
– оптимальная, то она должна гарантировать средний выиг- |
||||
рыш игроку А, равный цене игры, при любом поведении игрока В:
для стратегии В1: 10 p1 8 p2 ;
для стратегии В2: 7 p1 11p2 .
86

С учетом того, что сумма вероятностей смешанной стратегии равна 1, по-
лучаем систему уравнений:
10 p |
|
8 p |
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
11p2 |
, |
|
|
|
|
|
|
|
|
|
|
|
||||||
7 p1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
p |
p |
2 |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычтем из первого уравнения второе: 3 p1 3 p2 0 |
или p1 p2 . Значит: |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
p |
|
1 |
, |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p |
p |
|
, |
|
|
|
p2 |
|
|
|
|
, |
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
||||||||||||
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
p1 |
p2 1, |
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|||||||
7 p |
11p |
|
, |
7 |
|
|
11 |
|
9. |
|
||||||||||
|
|
|
|
|
||||||||||||||||
2 |
|
|
|
|
|
|
2 |
|
2 |
|
|
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Итак: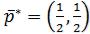 , = 9.
, = 9.
Аналогично получаем систему для нахождения смешанной стратегии игрока В.
10q1 7q2 ,8q1 11q2 ,
q1 q2 1.
Вычтем из первого уравнения второе: 2q 4q |
2 |
0 Откуда, |
q 2q |
2 |
подставим |
1 |
|
1 |
|
впервое уравнение (Вместо подставим найденное значение для игрока А
= 9):
Итак: .
.
Ответ: 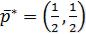 ,
, 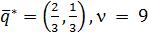 .
.
87
Проведем моделирование результатов решения с помощью таблицы рав-
номерно распределенных случайных чисел. Для 30 партий хватит 60 чисел, на основе которых будут выбираться стратегии игроками. Используемые случай-
ные числа сгенерированы в MS Excel функцией =СЛЧИС(). В приложении дос-
таточно много чисел, но использовать для моделирования можно любые 60,
выбранные произвольно с любого места таблицы. Выберем 60 чисел:
0,02988 |
0,12558 |
0,25974 |
0,17641 |
0,00937 |
0,52264 |
0,08086 |
0,84858 |
0,99427 |
0,49452 |
0,61109 |
0,49042 |
0,61076 |
0,65834 |
0,25579 |
0,80641 |
0,07675 |
0,84419 |
0,18268 |
0,29702 |
0,76606 |
0,95854 |
0,20704 |
0,45154 |
0,27367 |
0,56261 |
0,30037 |
0,96485 |
0,47252 |
0,55084 |
0,73868 |
0,56421 |
0,07183 |
0,99420 |
0,11184 |
0,80524 |
0,42897 |
0,45031 |
0,05350 |
0,67078 |
0,94483 |
0,25710 |
0,39190 |
0,72491 |
0,88888 |
0,03791 |
0,50773 |
0,63034 |
0,94091 |
0,80165 |
0,41647 |
0,88664 |
0,83519 |
0,46930 |
0,39285 |
0,34159 |
0,77252 |
0,65987 |
0,48750 |
0,79735 |
0,51314 |
0,22625 |
0,06211 |
0,39299 |
0,84336 |
0,80859 |
0,52694 |
0,73306 |
0,36874 |
0,93390 |
0,71749 |
0,46727 |
0,18182 |
0,45791 |
0,08667 |
0,58570 |
0,75495 |
0,68645 |
0,90270 |
0,87484 |
0,99401 |
0,82235 |
0,89122 |
0,33631 |
0,42694 |
0,37053 |
0,70413 |
0,59805 |
0,40425 |
0,96181 |
0,41244 |
0,24426 |
0,37553 |
0,09464 |
0,56208 |
0,68889 |
0,59503 |
0,92378 |
0,03108 |
0,33182 |
Будем выбирать стратегии игроков, используя геометрическое определе-
ние вероятности. Так как все случайные числа из отрезка [0; 1], то чтобы стра-
тегия А1 появлялась примерно в половине случаев, будем ее выбирать если случайное число меньше 0,5; в остальных случаях выбирается стратегия А2.
Аналогично для игрока В. Стратегию В1 будем выбирать, если соответствую-
щее случайное число меньше 2/3 0,67, в противном случае выбираем стратегию В2.
Заполним расчетную таблицу (Средний выигрыш игрока А считаем, как отношение накопленного выигрыша к количеству сыгранных партий):
|
Случайное |
Стратегия |
Случайное |
Стратегия |
|
Накоплен- |
Средний |
|
Номер |
Выигрыш |
выигрыш |
||||||
число иг- |
игрока А |
число иг- |
игрока В |
ный выиг- |
||||
партии |
А |
А (цена |
||||||
рока А |
А1: < 0,5 |
рока В |
В1: < 0,667 |
рыш А |
||||
|
|
игры) |
||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1. |
0,029 |
А1 |
0,125 |
В1 |
10 |
10 |
10,000 |
|
2. |
0,611 |
А2 |
0,490 |
В1 |
8 |
18 |
9,000 |
|
3. |
0,766 |
А2 |
0,958 |
В2 |
11 |
29 |
9,667 |
|
4. |
0,738 |
А2 |
0,564 |
В1 |
8 |
37 |
9,250 |
|
5. |
0,944 |
А2 |
0,257 |
В1 |
8 |
45 |
9,000 |
|
6. |
0,416 |
А1 |
0,886 |
В2 |
7 |
52 |
8,667 |
88
7. |
0,513 |
А1 |
0,226 |
В1 |
10 |
62 |
8,857 |
8. |
0,717 |
А2 |
0,467 |
В1 |
8 |
70 |
8,750 |
9. |
0,994 |
А2 |
0,822 |
В2 |
11 |
81 |
9,000 |
10. |
0,412 |
А1 |
0,244 |
В1 |
10 |
91 |
9,100 |
11. |
0,259 |
А1 |
0,176 |
В1 |
10 |
101 |
9,182 |
12. |
0,610 |
А2 |
0,658 |
В1 |
8 |
109 |
9,083 |
13. |
0,207 |
А1 |
0,451 |
В1 |
10 |
119 |
9,154 |
14. |
0,071 |
А1 |
0,994 |
В2 |
7 |
126 |
9,000 |
15. |
0,391 |
А1 |
0,724 |
В2 |
7 |
133 |
8,867 |
16. |
0,835 |
А2 |
0,469 |
В1 |
11 |
144 |
9,000 |
17. |
0,062 |
А1 |
0,392 |
В1 |
10 |
154 |
9,059 |
18. |
0,181 |
А1 |
0,457 |
В1 |
10 |
164 |
9,111 |
19. |
0,891 |
А2 |
0,336 |
В1 |
8 |
172 |
9,053 |
20. |
0,375 |
А1 |
0,094 |
В1 |
10 |
182 |
9,100 |
21. |
0,009 |
А1 |
0,522 |
В1 |
10 |
192 |
9,143 |
22. |
0,255 |
А1 |
0,806 |
В2 |
7 |
199 |
9,045 |
23. |
0,273 |
А1 |
0,562 |
В1 |
10 |
209 |
9,087 |
24. |
0,111 |
А1 |
0,805 |
В2 |
7 |
216 |
9,000 |
25. |
0,888 |
А2 |
0,037 |
В1 |
8 |
224 |
8,960 |
26. |
0,392 |
А1 |
0,341 |
В1 |
10 |
234 |
9,000 |
27. |
0,843 |
А2 |
0,808 |
В2 |
11 |
245 |
9,074 |
28. |
0,086 |
А1 |
0,585 |
В1 |
10 |
255 |
9,107 |
29. |
0,426 |
А1 |
0,370 |
В1 |
10 |
265 |
9,138 |
30. |
0,562 |
А2 |
0,688 |
В2 |
11 |
276 |
9,200 |
Таким образом, в результате моделирования в 30 партиях цена игры (средний выигрыш) равен 9,2. Этот результат согласуется с теоретической ценой игры 9.
Из 30 партий игрок А 18 раз применял стратегию А1, 12 раз – стратегию А2. Игрок В 21 раз применял стратегию В1, 9 раз – стратегию В2. Частоты ис-
пользования игроками своих чистых стратегий соответственно равны:
p=(18/30;12/30)=(0,6;0,4), q=(21/30;9/30)=(0,7;0,3). Сравнивая с теоретически-
ми оптимальными стратегиями 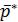 =(0,5; 0,5) и
=(0,5; 0,5) и 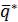 =(0,67; 0,33) можно сделать вывод, что результаты моделирования достаточно близко соответствуют теоре-
=(0,67; 0,33) можно сделать вывод, что результаты моделирования достаточно близко соответствуют теоре-
тическим вероятностям даже для небольшого количества партий.
89

4.3. Системы массового обслуживания
Задача 1.
Пункт по ремонту радиотехники работает в режиме отказа с одним мастером. Интенсивность потока заявок 1, производительность мастера 1.3.
Определить предельные значения относительной пропускной способности Q,
абсолютной пропускной способности А и вероятность отказа Ротк телефонной линии. Определить также среднее время обслуживания одного вызова, среднее время простоя канала и вероятность того, что канал свободен или занят.
Исчисляем показатели обслуживания для одноканальной СМО
1. Интенсивность нагрузки.
Интенсивность нагрузки ρ=0.769 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.
2.Время обслуживания.
3.Вероятность, что канал свободен (доля времени простоя канала).
Следовательно, 57% в течение часа канал будет не занят, время простоя
равно tпр = 33.9 мин.
4.Доля заявок, получивших отказ (вероятность отказа). pотк = 1 - p0 = 1 - 0.565 = 0.43
Значит, 43% из числа поступивших заявок не принимаются к обслуживанию.
5.Относительная пропускная способность.
Доля обслуживаемых заявок, поступающих в единицу времени:
90
