
8510
.pdf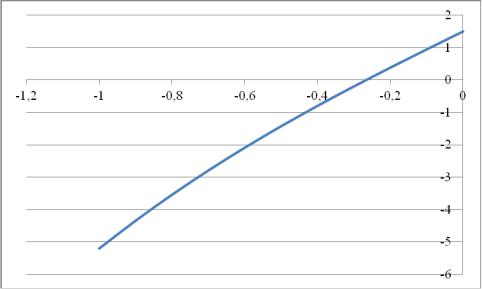
30
y x3 0,2x2 5,5x 1,5
Рис. 8. Графическое отделение корня для уравнения x3 0,2x2 5,5x 1,5 0 .
Результаты проведенных вычислений удобно представлять в виде
таблицы (табл. 3). Очевидно, что процесс уточнения корня достаточно бы-
стро сходится, |
а t 0,26645 |
или с |
заданной степенью точности |
|||||||
t 0,266. |
|
|
|
|
|
|
|
|
|
|
|
|
Уточнение корня уравнения методом хорд |
|
Таблица 3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Номер |
xn 1 |
|
f xn 1 |
|
xn |
|
xn xn 1 |
|
|
|
|
|
|
|
||||||
|
итерации |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
1,5 |
|
-0,22388 |
0,2238806 |
|
||
|
2 |
-0,22388 |
|
0,247411 |
|
-0,25913 |
0,03524983 |
|
||
|
3 |
-0,25913 |
|
0,043953 |
|
-0,26534 |
0,00620967 |
|
||
|
4 |
-0,26534 |
|
0,007867 |
|
-0,26645 |
0,00110978 |
|
||
3.5. Метод касательных (метод Ньютона)
Будем строить касательную к кривой y f (x) . Каждое приближе-
ние к точному решению будет абсциссой точки пересечения соответст-
вующей касательной и оси OX . Важным является вопрос о выборе на-
чального приближения x0 a; b . Начальное приближение удовлетворяет неравенству f (x0 ) f (x0 ) 0 . Принято следующее правило: если f (x) и

31
f (x) одного знака на отрезке a; b , то следует брать x0 b (рис. 9), а ес-
ли разных знаков, то x0 a .
После того как начальное приближение выбрано, строят касатель-
ную к кривой y f (x) в точке B0 x0 ; f (x0 ) , уравнение которой имеет вид:
y f (x0 ) f (x0 ) x x0 .
Следующее приближение корня x1 найдем, исходя из того, что это
абсцисса точки пересечения касательной и оси абсцисс, а значит |
y 0 , |
||||||
следовательно: |
|
|
|
|
|
||
|
x1 x0 |
|
f (x0 ) |
. |
|
||
|
|
|
|
||||
|
|
|
|
f (x0 ) |
|
|
|
|
Для n го приближения будем иметь рекуррентную формулу: |
|
|||||
|
xn xn 1 |
|
f (xn 1 ) |
, |
|
(3.17) |
|
|
|
|
|
|
|||
|
|
|
f (xn 1 ) |
|
|
|
|
где |
|
|
|
|
|
|
|
f (xn 1 ) 0 . |
|
|
|
|
|
||
y |
B0 |
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
a |
|
t |
|
x0 |
|
|
|
|
|
|
O |
x2 x1 b |
x |
|||
A
Рис. 9. Метод Ньютона (касательных)

32
Теорема 5 (достаточное условие сходимости метода Ньютона).
Пусть f x определена и дважды дифференцируема на отрезке a; b , при-
чем f (a) f (b) 0 , производные f (x) и f (x) сохраняют знак на отрезке
a; b изоляции корня t , а |
|
|
|
|
|
|
|
|
|
|
|
|
f x 0 . Пусть также существуют положитель- |
||||||||||||
ные числа m и M такие, что |
|
|
|
m1 |
, |
|
|
|
M 2 |
, |
x a; b . Тогда, ис- |
|
|
|
|
|
|||||||||
|
f (x) |
|
|
f (x) |
|
|||||||
ходя из начального приближения x0 a; b , удовлетворяющего неравенст-
ву f x0 f x0 0 , можно построить последовательность, определяемую рекуррентной формулой и сходящуюся к единственному корню t на от-
резке a; b . Тогда погрешность приближений к t , найденных методом ка-
сательных, оценивается формулой
t x |
n |
|
|
M 2 |
|
|
t x |
n 1 |
|
2 |
, |
|
|
|
|||||||||
|
2m1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Обычно берут M 2 |
max |
|
f |
|
|
, m1 |
|
|
|
||||||
|
(x) |
|
|||||
|
a;b |
|
|
|
|
|
|
|
|
|
|
|
|
На практике итерационный процесс нии условия
xn t xn xn 1
где – заданная точность.
n 1,2,... (3.18)
min |
|
|
|
. |
|
|
|||
|
f x |
|
||
a;b |
|
|
|
|
|
|
|
|
останавливают при выполне-
, |
(3.19) |
Пример. Методом Ньютона с точностью 10 2 уточнить корень
уравнения f x 0 , где |
f x x 2 |
e x , |
x 0,5;1,0 . |
Решение. |
|
|
|
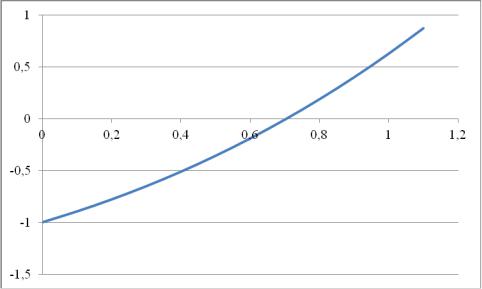
Врезультате графического отделения корня (рис. 10), делаем вывод
осуществовании и единственности корня на заданном отрезке. Начальное
приближение x0 1 (правый конец отрезка), так как |
f 1 0 , |
|
||||||||||
f 1 0 . |
||||||||||||
Продолжим |
вычисления |
по |
рекуррентной |
формуле |
(3.17): |
|||||||
x |
1 |
f 1 |
|
0,733 , x |
|
0,733 |
|
f 0,733 |
0,7038 , проверим условие ос- |
|||
1 |
|
|
|
2 |
|
|
|
|
|
|
||
|
|
f 1 |
|
|
|
|
|
f 0,733 |
|
|
||
33
тановки процесса вычислений (3.19) |
|
x2 x1 |
|
|
0,092 . Значит процесс |
||||||
|
|
||||||||||
необходимо продолжить. На следующем |
шаге получим x3 0,7034, |
||||||||||
|
x |
3 |
x |
2 |
|
0,3414 10 3 . Процесс нужно остановить и взять t 0,70 . |
|||||
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
y x2 e x
Рис. 10. Отделение корня для уравнения x2 e x 0
4. Решение систем линейных алгебраических уравнений
Системы линейных алгебраических уравнений (СЛАУ) можно ре-
шать как с помощью прямых, так и итерационных методов. Для систем уравнений средней размерности чаще используют прямые методы.
Итерационные методы применяют главным образом для решения задач большой размерности, когда использование прямых методов невоз-
можно из-за ограничений в доступной оперативной памяти ЭВМ или из-за необходимости выполнения чрезмерно большого числа арифметических операций.
4.1.Прямые методы решения систем линейных алгебраических уравнений
Система линейных алгебраических уравнений с вещественными ко-
эффициентами имеет вид:
34
a11x1 a12 x2 a13 x3 ... |
a1m xm b1 |
|
a21x1 a22 x2 a23 x3 ... |
a2m xm b2 |
|
a31x1 a32 x2 a33 x3 ... |
a3m xm b3 |
(4.1) |
.....................................................
am1 x1 am2 x2 am3 x3 ... am mxm bm .
Вматричной форме записи эта система принимает вид:
|
|
Ax b , |
|
|
|
|
|
|
|
(4.2) |
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
a11 |
a12 a13 ... a1m |
|
|
x1 |
|
|
b1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
a21 |
a22 a23 ... a2m |
|
|
x2 |
|
|
b2 |
|
||
A |
|
a32 a33 ... a3m |
|
x |
|
|
|
b |
|
|
|
a31 |
, |
x3 |
, |
b3 |
. |
||||||
|
........................ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
am1 |
am2 am3 ... amm |
|
xm |
|
bm |
|||||
Необходимо вычислить вектор x , являющийся решением системы
(4.2), по входному данному – вектору b . Будем предполагать, что матрица
A задана и является невырожденной. Известно, что в этом случае решение системы существует, единственно и устойчиво по входным данным. Это
означает, что рассматриваемая задача корректна.
Пусть x* (x1*, x2*, ...,xm* )T – приближенное решение системы (4.1).
Будем стремиться к получению решения, для которого погрешность
e x x* мала. Тем не менее, заметим, что качество полученного решения далеко не всегда характеризуется тем, насколько мала погрешность x x* .
Иногда вполне удовлетворительным является критерий малости невязки r b Ax* . Вектор r показывает, насколько отличается правая часть сис-
темы от левой, если подставить в нее приближенное решение. Заметим,
что r Ax Ax* A(x x*) , и поэтому погрешность и невязка связаны ра-
венством:
e x x* A 1r .
35
4.1.1. Метод Гаусса
Рассмотрим один из самых распространенных методов решения систем линейных алгебраических уравнений – метод Гаусса. Этот метод также называют методом последовательного исключения неизвестных.
Вычисления с помощью метода Гаусса состоят из двух основных этапов, называемых прямым ходом и обратным ходом (обратной подста-
новкой). Прямой ход метода Гаусса заключается в последовательном ис-
ключении неизвестных из системы (4.1) для преобразования ее к эквива-
лентной системе с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода.
1. Схема единственного деления. Рассмотрим простейший вариант метода Гаусса, называемой схемой единственного деления.
Прямой ход состоит из m-1 шагов исключения.
1–й шаг. Целью этого шага является исключение неизвестного x1
из уравнений с номерами i 2,3,...,m . Предположим, что коэффициент a11 0 . Будем называть его главным (или ведущим) элементом 1-го шага.
Найдем величины:
i1 ai1 / a11 (i 2, 3,...,m) , |
(4.3) |
называемые множителями 1–го шага. Вычтем последовательно из второго,
третьего,…, m –го уравнений системы (4.1) первое уравнение, умноженное соответственно на 21, 31,..., m1 x1 . Это позволит обратить в нуль коэф-
фициенты при x1 во всех уравнениях, кроме первого. В результате полу-
чим эквивалентную систему:
a11x1 a12 x2 |
|
a13x3 |
... a1m xm b1, |
|
|
||||||||
a(1) x |
2 |
a(1) x |
3 |
... a(1) |
x |
m |
b(1) |
, |
|||||
22 |
|
23 |
2m |
|
|
2 |
|
|
|||||
a(1) x |
2 |
a(1) x |
3 |
... a(1) x |
m |
b(1) |
, |
(4.4) |
|||||
32 |
|
33 |
3m |
|
|
3 |
|
|
|||||
............................................. |
|
|
|||||||||||
a(1) |
x |
2 |
a(1) x |
... a(1) |
|
x |
m |
b(1) |
, |
||||
m2 |
|
|
m3 |
3 |
mm |
|
|
m |
|
|
|||
36
в которой a(1) и b(1) (i, j 2,3,...,m) вычисляются по формулам: |
|
||||||||||||
ij |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
a(1) a |
ij |
|
a |
, |
b(1) |
b |
|
b . |
(4.5) |
|||
|
ij |
|
|
|
i1 1 j |
|
i |
i |
|
i1 1 |
|
|
|
2–й шаг. Целью этого шага является исключение неизвестного |
x2 |
||||||||||||
из уравнений с номерами i 3,4,...,m |
. Пусть a |
(1) 0 , где |
a(1) – коэффици- |
||||||||||
|
|
|
|
|
|
|
|
|
22 |
|
22 |
|
|
ент, называемый главным (или ведущим) элементом 2-го шага: |
|
||||||||||||
|
|
|
|
a(1) |
/ a(1) (i 3, 4,...,m) |
|
|
||||||
|
|
|
|
i2 |
|
i2 |
|
22 |
|
|
|
|
|
и вычтем последовательно из третьего, четвертого, … |
m го уравнений |
||||||||||||
системы (4.4) |
второе |
уравнение, |
умноженное соответственно |
на |
|||||||||
32 , 42 ,..., m2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
В результате получим систему:
|
a11x1 a12 x2 a13x3 |
... a1m xm |
b1, |
|
|
|
|||||||
|
|
a(1) x |
a(1) x |
... a(1) x |
b(1) , |
|
|
|
|||||
|
|
22 2 |
|
|
23 3 |
|
|
2m m |
|
2 |
|
|
|
|
|
|
|
|
a(2) x |
|
... a(2) x |
|
b(2) , |
|
|
(4.6) |
|
|
|
|
|
|
33 3 |
|
3m m |
3 |
|
|
|
||
|
|
............................................. |
|
|
|
||||||||
|
|
|
|
|
a(2) x |
|
... a(2) x |
|
b(2). |
|
|
|
|
|
|
|
|
|
m3 3 |
|
mm m |
m |
|
|
|
||
Здесь коэффициенты |
a (2) и |
b(2) (i, j 3, 4,...,m) |
вычисляются по |
||||||||||
|
|
|
|
ij |
|
|
i |
|
|
|
|
|
|
формулам: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a(2) |
a(1) |
i2 |
a(1) , |
|
b(2) |
b(2) |
b(1) |
i2 |
b(1) . |
|||
|
ij |
ij |
|
2 j |
|
i |
i |
|
i |
|
2 |
||
Аналогично проводятся остальные шаги. |
Опишем очередной k й |
||||||||||||
шаг. |
|
|
|
|
|
|
|
|
|
|
|
|
|
k й шаг. В предположении, |
что главный (ведущий) элемент k-го |
||||||||||||
шага a (k 1) |
отличен от нуля, вычислим множители k го шага: |
||||||||||||
kk |
|
|
|
|
|
|
|
|
|
|
|
|
|
ik aik(k 1) / akk(k 1)
(i k 1,...,m)
37
и вычтем последовательно из k 1 го, …, m го уравнений полученной на предыдущем шаге системы k е уравнение, умноженное соответствен-
но на k 1,k , k 2,k ,..., mk .
После m 1 го шага исключения получим систему уравнений
a11x1 a12 x2 |
a13x3 |
... a1m xm |
|
b1, |
|
|
||||
a(1) x |
2 |
a(1) x |
3 |
... a(1) |
x |
m |
b(1) |
, |
|
|
22 |
23 |
2m |
|
2 |
|
|
||||
|
|
a(2) x |
... a(2) x |
m |
b(2) |
, |
(4.7) |
|||
|
|
33 |
3 |
3m |
|
|
3 |
|
|
|
............................................. |
|
|
||||||||
|
|
|
|
a(m 1) x |
|
|
b(m 1) |
, |
||
|
|
|
|
mm |
|
m |
m |
|
|
|
матрица A(m 1) которой является верхней треугольной. На этом вычисле-
ния прямого хода заканчиваются.
Обратный ход. Из последнего уравнения системы (4.7) находим xm .
Подставляя найденное значение xm в предпоследнее уравнение, получим xm 1 . Осуществляя обратную подстановку, далее последовательно находим xm 2 , xm 3,...,x1. Вычисления неизвестных здесь проводятся по формулам:
x |
|
b(m 1) |
/ a (m 1) , |
|
|
|
|
|
|
|
m |
m |
mm |
|
|
|
|
|
(4.8) |
|
|
(b(k 1) |
a (k 1) x |
|
... a (k 1) x |
|
) / a (k 1) |
|
|
x |
k |
k 1 |
m |
, |
(k m 1,...,1). |
||||
|
k |
k ,k 1 |
km |
kk |
|
|
2. Метод Гаусса с выбором главного элемента по столбцу (схема частичного выбора). Описание метода. На k м шаге прямого хода коэф-
фициенты уравнений системы с номерами i k 1,...,m преобразуются по формулам:
a(k ) a(k 1) |
|
a(k 1) |
, |
b(k ) b(k 1) |
|
b(k 1) |
, |
i k 1,...,m . (4.9) |
||
ij |
ij |
ik |
kj |
|
i |
i |
ik |
k |
|
|
Во избежание сильного роста коэффициентов системы и связанных
сэтим ошибок нельзя допускать появления больших множителей ik .
Вметоде Гаусса с выбором главного элемента по столбцу гаранти-
руется, что |
|
ik |
|
1 для всех k 1, 2,...,m 1 и i k 1,...,m. Отличие этого |
|
|
варианта метода Гаусса от схемы единственного деления заключается в
38
том, что на k м шаге исключения в качестве главного элемента выбирают
максимальный по модулю коэффициент aik k при неизвестной xk в уравне-
ниях с номерами i k, k 1,...,m . Затем соответствующее выбранному ко-
эффициенту уравнение с номером ik меняют местами с k м уравнением
системы для того, чтобы главный элемент занял место коэффициента akk(k 1) . После этой перестановки исключение неизвестного xk производят,
как в схеме единственного деления.
3. Метод Гаусса с выбором главного элемента по всей матрице
(схема полного выбора).
В этой схеме допускается нарушение естественного порядка ис-
ключения неизвестных.
На 1–м шаге метода среди элементов aij определяют максимальный
по модулю элемент ai1 j1 . Первое уравнение системы и уравнение с номе-
ром i1 меняют местами. Далее стандартным образом производят исключе-
ние неизвестного x j1 из всех уравнений, кроме первого.
На k м шаге метода среди коэффициентов aij(k 1) при неизвестных в уравнениях системы с номерами i k,...,m выбирают максимальный по
модулю коэффициент ai(kj 1) . Затем k е уравнение и уравнение, содержа-
k k
щее найденный коэффициент, меняют местами и исключают неизвестное x jk из уравнений с номерами i k 1,...,m .
На этапе обратного хода неизвестные вычисляют в следующем по-
рядке: x jm , x jm 1 ,...,x j1 .
Пример. Методом Гаусса решить систему:
|
|
|
39 |
|
|
|
10x1 |
6x 2 2x3 |
|
25, |
|
||
|
5x1 |
x2 |
2x3 |
4x4 |
14, |
|
|
(4.10) |
|||||
|
3x1 |
5x2 |
x3 |
x4 |
10, |
|
|
|
|||||
|
|
6x 2 2x3 2x4 |
8. |
|
||
|
|
|
||||
Прямой ход. 1-й шаг. Вычислим множители:
21 a21 /a11 5/10 0,5; 31 a31 / a113/10 0,3; 41 a41 / a11 0 /10 0.
Вычитая из второго, третьего и четвертого уравнений системы (4.10) пер-
вое уравнение, умноженное на 21, |
31 и |
41 соответственно получим: |
||||
10x1 |
6x2 |
|
2x3 |
|
25, |
|
|
2x2 |
3x3 4x4 |
1,5, |
|
||
|
(4.11) |
|||||
|
3,2x2 0,4x3 |
x4 |
2,5, |
|||
|
|
|||||
|
6x2 2x3 |
2x4 8. |
|
|||
|
|
|||||
2-й шаг. Вычислим множители:
32 a32(1) / a22(1) 3,2 /( 2) 1,6; 42 6 /( 2) 3.
Вычитая из третьего и четвертого уравнений системы (4.11) второе урав-
нение, умноженное на 32 |
и 42 соответственно, приходим к системе: |
||||
10x1 6x2 |
2x3 |
25, |
|
||
|
2x2 |
3x3 4x4 |
1,5, |
|
|
|
(4.12) |
||||
|
4,4x3 |
5,4x4 |
4,9, |
||
|
|
||||
|
11x3 |
14x4 |
12,5. |
|
|
|
|
||||
3-й шаг. Вычисляя множитель 43 ( 11) /( 4,4) 2,5 и вычитая из четвертого уравнения системы (4.12) третье уравнение, умноженное на
43, приводим систему к треугольному виду:
10x1 |
6x2 |
|
2x3 |
25, |
|
|
2x2 |
|
3x3 4x4 |
1,5, |
|
|
(4.13) |
||||
|
4,4x3 5,4x4 |
4,9, |
|||
|
|
||||
|
|
|
0,5x4 0,25. |
|
|
|
|
|
|
||
