
8116
.pdf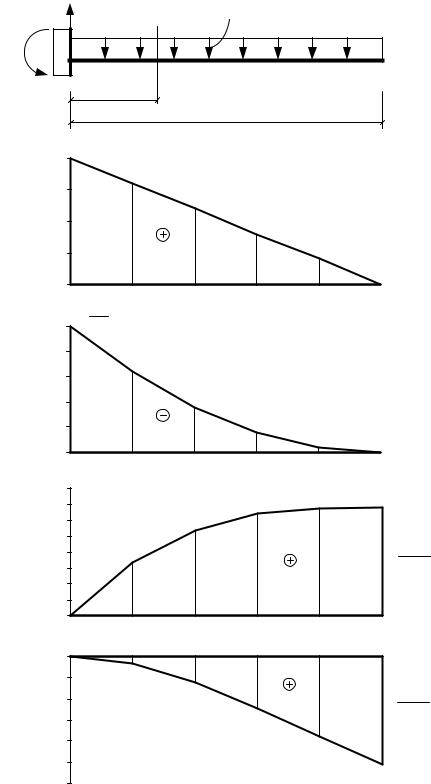
R = 20кН
q = 20 кН/м
|
z |
|
l = 1м |
|
q l |
20 |
эп.Qy |
|
|
15 |
|
10 |
|
5 |
|
0 |
|
|
q l 2 |
-10 |
2 |
эп.Мх |
|
|
|
-8 |
|
|
-6 |
|
|
-4 |
|
|
-2 |
|
|
0 |
|
|
0,004 |
эп. |
|
|
||
0,0035 |
|
|
0,003 |
|
|
0,0025 |
q l3 |
|
0,002 |
||
|
||
0,0015 |
6 E J |
|
0,001 |
|
|
0,0005 |
|
|
0 |
|
|
0 |
|
|
0,5 |
|
|
1 |
q l 4 |
|
|
||
1,5 |
8 E J |
|
|
||
2 |
|
|
2,5 |
эп.V |
|
|
||
3 |
|
|
|
Рис.1.6 |
Пример 1.2. Подобрать сечение стальной балки (рис. 1.7) из прокатного двутавра. Расчётные характеристики балки: [ σ ] = 160 МПа, [ τ ] = 100 МПа, Е = 2٠105 МПа.
Длина пролёта балки l = 6 м. Допускаемый прогиб [ f ] = l / 400 = 6000 мм / 400 = 15 мм.
1. Определяем размеры прокатного двутавра из условия прочности балки на изгиб.
Wx ³ |
M |
= |
8000 кНсм |
= 500 см3 . |
x |
|
|||
[σ ] |
16 кН / см3 |
Из таблицы 1. Сталь горячекатанная. Балки двутавровые (ГОСТ 8239-72*) находим сле-
дующий номер профиля: |
|
|
|
|
|
Двутавр №30а: Wx = 518 см3, |
Jx = 7780 см4, S*x = 292 см3, d = 0,65 см. |
||||
2. Выполняем проверку балки на срез. |
|
|
|||
τ = |
|
Q S*x |
£ [τ ], |
|
|
|
y |
|
|
||
|
|
|
|
|
|
|
|
J x d |
|
|
|
τ = |
|
40 кН ×292см3 |
|
= 2,3кН / см2 = |
|
|
|
|
|
||
|
7780см4 ×0,65см |
||||
=23 МПа << [τ ] = 100 МПа.
3.Определяем жёсткость балки при изгибе.
EJx = 2٠104 кН/см2× 7780 см4 = 15560 ٠104 кНсм2 = 15560 кНм2 .
4. Балка имеет 2 участка (рис. 1.7).
Составляем дифференциальное уравнение для каждого участка и дважды интегрируем. Начало координат помещаем на левом конце балки. Ось у направляем вниз.
I участок. 0 < z < 4 м |
II участок. 4 м < z < 6 м |
|
|
EJx v1 // = - Мх = - (20 z) |
EJx v2 // = - Мх = - (20 z – 60 (z-4)) |
EJx θ1 = - 10 z2 + C1 |
EJx θ2 = - 10 z2 + 30 (z-4)2 + C2 |
|
|
EJx v1 = - (10/3) z3 + C1 z + D1 |
EJx v2 = - (10/3) z3 + 10 (z-4)3 + C2 z + D2 |
|
|
5. Определяем постоянные интегрирования.
· Условие плавности изогнутой оси при z = 4 м: θ1 (4) = θ 2 (4). Отсюда находим С1 = С2.
·Условие непрерывности изогнутой оси z = 4 м: v1 (4) = v 2 (4). Отсюда находим D1 = D2.
·Условие закрепления балки при z = 0: v1(0) = vA = 0. Отсюда находим D1 = D2 = 0.
·Условие закрепления балки при z = 6 м: v2(6) = vВ = 0. Отсюда находим С1 = С2 = 320/3.
С учётом полученных значений постоянных интегрирования для углов поворота и прогибов сечений балки окончательно получаем следующие выражения:
I участок. 0 < z < 4 м |
II участок. 4 м < z < 6 м |
||
|
|
|
|
EJx θ1 |
= - 10 z2 + 320/3 |
EJx θ2 |
= - 10 z2 + 30 (z-4)2 + 320/3 |
|
|
|
|
EJx v1 |
= - (10/3) z3 + (320/3) z |
EJx v2 |
= - (10/3) z3 + 10 (z-4)3 + (320/3) z |
|
|
|
|
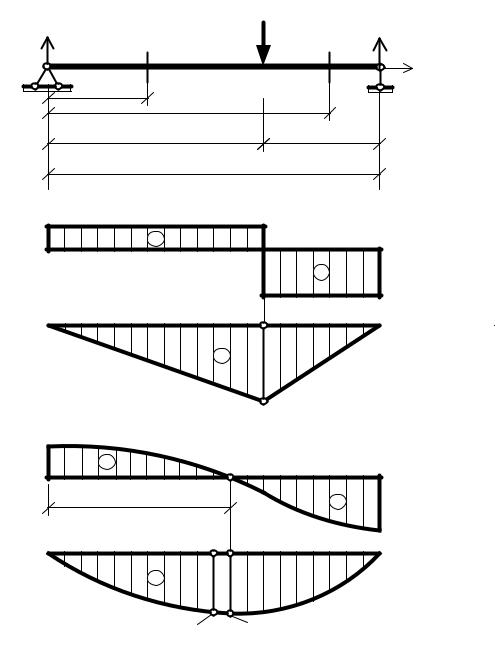
Эпюры углов поворота и прогибов балки показаны на рис. 1.7.
Максимальный прогиб в сечении балки 1 участка, где θ1 = 0:- 10 z2 + 320/3 = 0.
Отсюда находим координату сечения z ≈ 3,266 м.
Максимальный прогиб в этом сечении будет равен f ≈ 14,93 мм.
Прогиб в середине пролёта балки при z = 3 м равен vсер. ≈ 14,78 мм.
Максимальный прогиб и прогиб в середине пролёта отличаются всего лишь на 1%, поэтому при проверке балок на жёсткость достаточно определить прогиб в середине пролёта.
Рис. 1.7
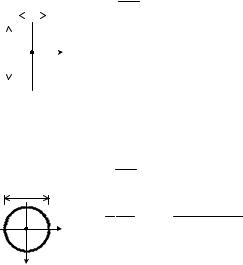
Пример 1.3. |
Выполнить расчёт деревянных балок с прямоугольным и круглым сечением. |
||||||||||||
Расчётные характеристики балок: [ σ ] = 12 МПа, [ τ ] = 2 МПа, Е = 104 МПа, |
[ f ] = l/200. |
||||||||||||
1.Определяем размеры поперечного сечения балок. |
|
|
|
||||||||||
|
|
|
|
|
|
Балка с прямоугольным поперечным сечением. |
|
||||||
|
|
|
|
Mx |
|
b×4b2 |
|
6125кНсм |
3 |
|
|
||
|
b |
|
Wx ³ |
[σ ] |
; |
Wх = |
|
³ |
|
= 5104,2см |
|
. b = 19, 7 см ≈ 20 |
см. h = 40 см. |
|
|
6 |
1,2кН / см2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
h=2b |
|
|
x |
||
|
|
|
|
||
|
|
|
|
|
|
 y
y
d |
x |
y |
τ = |
3 Qу |
|
|
|
70кН |
|
|
2 |
|
< [τ ]=2МПа. |
|||||
|
|
|
|
= 1,5× |
|
|
= 0,13 |
кН /см |
|
= 1,3МПа |
|||||
2 |
А |
(20×40)см2 |
|
||||||||||||
Jx = |
bh3 |
= |
20×403 |
= 106667см4 . |
EJx = 103 кН/см2 · 106667 см4 = 10666,7 кНм2. |
||||||||||
|
|
||||||||||||||
|
12 |
|
|
12 |
|
|
|
|
|
|
|||||
Wx ³ M[σx];
τ= 4 Qу
3 А
Балка с круглым поперечным сечением.
|
Wх |
= π ×d3 |
³ |
6125кНсм |
= 5104,2см3 . d = 37,3 см ≈ 40 см. |
|||||
|
2 |
|||||||||
|
|
|
|
32 |
|
1,2кН / см |
|
|
||
|
4 |
|
|
70кН |
|
|
кН /см2 = 0,74МПа < [τ ]=2МПа. |
|||
= |
|
|
|
× |
(π ×202 )см2 |
= 0,074 |
||||
3 |
|
|||||||||
Jx = π d4 |
= π ×404 |
= 125664см4 . EJx = 103 кН/см2 · 125664 см4 = 12566,4 кНм2. |
64 |
64 |
|
2. Определяем перемещения балки. Начало координат помещаем на границе участков
(рис. 1.8). Ось у направляем вниз.
1 участок. 0 < z < 4 м |
|
|
2 участок. 0 < z < 2 м |
|
|
||
|
|
|
|
|
|
||
Q1x = 70 – 40 z |
|
Q2x = 70 – 40 ·4 + 120 = 30 кН |
|||||
M1х = 70 z – 20 z2 |
|
M2х = -20+ 70(4+z)- 40·4(2+z)+ 120z = -60 + 30z |
|||||
EJxv1// = - М1х = - 70 z + 20 z2 |
|
EJxv2// = - М2х = 60 – 30 z |
|
|
|||
EJxθ1 = - 35 z2 + 20/3 z3 + C1 |
|
EJxθ2 |
= 60 z – 15 z2 + C2 |
|
|
||
EJxv1 = - 35/3 z3 + 5/3 z4 + C1 z + D1 |
|
EJxv2 |
= 30 z2 – 5 z3 + C2 z + D2 |
||||
3. Постоянные интегрирования определяем из следующих условий: |
|
|
|||||
|
|
|
|
|
|
|
|
Условие закрепления на опоре А: |
|
|
z1 |
= 0 |
v1(0) |
= 0 |
|
Условие плавности на границе участков: |
z1 |
= 4 м, z2 = 0 |
θ1(4) = θ2 (0) |
|
|||
Условие непрерывности на границе участ- |
z1 |
= 4 м, z2 = 0 |
v1(4) |
= v2 (0) |
|
||
ков: |
|
|
|
|
|
|
|
Условие закрепления на опоре В: |
|
|
z2 |
= 0 |
v2(0) |
= 0 |
|
В результате получим следующие значения для постоянных интегрирования: |
|||||||
D1 = 0, |
D2 = 0, |
C1 = 80, C2 = - 53,33. |
|
|
|||
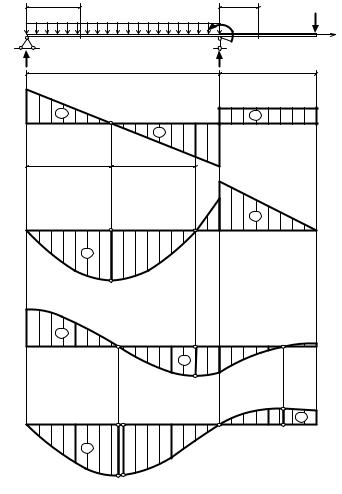
4. Вычисляем перемещения в сечениях балок и строим эпюры перемещений.
z1 (м) |
0 |
1 |
2 |
3 |
|
4 |
|
-+++++---- |
|
|
|
|
|
|
|
|
|
z2 (м) |
|
|
|
|
|
0 |
1 |
2 |
|
|
|
|
|
|
|
|
|
EJxθ |
80,00 |
51,67 |
- 6,67 |
-55,00 |
|
-53,33 |
-8,33 |
6,67 |
EJxv |
0,00 |
70,00 |
93,33 |
60,00 |
|
0,00 |
- 28,33 |
- 26,66 |
|
|
|
|
|
|
|
|
|
|
|
|
Прямоугольная балка |
|
|
|
||
|
|
|
|
|
|
|
|
|
θ (рад) |
0,00750 |
0,00484 |
- 0,00063 |
- 0,00516 |
|
- 0,00500 |
- 0,00078 |
0,00063 |
v (мм) |
0,00 |
6,56 |
8,75 |
5,63 |
|
0,00 |
- 2,66 |
- 2,50 |
|
|
|
|
|
|
|
|
|
|
|
|
Круглая балка |
|
|
|
||
|
|
|
|
|
|
|
|
|
θ (рад) |
0,00637 |
0,00411 |
- 0,00053 |
- 0,00438 |
|
- 0,00424 |
- 0,00066 |
0,00053 |
v (мм) |
0,00 |
5,57 |
7,43 |
4,78 |
|
0,00 |
- 2,25 |
- 2,12 |
|
|
|
|
|
|
|
|
|
5. Проверяем условие жёсткости балок:
Прямоугольная балка - v = 8,75 мм < [ f ] = 4000 мм / 200 = 20 мм.
Круглая балка - v = 7,43 мм < [ f] = 4000 мм / 200 = 20 мм.
Таким образом, полученные из условий прочности размеры поперечного сечения балок обеспечивают также выполнение условий жёсткости балок.
Рис. 1.8 |
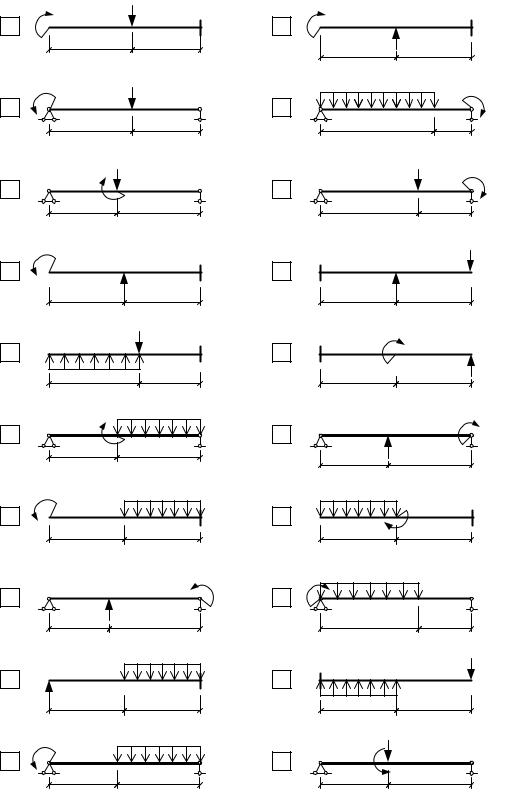
На рис.1.9 приведены задачи для самостоятельного решения методом непосредственного интегрирования по участкам. Подобрать сечение стальной балки из прокатного двутавра.
Расчётные характеристики балок: [ σ ] = 160 МПа, [ τ ] = 100 МПа, Е = 2٠105 МПа. Допускаемый прогиб [ f ] = l / 100, где l – длина балки.
Рис. 1.9
1.2.Метод начальных параметров
1.2.1Основные положения метода
Существует метод: метод начальных параметров, который позволяет свести решение к определению всего двух постоянных интегрирования. Для этого необходимо при решении использовать приём, который сводится к следующим правилам:
∙При решении задачи использовать единую (глобальную) систему координат для всех участков балки. Начало координат необходимо помещать на левом или правом конце балки.
∙Жесткость всех участков балки должна быть одинаковой и постоянной – EJx = const.
∙Прогиб и угол поворота в начале координат обозначим vo и θо, которые называются геометрическими или кинематическими начальными параметрами.
∙Изгибающий момент и поперечную силу в начале координат обозначим Mo и Qо, которые называются статическими начальными параметрами.
∙При составлении выражения изгибающего момента для нагрузки от сосредоточенных моментов необходимо использовать следующую форму записи: M = M(z-a)o.
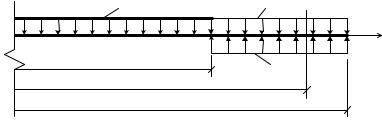
∙Если распределённая нагрузка обрывается в сечении, расположенном левее сечения с абсциссой z (ось z направлена вправо), необходимо нагрузку продолжить до конца балки и одновременно приложить на этой части балки такую же нагрузку, но противоположного направления (рис. 1.10).
Рис. 1.10
∙ При интегрировании двучленов вида (z-a)k следует пользоваться следующей форму-
лой |
|
|
k+1 |
|
= |
(z − a) . |
|||
∫(z − a)k dz |
||||
|
|
k + 1 |
|
|
Как будет показано в следующем параграфе, при соблюдении этих правил,
произвольные постоянные интегрирования на всех участках получаются одинаковыми, и
решение задачи сводится к нахождению лишь двух неизвестных при любом числе участков статически определимой балки.
1.2.2 Универсальное уравнение прогибов и углов поворота.
Рассмотрим балку постоянного сечения, нагруженную моментом M, cосредоточенной силой F и распределёнными нагрузками (рис. 1.11). Ось z направим вправо. Направление на-
грузок создают положительные изгибающие моменты. Рассматриваемая балка имеет четыре

участка, каждому из которых соответствует свое уравнение моментов, уравнение прогибов и |
углов поворота сечений. |
Рис. 1.11 |
Для балки постоянного сечения дифференциальное уравнение записываем в виде |
EJxv′′(z) = ± Mx (z). |
(1.6) |
|
Напоминаем, что в уравнении (1.6) выбираем знак «плюс», если ось у направляем
вверх, и знак «минус», если ось у направляем вниз. Для каждого участка балки (рис. 1.11) со-
ставляем дифференциальное уравнение изогнутой оси и дважды его интегрируем, применяя правила, изложенные в пункте 1.2.1.
1-й участок. 0 ≤ z ≤ а: EJx v1′′ (z) = ± Mx(1) (z) = ± [Mo + Qo z].
2-й участок. a ≤ z ≤ b:
3-й участок. b ≤ z ≤ c:
EJ |
θ |
|
(z) = ± |
M z + Q |
z2 |
+ C |
|
. |
|
||||||||
1 |
|
|
|
|
1 |
|
|||||||||||
x |
|
|
|
o |
|
o |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
EJ |
v |
|
(z) = ± |
M |
z2 |
+ Q |
|
z3 |
+ C |
|
z + D . |
||||||
1 |
|
|
|
|
|
|
1 |
||||||||||
x |
|
|
|
o |
|
o |
|
|
|
|
|
1 |
|||||
|
|
|
|
|
|
2 |
|
|
|
6 |
|
|
|
|
|
|
|
EJx v2′′ ( z ) = ± M x(2) (z ) = ± Mo + Qo z + M (z − a )o .
|
|
|
|
z2 |
|
|
|
|
|||||
EJxθ 2 |
( z ) = ± Mo |
z + Qo |
|
|
|
+ M (z − a ) |
+ C2 . |
|
|||||
|
|
|
|
||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
||
|
|
z2 |
|
z3 |
( z − a )2 |
|
|
||||||
EJx v2 |
(z ) = ± Mo |
|
+ Qo |
|
|
|
+ M |
|
|
+ C |
2 z + D2 |
||
2 |
6 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJx v3′′ ( z ) = ± M x(3 ) ( z ) = ± M o + Qo z + M ( z − a )o + F ( z − b ) .
|
|
|
|
z 2 |
|
( z − b )2 |
|
|
|
|||
EJxθ 3 |
( z ) = ± M o |
z + Qo |
|
|
+ M ( z − a ) + |
F |
|
+ C 3 . |
|
|||
|
|
|
||||||||||
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 2 |
|
z 3 |
( z − a )2 |
( z − b )3 |
|
|
||||
EJx v3 |
( z ) = ± M o |
|
+ Qo |
|
|
+ M |
+ F |
|
|
+ C |
3 z + D3 . |
|
|
|
|
|
|||||||||
|
|
2 |
|
|
6 |
2 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.7)
(1.8)
(1.9)

4-й участок. c ≤ z ≤ l: |
|
4 |
|
|
|
|
|
+ Qo z + M |
(z − a) |
o |
+ F (z − b) + q |
(z − c)2 |
+ tgα |
(z − c)3 |
|
|||||||
EJx v4′′ (z) = ± Mx( |
|
) (z) = ± Mo |
|
2 |
|
|
|
6 |
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
(z − b)2 |
(z − c)3 |
|
(z − c)4 |
|
|
|
|||||||
|
|
|
|
|
z2 |
|
|
|
|
|
||||||||||||
EJxθ4 |
(z) = ± Mo |
z + Qo |
|
|
|
+ M (z − a) + F |
|
+ q |
+ tgα |
|
|
|
+ C4 . |
(1.10) |
||||||||
|
2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
6 |
|
|
24 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
z3 |
(z − a)2 |
(z − b)3 |
(z − c)4 |
|
(z − c)5 |
|
|
|||||||||
EJx v4 |
(z) = ± Mo |
|
+ Qo |
|
|
|
+ M |
+ F |
|
|
+ q |
+ tgα |
|
|
|
+ C4 z + D4 . |
||||||
2 |
6 |
|
6 |
120 |
||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
24 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Изогнутая ось балки есть плавная кривая. На границах участков балки значения углов
поворота и прогибов, вычисленных из уравнений соседних участков, будут равны. Эти ра-
венства называются условиями плавности и непрерывности изогнутой оси на границе участ-
ков (рис. 1.11).
Рассмотрим эти условия, используя полученные для балки выражения (1.7) ÷ (1.10).
Граница 1-го и 2-го участков. z = a: |
θ1(a) = θ2(a). |
Отсюда следует С1 = С2. |
|
|
v1(a) = v2(a). |
Отсюда следует D1 |
= D2. |
Граница 2-го и 3-го участков. z = b: |
θ2(b) = θ3(b). |
Отсюда следует С2 = С3. |
|
|
v2(b) = v2(b). |
Отсюда следует D2 |
= D3. |
Граница 3-го и 4-го участков. z = c: |
θ3(c) = θ4(c). |
Отсюда следует С3 |
= С4. |
|
v3(c) = v4(c). |
Отсюда следует D3 = D4. |
|
Из полученного решения следует, что, используя при решении правила, изложенные в пункте 2.1, постоянные интегрирования всех участков балки всегда будут равны и могут
быть заменены фактически двумя постоянными интегрирования независимо от количества участков балки:
С1 = С2 = С3 = С4 = ….. = С. D1 = D2 = D3 = D4 = ….. = D. (1.11)
С учётом введённых обозначений угла поворота и прогиба в начале координат (п. 2.1) из
равенств (2.3) при z = 0 получим следующие выражения постоянных интегрирования С и D:
C = EJxθo, D = EJxvo, |
(1.12) |
т.е. постоянная интегрирования С есть угол поворота в начале координат, |
а D – прогиб в |
начале координат, умноженные на жёсткость балки при изгибе. |
|
Из формул (2.6) следует, что выражения моментов, углов поворота и прогибов преды-
дущих участков входят как составная часть выражений для последнего (4-го ) участка балки.
Это позволяет результаты решения для всех участков объединить и записать формулы для углов поворота и прогибов в виде единого выражения для всех участков, используя сле-
дующий приём:
|
k |
|
0 |
при z £a |
|
|
|
|
z³a (z - a) |
|
|
|
(1.13) |
||||
|
= |
|
|
|
|
. |
||
|
(z - a) |
k |
при z |
|
||||
|
|
|
|
³a |
|
|||
|
|
|
|
|
|
|
|
|
Применяя правило (2.9), из формулы для погибов 4-го участка (2.6) при z < a получим выражение прогиба 1-го участка, при z < b получим выражение прогиба 2-го участка,
при z < c получим выражение прогиба 3-го участка.
Таким образом, для уравнения прогибов балки с учётом (2.7) и (2.8) можно записать обобщённое уравнение прогибов в виде:
EJxv(z) = EJxvo |
|
2 |
|
3 |
+ M (z−a) |
2 |
+ F (z−b) |
3 |
+ q (z−c) |
4 |
+tgα (z−c) |
5 |
|
|
+ EJxθoz ± Mo |
z |
+ Qo |
z |
|
|
|
|
|
(1.14) |
|||||
2 |
6 |
|
|
|
|
|||||||||
|
|
|
2 |
|
6 |
|
24 |
|
120 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение (1.14) является универсальным уравнением прогибов балки,
поскольку может быть использовано для определения прогибов для балки с любым числом участков.
Определение прогибов балок с помощью универсального уравнения (1.14) требует выполнения следующих правил.
1.Уравнение (1.14) применимо для решения балок только с постоянной жёсткостью:
EJx = const.
2.Начало координат необходимо помещать либо на левом конце балки, либо на правом конце балки.
3.Знак «плюс» перед квадратными скобками следует выбирать, если ось у направить вверх, а знак «минус», если ось у направить вниз.
4.Прогиб балки всегда выражается через четыре начальных параметра: два статических Мо, Qo и два геометрических vo, θo, поэтому метод называется методом начальных параметров.
5.Неизвестный прогиб vo и угол поворота θo в начале координат необходимо определять из условий закрепления балки (рис.1.11). В частности:
∙ |
если в начале координат расположена жёсткая заделка, то |
vo = 0 |
и |
θo = 0; |
∙ |
если в начале координат расположена шарнирная опора, то |
vo = 0 |
и |
θo ≠ 0; |
∙ |
если в начале координат отсутствует опора (свободный край), то |
vo ≠ 0 и θo ≠ 0. |
||
6.При использовании универсального уравнения условия плавности и непрерывности на границах участков балки выполняются автоматически.
7.Знак слагаемых, стоящих в квадратных скобках, определяют по правилу знаков для изги-
бающих моментов. В частности:
∙если силы F и нагрузки q направлены вверх, то изгибающие моменты от такой нагрузки будут положительными независимо от выбора положения начала координат;
∙если силы F и нагрузки q направлены вниз, то изгибающие моменты от такой нагрузки будут всегда отрицательными;
