8062

Для стержней, не имеющих ослабления поперечного сечения, достаточно производить только расчёт на устойчивость. Если стержень имеет местное ослабление поперечного сече-

ния, расчёт на устойчивость необходимо дополнить расчётом на прочность в ослабленном сечении по известной формуле:

В заключение следует отметить, что рациональными являются те поперечные се-

чения, у которых моменты инерции относительно главных центральных осей близки по значению или даже равны. Стойки, имеющие такое сечение, обладают равноустой-

чивостью во всех направлениях. Указанным требованиям удовлетворяет кольцевое сечение. Часто применяют также сечения, составленные из прокатных профилей, распо-

ложенных таким образом, что все главные моменты инерции полученного составного сечения одинаковы.

Пример 1.

Стержень, показанный на рис. а сжимается силой F = 600 кН. Сечение стержня, состоящее из двух равнобоких уголков, изображено на рис. б. Материал стержня – сталь С235 с

допускаемым напряжением Требуется подобрать размеры уголков так, чтобы выполнялись условия устойчивости и прочности и расход материала был минимальным. Ослабления составляют 15% площади сечения.

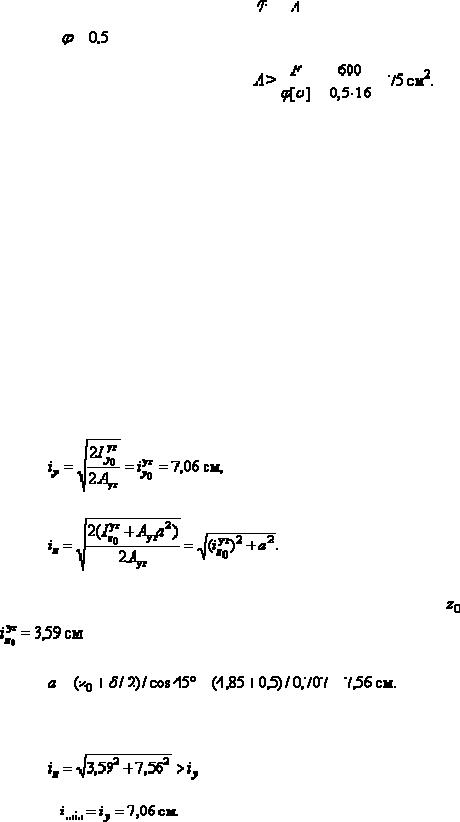
Решение.

Сечение стержня состоит из уголков (прокатного профиля), поэтому используем для

подбора сечения метод последовательных попыток. Поскольку в условии устойчивости име-

ем сразу две неизвестные величины ( и ), то одной из них задаемся произвольно. Удобно

Площадь одного уголка Ауг ≥ 37,5 см2. Из сортамента прокатной стали выбираем уголок, удовлетворяющий этому условию. Отметим, что в сортаменте может быть несколько уголков с примерно одинаковой площадью: уголки с длинной полкой и тонкой стенкой и уголки с короткой, но более толстой стенкой. Выбирать следует самые тонкие уголки, т.к.

при одинаковой площади радиус инерции у тонких уголков больше и, следовательно, гиб-

кость стержня с сечением из тонкого уголка меньше, а чем меньше гибкость, тем более ус-

тойчив стержень. В рассматриваемом примере выберем уголок 180х11, площадь которого Ауг = 38,8 см2. Найдем радиусы инерции относительно главных центральных осей y и z, кото-

рыми являются оси симметрии сечения (см. рис. б). Следует ожидать, что радиус инерции относительно оси y будет минимальным, так как материал ближе расположен к оси y, чем к оси z. Убедимся в этом.

Таким образом, очевидно, что

и

Теперь найдем гибкость стержня (заметим, что, если в сортаменте выбрать уголок с более толстой полкой, но с примерно такой же площадью, например, уголок 160×12 (Ауг =

37,4 см2), минимальный радиус инерции сечения из двух таких уголков будет imin = 6,23 см и гибкость стержня будет на 13% больше, чем для уголка 180×11).

и из таблицы, интерполируя, найдем . Проверим условие устойчивости

Условие устойчивости выполняется, но сечение не является экономичным. Поэтому сделаем еще попытку. Уменьшим размеры сечения и примем самый тонкий уголок их тех, у

которых длина полки 160 мм, а именно, уголок 160×10. 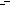, и гибкость стержня

По таблице (справочные данные) находим и условие устойчивости выполняется с небольшим запасом:

Сечение из двух уголков 160×10 можно считать экономичным. Условие прочности для подобранного сечения тоже выполняется, поскольку согласно условию

.

В заключение найдем действительный коэффициент запаса устойчивости. Поскольку

в пределах между и , то определяем критическую силу по формуле Ясинского

Действительный коэффициент запаса устойчивости

Пример 2.

Стальной стержень длиной сжимается силой .

Требуется:

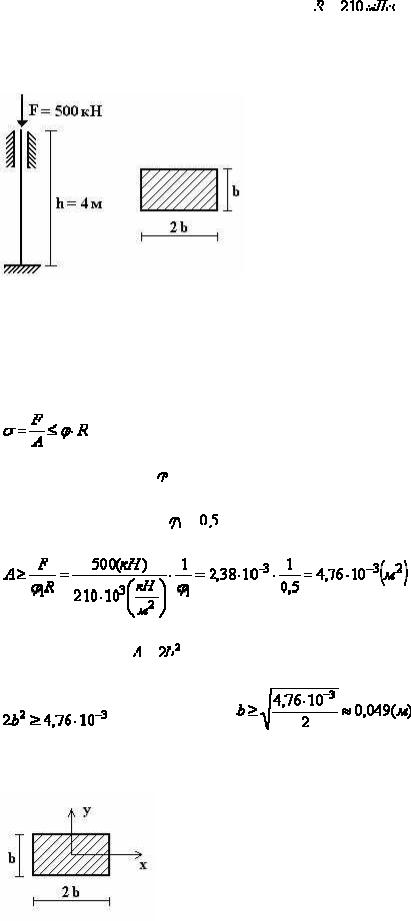
1.Найти размеры поперечного сечения при с помощью метода последовательных приближений;

2.Найти значение критической силы и коэффициент запаса устойчивости.

Решение.

1) В условии устойчивости

неизвестны величины и А.

В первом приближении

С другой стороны

. Следовательно,

Определим минимальный радиус инерции

Коэффициент приведения длины , согласно для данного типа закрепления равен

0,5.

Гибкость стержня

По таблице из справочника (коэффициенты φ продольного изгиба центрально сжатых элементов по СНиП II 23 – 81) находим

при

при

при

Интерполяцией определяем

Сравниваем

Проверка:

Считаем напряжения

61% > 5%

Во втором приближении принимаем

при

при

Сравниваем

Проверка:

8% > 5%

В третьем приближении

при

при

Сравниваем

Проверка:

0,3% < 5%

Полученное значение близко к принятому, поэтому окончательно

2) Найдем значение критической силы и коэффициент запаса устойчивости.

,

значит применима формула Эйлера.

Коэффициент запаса устойчивости

6. Оценка прочности при ударной нагрузке.

Вид формул, полученных для динамического коэффициента, показывает, какие большие

качественные различия ведет за собой количественное изменение периода действия силы на тело.

Рассмотрим некоторые случаи удара при простейших деформациях. При этом для нахо-

ждения коэффициента динамичности применим основные полученные формулы для дина-

В случае продольного растягивающего или сжимающего удара (Рис 6.1)

Рис. 6.1 Модель продольного удара.

Для вычисления динамического коэффициента может быть выбрано одно из сле-

дующих выражений:

После этого без затруднений вычисляются , и .

Приближенная формула для вычисления напряжений в данном частном случае получает

такой вид:

и

Замечаем, что как при статической, так и при динамической нагрузке напряжение в сжа-

том стержне зависит от величины сжимающей силы и от площади поперечного сечения

стержня.

Но при статическом действии груза Q передающаяся на стержень сила равна Q и не зави-

сит от размеров и материала стержня, при ударе же величина силы , вызывающей напря-

жения в стержне, зависит от ускорения, передающегося от ударяемого тела на ударяющее, т.

е. от величины промежутка времени, в течение которого изменяется скорость ударяющего тела. В свою очередь этот промежуток времени зависит от величины динамической продоль-

ной деформации , от податливости стержня. Чем эта величина больше, т. е. чем меньше

модуль Е и чем больше длина стержня l, тем больше продолжительность удара, меньше ус-

корение и меньше давление .

Таким образом, при равномерном распределении напряжений, одинаковом во всех сече-

ниях стержня, динамическое напряжение будет уменьшаться с увеличением площади попе-

речного сечения стержня и с увеличением его податливости (т. е. с увеличением длины и уменьшением модуля упругости Е); именно поэтому смягчают удар всякие рессоры и пру-

жины, расположенные между ударяющимися деталями. Все это и отражают приведенные выше формулы. В частности, с известным приближением можно считать, что при продоль-

ном ударе величина напряжений зависит уже не от площади, а от объема стержня.

Вычислив величину динамического напряжения, мы можем теперь написать условие прочности в виде

где [ ]— допускаемая величина нормальных напряжений при ударе, равная для пла-

равной величине основного коэффициента запаса при статическом действии нагрузок, так как динамичность нагрузки уже отражена. Однако, ввиду некоторой упрощенности изложен-

ного метода расчета, этот коэффициент принимают несколько повышенным — до 2. Кроме того, обычно в этих случаях применяют материал более высокого качества (в отношении од-

нородности и пластических свойств).

При изгибе величина статической деформации , представляющей собой статический прогиб балки с в месте удара, зависит от схемы нагружения и условий опирания балки.

Так например, для балки пролетом l, шарнирно закрепленной по концам и испытываю-

щей посредине пролета удар от падающего с высоты Н груза Q (рис.6.2, а), получаем:

для консоли, испытывающей удар от груза Q, падающего на свободный конец консоли

(Рис 6.2, б):

.

Рис. 6.2 Модель удара: а) двухопорная балка, б) консольная Подставляя в формулу для коэффициента динамичности значения или ,

находим , а затем и величину динамических напряжений и деформаций. Так например, в

случае балки на двух опорах при вычислении динамического напряжения имеем такую формулу:

Условие прочности в этом случае напишется: