
7700
.pdf
Условие непрерывности функции |
y в точке |
x2 1 выполняется, |
|||||
значит, функция y в точке x2 1 непрерывна. |
|
||||||
Построим график функции y : |
|
|
|
|
|||
|
|
y |
y x2 |
|
|||
1 |
|
|
|
|
|
||
|
|
|
|
|
|||
0 |
|
1 |
2 |
|
x |
||
y |
1 |
|
|
|
|
|
y 2 x |
x |
|
|
|
||||
|
|
|
|
|
|||
Рис. 54
Производная
Пусть функция y f x определена на некотором интервале a;b .
Аргументу |
x a;b |
дадим |
приращение |
x , получим точку |
||||||||||
x x a;b . |
Найдем |
соответствующее |
приращение |
функции: |
||||||||||
y f x x f x . |
Составим отношение приращения |
y |
функции |
|||||||||||
y к приращению x аргумента |
x : |
y |
и найдем предел этого отношения |
|||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
при x 0, то |
есть |
lim |
y |
. Если |
этот |
предел |
существует, то |
его |
||||||
|
|
|
x 0 |
x |
|
|
|
|
|
|
|
|
|
|
называют |
производной |
функцией |
от |
данной |
функции |
y f x |
и |
|||||||
обозначают одним из символов: |
|
|
dy |
, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||||||
y x , |
|
f x , |
yx . |
|
|
|
||||||||
dx
Итак, по определению
20
|
|
y x x y x |
. |
||
|
|
|
|
||
y x lim |
|
x |
|||
|
x 0 |
|
|
||
|
|
|
|
|
|
Функция y f x , |
имеющая |
производную в каждой точке |
|||
интервала a;b , называется дифференцируемой в этом интервале, а
операция |
нахождения |
производной |
функции |
называется |
||||
дифференцированием. |
|
|
|
|
|
|
|
|
Значения производной |
функции |
|
y f x |
|
|
в |
точке x x0 |
|
обозначается одним из символов: y x0 , |
f x0 или |
y |
|
x x0 . |
||||
|
||||||||
Пример. Найти по определению производную функции y x2 .
Решение. Областью определения D данной функции является вся числовая ось, то есть D R . Выберем произвольную точку x R . Дадим
ей приращение x , получим новую |
точку x x R . Находим |
соответствующее приращение y функции |
y x2 : |
y y x x y x x x 2 x2
x2 2x x x 2 x2 2x x x 2 .
Составим отношение |
y |
|
2x x x 2 |
2x x |
и найдем предел |
|
x |
x |
|||||
|
|
|
|
|||
отношения при x 0: |
|
|
|
|
||
lim |
y lim 2x x 2x 0 2x . |
|
||||
x 0 |
x |
x 0 |
|
|
||
Поскольку данный предел существует, то производная функции y x2 в
точке x равна 2x , то есть x2 2x .
Пусть материальная точка (тело) движется неравномерно по закону прямолинейного движения S S t . Каждому значению истекшего времени t соответствует определенное расстояние S до некоторой фиксированной точки O . Тогда средняя скорость Vcp движения точки за время t равна:
21

Vcp St , где S S t t S t .
Предел средней скорости Vcp движения при стремлении к нулю
промежутка времени t называется скоростью V движения точки в данный момент времени (или мгновенной скоростью)
V lim S .
t 0 t
Таким образом, скорость прямолинейного движения материальной точки в момент времени t есть производная от пути S по времени t , то есть
V St . В этом заключается механический смысл производной. |
|||
Если функция y f x описывает какой-либо физический процесс, |
|||
то производная y есть |
скорость протекания этого процесса. В этом |
||
состоит физический смысл производной. |
|
|
|
y |
|
y f x |
|
|
|
|
|
|
n |
M x; y |
|
|
|
|
|
|
|
y |
l |
|
M 0 |
A |
|
|
x |
|
|
|
|
|
|
0 |
x |
|
|
0 |
x0 |
Рис. 55 |
x |
|
|
|
|
Под касательной l к графику функции y f x в точке M 0 понимают
предельное положение секущей M 0 M , когда |
точка M движется по |
|
кривой к точке M 0 (см. рис. 55). |
Нормалью |
n называется прямая, |
проходящая через данную точку M 0 |
перпендикулярно касательной l (см. |
|
рис. 55). |
|
|
22

Пусть касательная l образует с положительным направлением оси
Ox угол 0 , а секущая M 0 M – угол x . Тогда из прямоугольного треугольника AM 0 M , получаем: tg x yx . Переходя к пределу при
x 0, находим:
lim tg x lim |
y |
y x0 tg 0 k , |
||
x 0 |
x 0 |
x |
|
|
|
|
|
в точке |
x0 равна угловому коэффициенту k |
То есть производная y x0 |
||||
касательной l |
к графику функции |
y f x в точке, абсцисса которой |
||
равна x0 . В этом заключается геометрический смысл производной.
Пользуясь уравнением прямой, проходящей через заданную точку M 0 x0 ; y0 в заданном направлении y y0 k x x0 , запишем уравнение касательной l к графику функции y f x в точке M 0 x0 ; y0
:
y y0 y x0 x x0 .
Поскольку нормаль n перпендикулярна касательной l , то ее угловой
коэффициент kn
кривой y f x
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
. |
Поэтому уравнение нормали n к |
||||
kl |
y x0 |
|||||||||
в точке |
M 0 x0 ; y0 |
имеет вид: |
||||||||
|
y y0 |
|
1 |
|
|
x x0 . |
||||
|
|
|
|
|
||||||
|
y x0 |
|||||||||
|
|
|
|
|
|
|
||||
Пример. Составить уравнение касательной и нормали к кривой y x2 в точке M 0 1;1 .
Решение. Поскольку x2 2x , то
y x0 2x x 1 2 1 2
и искомое уравнение касательной:
y 1 2 x 1 или y 1 2x 2,
23

откуда 2x y 1 0, а искомое уравнение нормали:
y 1 |
1 |
x 1 или 2y 2 x 1, |
|
2 |
|||
|
|
откуда
x 2y 3 0.
Нахождение производной функции непосредственно по определению часто связано с некоторыми трудностями. На практике функции дифференцируют с помощью правил и формул.
Запишем формулы производных элементарных функций:
|
|
|
|
const ; |
|
|
n |
xn 1 , |
|
|
n R , n 0 ; |
|||||||||||||||||||
c 0 , c |
|
xn |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 , a 1; |
|
|
ex ; |
|
|
|
|
||||||||
ax ax ln a , a |
|
ex |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
log a x |
|
|
|
|
|
|
|
|
|
|
, a 0 , a 1; |
ln x |
|
|
; |
|
|
|||||||||||||
|
x ln a |
x |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x ; |
|
|
|
|
|
|
|
|
|
|
|||||
sin x |
|
cos x ; cos x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
tg x |
|
|
|
|
|
|
; ctgx |
|
|
|
|
; |
|
|
|
|
|
|
|
|||||||||||
cos2 |
x |
sin 2 |
x |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||
arcsin x |
|
|
|
|
|
; arccos x |
|
|
|
|
|
; |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1 x2 |
|
1 x2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
arctg x |
|
|
|
; |
arcctg x |
|
|
; |
|
|
|
|||||||||||||||||||
1 x2 |
|
1 x2 |
|
|
|
|||||||||||||||||||||||||
а также формулы, выражающие правила дифференцирования:
|
|
|
|
c u , |
c const , u u x ; |
||||||
c u |
|||||||||||
|
|
|
|
u |
|
|
|
|
u x , v v x ; |
||
u v |
|
|
v , u |
||||||||
|
|
|
|
|
|
|
|
|
|
, |
u u x , v v x ; |
u v u |
v u v |
||||||||||
|
|
|
|
|
u v u v |
|
|
|
|||
u |
|
|
|
|
u u x , v v x . |
||||||
|
|
|
|
|
|
|
|
, |
|
||
|
|
|
|
v2 |
|
|
|||||
v |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
24 |
Пример. Найти производную функции y 2x 1 ex .
Решение. По правилу дифференцирования произведения двух
функций, находим:
y 2x 1 ex 2x 1 ex 2x 1 ex .
Далее, по правилу дифференцирования суммы двух функций и произведения числа на функцию и формул производных степеней и показательной функций, находим:
|
|
|
e |
x |
2x 1 e |
x |
|
0 |
e |
x |
2x 1 e |
x |
|
y 2x |
1 |
|
|
2 x |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 1 0 ex 2x 1 ex 2ex 2x 1 ex 2x 3 ex .
Производная сложной функции
Пусть функция y f u определена на множестве D1 , а функция u g x определена на множестве D2 , причем для любой точки x D2 ,
соответствует значение u g x D1 . Тогда на множестве D2 определена функция y f g x , которая называется сложной функцией от x (или функцией от функции).
Переменную u g x |
называют промежуточным аргументом |
|||
сложной функции y . |
|
|
|
|
Пример. Функция y cos 3x является сложной функцией, так как |
||||
y cos u , u 3x . |
|
|
|
|
Пусть y f u , u g x , тогда y f g x – сложная функция с |
||||
промежуточным аргументом u |
и |
независимым аргументом |
x . |
Тогда |
производная сложной функции |
y |
по независимой переменной |
x |
равна |
произведению производной функции y по промежуточной переменной u
на производную промежуточной переменной u по независимой
|
|
|
|
переменной x , то есть yx |
fu |
ux . |
Пример. Найти производную функции y e3 x .
25
Решение. Данная функция y является сложной, так как y eu , u 3x . По правилу дифференцирования сложной функции, находим:
|
|
|
|
|
|
|
|
u 3x x e |
|
3 |
e |
|
|
3 3e |
|
. |
||||
|
yx |
yu |
ux e |
u |
u |
3 x |
3 x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Производные высших порядков |
|
|
|
||||||||||||||
Производная |
y |
|
f |
|
|
|
|
функции |
y f |
x |
|
есть также функция от |
||||||||
|
x |
|
|
|||||||||||||||||
x и называется производной первого порядка. |
|
|
|
|
|
|
|
|||||||||||||
Если |
функция |
f |
|
|
|
|
дифференцируема, |
|
то |
ее |
производная |
|||||||||
x |
|
|
||||||||||||||||||
называется |
производной второго порядка и |
обозначается |
y , то есть |
|||||||||||||||||
y y .
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается y , то есть
y y .
Производной n -го порядка (или n -й производной) называется производная от производной ( n -1)-го порядка и обозначается y n , то есть
y n y n 1 .
Пример. Найти производную третьего порядка от функции
y cos 3x.
Решение. |
|
|
|
|
|
|
|
|
|
|
sin 3x 3 3sin 3x , |
|
|
||
y cos 3x sin 3x |
3x |
|
|
||||
|
|
|
|
|
|
|
|
y y |
3sin 3x 3 |
sin 3x |
3 cos 3x 3x |
|
|||
3 cos 3x 3 9 cos 3x, |
|
|
|
|
|||
|
|
9 |
|
|
9 sin 3x |
|
|
y y |
9 cos 3x |
cos 3x |
3x |
||||
9sin 3x 3 27 sin 3x.
Итак, y y 27 sin 3x.
Дифференциал функции
26
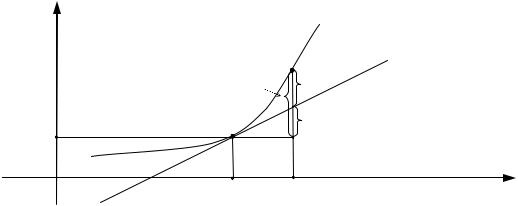
Пусть задана функция y f x и можно |
вычислить f x0 , то есть |
значение этой функции в точке x0 . Требуется |
вычислить значение этой |
функции y в точке x0 x .
Если данная функция y f x дифференцируема в точке x0 , то в точке x0 ; f x0 существует касательная l к графику функции y f x
(см. рис. 56). Тогда приращение функции y можно представить в виде:
y f x0 x x .
y |
|
|
|
y f x |
|
|
|
y |
x |
l |
|
|
|
|
|
||
f x0 |
|
|
dy |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
0 |
x0 |
|
x0 x |
|
x |
|
|
Рис. 56 |
|
|
|
Главную часть линейную относительно приращения x
независимой переменной x в последнем равенстве, то есть выражение f x0 x называют дифференциалом функции y f x в точке x0 и
обозначают dy . Итак, dy f x0 x .
При x 0, то есть при x 0 приращение функции y
приближенно равно дифференциалу dy :
y dy или f x0 x f x0 x .
Последнюю формулу применяют для приближенного вычисления значений функций в точке.
Пример. Вычислить e 0,02 . |
|
Решение. Рассмотрим функцию y ex . Пусть |
x 0 , тогда |
|
0 |
x0 x 0,02 , откуда x 0,02. |
|
27 |
|
|
|
|
|
x 0 ex |
|
x 0 e0 1, |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||
y x0 ex |
|
|
|
|
|
|
|
|
||||||||||
y x ex |
|
x 0 |
e0 1. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Следовательно, |
e 0,02 |
|
1 1 0,02 1 0,02 0,98. |
|
|
|
|
|||||||||||
Ответ: e 0,02 |
|
0,98. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Заметим, |
что |
дифференциал независимой |
переменной |
|
равен |
ее |
||||||||||||
приращению, то есть dx x |
|
|
|
|
|
|
|
|
|
|||||||||
, так как dy dx x x 1 x x . |
||||||||||||||||||
Таким образом, дифференциал функции вычисляется по формуле: |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy y x dx . |
|
|
|
|
|
|
|
|||
Пример. Найти дифференциал функции y ln cos x . |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
y |
|
|
ln cos x |
cos x cos x cos x sin x tgx , |
||||||||||||
|
|
|
||||||||||||||||
тогда dy tg dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Правило Лопиталя |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Рассмотрим способ раскрытия неопределенностей вида |
|
|
и |
|
||||||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
при вычислении пределов от функции одного переменного, который основан на применении производных.
Пусть функции |
f x |
и |
g x непрерывны и дифференцируемы в |
|||||||||||||||||
окрестности точки |
x0 |
|
и |
обращаются |
в |
нуль в |
этой точке: |
|||||||||||||
f x0 g x0 0 . Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
x0 . Тогда, если |
|||||||
g x 0 в окрестности точки |
||||||||||||||||||||
|
|
|
|
f |
|
|
|
|
f x |
|
|
|
|
|
||||||
существует предел lim |
|
x |
, |
то lim |
|
lim |
f x |
. |
|
|||||||||||
g |
x |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
g x |
|
g x |
|
||||||||||
|
|
|
x x0 |
|
|
|
|
x x0 |
|
|
|
|
|
x x0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример. Вычислить предел lim |
|
x 1 |
. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
x ln x |
|
|
|
|
|||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lim |
x 1 |
|
1 1 |
|
|
0 |
|
lim |
|
x 1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x 1 |
x ln x 1 ln 1 |
|
|
x 1 |
|
|
|
|
|
|
|
|
||||||||
|
|
0 |
|
|
x ln x |
|
|
|
|
|||||||||||
28
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0 |
|
|
|
|
|
|
|
|
|||||
lim |
|
|
x |
1 |
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
x ln x x ln x |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
x 1 |
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ln x x |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||
lim |
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
1. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
ln 1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
x 1 |
ln x 1 |
|
|
|
0 |
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Пусть функции |
|
|
f |
x |
и g x |
|
непрерывны и дифференцируемы в |
|||||||||||||||||||||||||||||||||||||||||||
окрестности точки x0 |
|
|
(кроме, |
быть |
|
может, |
самой |
точки x0 ), в |
этой |
|||||||||||||||||||||||||||||||||||||||||
окрестности lim |
f x lim g x |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
если существует |
||||||||||||||||||||||||||||||||||
|
g |
x 0. Тогда, |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x x0 |
|
|
|
|
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
f x |
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
предел lim |
|
f x |
, то lim |
|
lim |
|
|
|
|
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
g x |
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
g x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
x x0 |
|
|
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пример. Вычислить предел lim |
|
|
|
|
|
x2 1 |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
2x2 |
3x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. lim |
|
|
|
x2 |
|
1 |
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
lim |
|
x2 1 |
|
||||||||||||||||||||||||||
2x |
2 |
|
3x |
2 |
2 |
|
|
3 |
|
|
2x2 3x |
|||||||||||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x 0 |
|
|
|
|
|
|
||||||||||||||
|
|
lim |
|
|
|
|
|
1 |
|
|
lim |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
2x |
|
|
|
3x |
|
4x 3 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
x |
|
2 |
|
|
x |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
2x |
|
lim |
|
|
|
|
2 |
|
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
4x 3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
x |
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Исследование функций и построение их графиков
Одним из приложений производной является ее применение к исследованию функций и построение их графиков.
Рекомендуемая схема исследования функции:
1.Найти область определения функции. Часто полезно учесть множество значений функции.
2.Исследовать специальные свойства функции: четность, нечетность, периодичность, свойства симметрии.
3.Исследовать поведение функции при стремлении аргумента к граничным точкам области определения и к бесконечности, то есть найти асимптоты графика функции: вертикальные и наклонные. Проанализировать расположение графика функции и его асимптот.
4.Найти интервалы монотонности функции: возрастание и убывание. Найти экстремумы функции: минимумы и максимумы.
29
