
7588
.pdf
Учитывая структуру организации ВГМ, можно обобщить данный подход к смещению пространства ВГМ до многомерного случая. Сдвиг в многомерном пространстве выглядит как композиция последовательных смещений вдоль осей координат, при которых изменению подлежит одновременное изменение положения массива значений и изменение значений самой ВГМ. Характеристики ВГМ в данном случае будут определяться как:
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
' cos arcctg n ' , |
|
|
|
'2 ; n ' |
|
n ' n |
|
|
|
|
|
|
|
|
||||||
n |
' n ' |
1 n |
|
|
n |
n |
|
|
|
|
|
; n |
|||||||
in |
i |
nn |
1 |
|
n |
1 |
|
|
|
|
|
|
|
|
|
nn |
n |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
n |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||
где коэффициенты n1 |
nn – выражаются из базовых графических образов |
{ Cn1 ,Cn2 , ,Cnn } воксельной геометрической модели. |
|
При повороте |
пространства ВГМ локальные геометрические |
характеристики нормали будут рассматриваться на геометрической модели поворота вокруг заданной оси (рис. 5). Исходные данные при воксельном подходе к повороту соответствуют исходным данным при воксельном сдвиге с условием, что нормаль N 3 , вращаясь вокруг оси OZ, переходит в нормаль N 3 ' . Необходимо установить зависимость значений компонентов нормалей между собой с учётом угла поворота о.
|
|
|
|
|
|
|
x' |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
2 |
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
A' x |
B' y |
C' 0 |
3' |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
y' |
4' |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
2' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
3 |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Cn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax By C 0 |
||
|
C |
N 3 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
N |
|
3 |
' |
|
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
A |
An 0 |
|
|
An ' A' |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Bn Bn ' |
|
|
|
|
|
|
|
|
x |
||
|
|
N |
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
B B' |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
N |
2 ' |
|
|
|
1
Рис. 5. Геометрическая модель поворота прямой в двумерном пространстве
11

Для нахождения ЛГХ после поворота, необходимо воспользоваться следующими преобразованиями по аналогии матричного в декартовом пространстве:
A ' A' |
1 C '2 |
, B ' B' |
1 C '2 , C ' C' |
1 C '2 |
; |
|||||
n |
n |
|
n |
|
|
n |
n |
|
n |
|
|
|
|
|
|
cos |
sin |
0 |
|
|
|
A' |
B' C' A |
B |
C sin |
cos |
0 |
; |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
An |
|
, B |
|
Bn |
|
, C |
|
Cn |
|
, |
|
|
|
|
|
|
|
|
|
||||
|
(1 Cn2 ) |
|
|
(1 Cn2 ) |
|
(1 Cn2 ) |
||||||
|
|
|
|
|
|
|
|
|
|
где An ,Bn ,Cn выражается из ВГМ.
Поворот ВГМ в пространстве соответствует композиции поворотов вокруг осей координат. Преобразование характеристик ВГМ заключаются в нахождении новых величин компонентов нормали (параметров формы), в плоскости которых происходит вращение при сохранении параметра положения.
При повороте нормали N 3 вокруг оси OZ на угол о значения будут менять только две компоненты, соответственно An A'n , Bn B'n , при Cn const .
На рисунке 6 представлена исходная ВГМ для функции поверхности с нулевым значением в виде контура квадрата (далее по тексту «функция квадрата»). Результат поворота пространства ВГМ вокруг оси OZ тремя подходами соответствует базовым графическим образам рисунка 7.
Cx Cy Cz Ct
|
Рис. 6. Исходная ВГМ для функции квадрата |
|
|
Cx |
Cy |
Cz |
Ct |
Рис. 7. Поворот пространства ВГМ вокруг оси OZ
12

Поворот вокруг третьей оси в n -мерном пространстве на угол о представим как:
n |
' n ' |
1 n2 |
, |
n |
' n ' |
1 n2 |
, |
n ' n |
|
; |
||||||
1n |
1 |
|
|
nn |
|
2n |
|
|
2 |
|
nn |
|
in |
in |
|
|
|
|
|
|
|
|
|
|
cos |
sin |
|
0 |
|
0 |
|||
|
|
|
|
|
|
|
|
sin |
cos |
|
0 |
|
0 |
|||
1 |
n |
1 |
|
n |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
. |
|||||||||
n ' n ' |
|
n |
|
n |
|
0 |
|
0 |
|
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|||||
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При масштабировании пространства ВГМ локальные геометрические характеристики нормали будут находиться с помощью специальной геометрической модели масштабирования вдоль заданной оси (рис. 8).
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
x |
M x x |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A' x B' y C' 0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
4 |
|
Ax By C 0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
Cn ' |
|
|
|
|
|
|
1 |
|
|
|
|
3 |
N |
' |
|
|
|
|
|
3 |
|
|
|
|
|
|||
|
|
N |
|
|
|
|
Cn |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax By Cz 0 |
|
|
3' |
|
||
|
|
|
A |
|
|
An A' A ' |
|
|
|
|
|
X |
|||||||||
|
|
|
|
|
|
|
A' x B' y C' z 0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
||||||
|
N |
2 |
|
|
|
|
|
|
|
|
|
|
B |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
B |
Bnn ' |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
N 2 ' B' |
|
|
|
|
|
x |
|
|
||||||||
1
Рис. 8. Геометрическая модель масштабирования вдоль оси OX в пространстве E 2
Исходные условия для воксельного масштабирования соответствуют исходным условиям для воксельного сдвига и поворота с тем различием, что требуется установить зависимость значений компонентов нормали до и после масштабирования с учетом масштабных коэффициентов M x и M y вдоль осей ОХ и OY соответственно.
Для нахождения ЛГХ после масштабирования, можно воспользоваться следующим преобразованием по аналогии с матричным в декартовом пространстве:
13

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, С ' cos arcctg C' ; |
|||||||
|
|
A ' A' |
|
1 C |
n |
'2 , B |
' B' |
1 C |
n |
'2 |
|||||||||||||||
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
CM |
|
|
|
|
|
|
|
|
|
|
M x M yCn |
|
|
|
|||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|||||||||
A' |
B' C' A |
B C |
0 |
|
|
|
|
R |
|
|
|
0 , |
|
|
|
|
|
|
, C=ctg(arcos(Cn)). |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M 2 A2 |
M |
2 B2 |
||||
|
|
|
|
|
|
|
CM |
y |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y n |
x n |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
В отличие от рассмотренных преобразований в преобразовании
масштабирования меняются и наклон, и удаленность окрестности точки от начала координат. Таким образом, конечное значение компонентов нормали N 3 ' зависит от изменения всех трёх величин C, A и B.
На рисунке 9 представлена исходная ВГМ функции окружности, смещенной относительно начала координат на определённую величину. На рисунке 10 представлен результат масштабирования пространства ВГМ, содержащего данную функцию, вдоль оси OY.
Cx |
Cy |
Cz |
Ct |
Рис. 9. Исходная форма функции смещенной относительно центра окружности
Cx |
Cy |
Cz |
Ct |
Рис. 10. Результат масштабирования пространства ВГМ вдоль оси OY , содержащего функцию смещенной окружности
14

Ниже представлено обобщение преобразования пространства на
многомерный случай для масштабирования:
|
|
|
|
|
|
|
|
R |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
n M |
|
|
|
|
|
|
n |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M k nnn |
|
|
|||||
|
|
|
|
|
|
|
n0 |
1 |
|
|
|
|
|
|
|
|
|
|
||||||||
nin ' ni ' |
1 nnn ' |
2 |
, |
n1 ' |
nn ' n1 |
|
|
|
R |
|
|
, R |
|
; |
||||||||||||
|
nn |
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
n |
M |
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
n |
M |
|
|
|
k |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
n 1 |
|
|
|
|
|
|
|
|
|
n |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M m |
ni |
||||||||
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
i 1 |
k 1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nn ctg arccoc nnn ; |
nnn ' cos arcctg nn ' . |
|
|
|
|
|
|
|
|||||||||||||
n1 nn и nnn выражаются из ВГМ.
Вчетвёртой главе проиллюстрирован принцип R-функционального моделирования пространства геометрических объектов сложной формы. Реализованы теоретико-множественные операции над пространствами ВГМ на основе R-функционального моделирования. Отражена тройственность вычислительного подхода к множественным операциям над пространствами ВГМ. В качестве примера моделирования пространства ВГМ выполнена комплексная компоновка функций на основе предложенных геометрических преобразований, а так же произведено сравнение времени выполнения операций компоновки пространства ВГМ, содержащего функции различной сложности. Приведено экспериментальное применение результатов диссертационной работы.
Основные теоретико-множественные операции, такие как объединение и пересечение, реализуются с помощью R-функционального моделирования. Особенностью предикатного принципа построения R-функциональной конструкции является применение пространства увеличенной размерности. Данная особенность удачно коррелируется с функционально-воксельным представлением модели.
Втеории Рвачёва полная α-система R-функций, применяемая в аналитическом моделировании представлена системой уравнений:
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W1 |
|
2 |
2 |
2 W1W2 ; |
- объединение функций; |
|
|||||
R |
|
|
|
|
W2 |
W1 |
W2 |
|
|||||||
|
|
|
|
||||||||||||
|
|
1 |
W W |
|
|
|
|
; |
- пересечение функций; |
(1) |
|||||
|
|
|
|
1 |
|
|
|
|
|||||||
R |
W 2 |
W 2 |
2 W W |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
2 |
1 |
2 |
|
|
- операция инверсии над функцией, |
|
|
|
W . |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
W1 |
|
|
|
|
|
|
|
|
|
|
|||||
где 1;1 - функция, влияющая на форму поверхности функции, применяемая при решении краевых задач.
ВГМ позволяет применять операции R-функций для конструирования сложной ВГМ как результата синтеза из нескольких ВГМ.
15

Функциональный подход теоретико-множественных операций для метода ФВМ характерен использованием значения аналитического выражения функции как одного из предикатов в выражении (1), для создания ВГМ как результата синтеза нескольких функции, описанных в едином пространстве.
Функционально-воксельный подход использует ранее созданные ВГМ для последующего моделирования. Выражение линейной аппроксимации xi F( n1 ,n2 ,...,ni 1 ,x1 ,x2 ,...,xi 1 ) формирует поле значений для каждой из функцийпредикатов, достаточное для R-функциональной процедуры и последующего
построения сложной ВГМ. Для двух функций вида f ( x1 ,x2 ) |
функционально- |
|||
воксельный подход представим как: |
|
|
|
|
x31 F( n11 ,n21 ,n31 ,n41 ,x11 ,x21 ) , |
x32 F( n12 ,n22 ,n32 ,n41 ,x12 ,x22 ) , |
|
||
|
|
|
|
|
x3 x31 x32 ( x31 |
)2 ( x32 )2 , при α=0. |
(2) |
||
Коэффициенты n1 ,n2 ,n3 ,n4 вычисляются для каждой точки предиката исходя из числового значения пикселя ВГМ. Результатом является ВГМ: Cx1 ,Cx 2 ,Cx3 ,Cx 4 как результат объединения двух ВГМ: ВГМ1: Cx11 ,Cx12 ,Cx13 ,Cx14 , ВГМ1: Cx21 ,Cx22 ,Cx23 ,Cx24 .
Реализация воксельного подхода к моделированию множественных операций на тех же принципах, что и арифметические операции с применением ВГМ или геометрические преобразования пространства ВГМ не представляется возможной, поскольку аргументами операции выступают непосредственно значения самих функций. Однако к воксельному подходу решения можно прийти через имеющиеся в арсенале метода воксельные арифметические операции. Для этого уравнения (2) необходимо разложить на составляющие: определить
воксельное сложение x31 x32 , отдельно сложить воксельные |
умножения x31 x31 |
и |
x32 x32 , а затем воксельно извлечь корень и т.д. Однако |
в методе ФВМ |
на |
современном этапе не разработано воксельных операций решения подкорневых выражений. Вместе с тем, в теории Рвачёва значение 1 в выражении (1) приводит систему к упрощённому виду:
x3 12 x31 x32 x31 x32 .
Тогда воксельный подход с применением имеющихся в арсенале метода математических конструкций при теоретико-множественных операциях сводится к определению новых коэффициентов уравнения касательной в точке через последовательность отдельно выполненных арифметических операций.
В качестве примера R-функционального моделирования пространств ВГМ на рисунке 12 проиллюстрирован результат сложения и пересечения функций окружностей, представленных на рисунке 11.
16
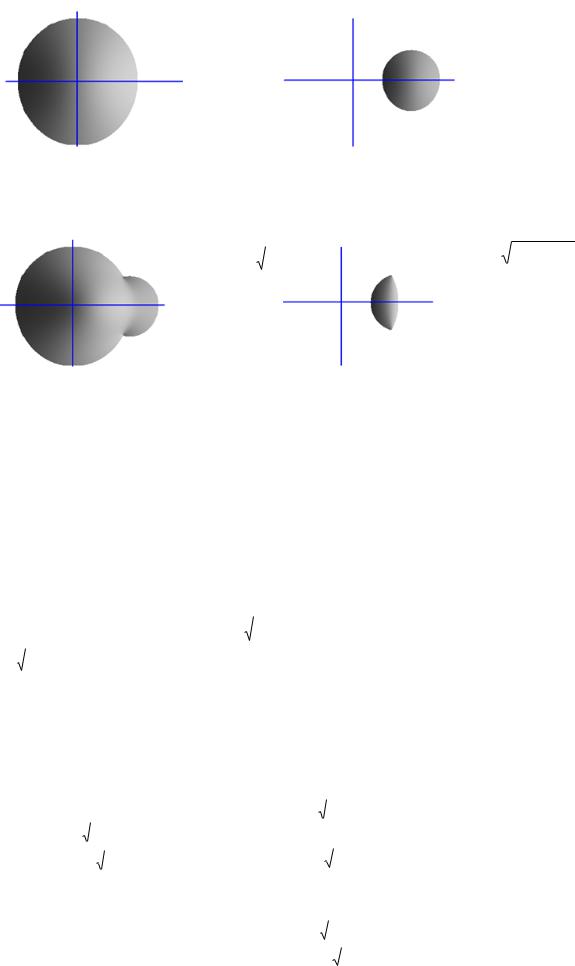
W x2 |
y 2 |
1; |
W (x 1)2 |
( y2 ) 0.52 |
1 |
|
|
2 |
|
а) ВГМ1 |
б) ВГМ2 |
Рис. 11. Задание ВГМ двух окружностей, подлежащих теоретико-множественным преобразованиям
|
|
|
Wобщ W1 W2 |
2 |
2 |
|
|
|
|||
Wобщ W1 W2 |
2 |
2 |
W1 |
W2 |
|
W1 |
W2 |
|
|
|
а) б)
Рис. 12 Сложение и пересечение окружностей W1 и W2 а) W1 W2 б) W1 W2
В работе был выполнен анализ по времени выполнения алгоритмов компьютерного расчёта для процедур: сдвига, поворота и масштабирования
предложенными подходами: функциональным (F), функционально-воксельным
(FV) и воксельным (V). Для FV и V подходов в качестве исходных данных были использованы образы, полученные функциональным способом (Fисх). Для сравнения было выбрано шесть функций различной сложности.
Три функции аналитического описания:
1. f |
100 x 20 2 |
y 20 2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 15 2 y 10 2 6 x 15 2 |
||||||||
f |
|
|
cos(0.4x) cos(0.4 y) |
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y tg 0.1x |
|
|
|
|
|
||||||||||
|
|
|
|
cos(0.4x) cos(0.4 y) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2. |
f |
|
|
|
; |
36 x 15 2 y 10 ; |
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
y tg 0.1x |
|
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
Три функции кусочно-аналитического вида, описанные с помощью |
||||||||||||||||||||||||
аппарата R-функционального моделирования: |
|
|
|
|
|
|
|
|
||||||||||||||||||
4. W1 y 2 1.8x; |
|
|
|
5. |
W1 3 x; |
|
|
|
|
|
|
|
|
|||||||||||||
|
W2 y 2 1.8x; |
|
|
|
|
|
W2 3 x; |
|
|
|
|
|
|
|
|
|||||||||||
|
W3 y 1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
W1 2 W1 W2 W12 W22 ; |
||||||||||||||||||||
|
|
|
|
|
|
|
W3 y 14; |
|
|
|
|
|
|
|
|
|||||||||||
|
W1 2 W1 W2 W12 W22 ; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
W1 2 3 W1 2 W3 W1 |
22 |
W32 ; |
|||||||||||||
|
Wтр еуг W1 2 W3 |
W1 |
22 W32 . |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
W4 y 2x 18; |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
W5 y 2x 18; |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
W4 5 W4 W5 W42 W52 ; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
Wtelo |
W1 2 3 W4 5 W1 |
22 3 W425 . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Шестая функция представляет результат R-функционального объединения одиннадцати функций по аналогии с функциями 4 и 5.
Время работы алгоритмов представлено в таблице 1.
Анализ результатов показал, что наибольшую эффективность по времени расчёта разработанные подходы к преобразованию пространства в ФВМ показывают при работе со сложными функциями. Это позволяет повышать эффективность пространственных преобразований, многократно ускоряя их расчёт с применением метода функционально-воксельного моделирования.
Таблица 1 Время работы алгоритмов компьютерного расчёта для процедур преобразования пространства
в ФВМ в секундах
№ |
|
Смещение |
|
|
Поворот |
|
Масштабирование |
|||||
функции |
|
|
|
|
|
|
|
|
|
|
|
|
Fисх |
F |
FV |
|
V |
F |
|
FV |
V |
F |
FV |
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0,58 |
0,59 |
1,04 |
|
0,91 |
0,77 |
|
1,4 |
1,25 |
0,73 |
2,05 |
2,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0,78 |
0,78 |
0,89 |
|
0,87 |
1,18 |
|
1,36 |
1,26 |
1,13 |
2,28 |
2,33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1,04 |
1,14 |
0,89 |
|
0,87 |
2,36 |
|
1,38 |
1,27 |
1,63 |
2,31 |
2,46 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1,44 |
1,46 |
0,87 |
|
0,87 |
3,35 |
|
1,28 |
1,24 |
2,39 |
2,02 |
2,14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
2,7 |
2,71 |
0,86 |
|
0,86 |
8 |
|
1,32 |
1,22 |
4,95 |
2,04 |
2,15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
91,95 |
99,76 |
0,87 |
|
0,86 |
298,46 |
|
1,28 |
1,22 |
180,16 |
2,05 |
2,16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Разработанные подходы в функционально-воксельном моделировании были применены в работах, связанных с технологиями прототипирования. Воксельное представление компьютерных геометрических моделей изделий в аддитивном производстве открывает новые возможности в управлении и контроле модели в части создания сложнопрофильных тонкостенных структур с внутренними полостями. ВГМ представляет дополнительные возможности в автоматизированных инженерных расчетах и топографической оптимизации. Результаты настоящей работы апробированы для создания геометрических моделей образцов сложной геометрической формы, изготовленных методом селективного лазерного плавления порошков функциональных композитных материалов. Так же разработанные алгоритмы преобразования пространства функционально-воксельной модели были применены в качестве программного модуля для создания геометрических объектов, необходимых для 3D печати методом послойной засветки жидкого полимера в установке быстрого прототипирования.
Основные результаты и выводы
1. Разработаны алгоритмы преобразования пространства аналитической модели, представленной ВГМ на основе локальных геометрических
18
характеристик. Такие алгоритмы рассчитывают преобразование простыми алгебраическими зависимостями между характеристиками ВГМ в обход зачастую сложному пересчёту самого аналитического объекта.
2.Приведены к матричному представлению геометрические преобразования пространства функционально-воксельной модели, представленной локальными геометрическими характеристиками, что позволяет строить любые сложные преобразования на основе традиционных подходов в компьютерной графике.
3.Разработан тройственный вычислительный подход к построению алгоритмов преобразования пространства ФВМ, позволяющий расширить инструментальные средства обработки модели, повышая эффективность расчётов для различных условий задания модели.
4.Применение описания функции нормальным полем в пространстве увеличенной размерности позволяет иметь достаточную информацию для построения геометрических преобразований, что позволяет эффективно использовать такую модель в расчётах и строить различные математические конструкции, включая R-функциональное моделирование для построения сложных геометрических объектов.
5.Разработанные функционально-воксельный и воксельный подходы к геометрическим преобразованиям ВГМ по аналогии с традиционным функциональным подходом применимы к работе с многомерным воксельным пространством, что обеспечивает возможность использования воксельных моделей в построении многомерных задач геометрического моделирования.
Публикации по теме диссертационной работы
Статьи, опубликованные в изданиях, рекомендованных ВАК:
1.Лоторевич, Е.А. Автоматизация графического способа решения некоторых математических задач/ С.Н. Григорьев, Е.А. Лоторевич, С.А. Пушкарев, Д.А. Силантьев, А.В. Толок // Прикладная информатика. – 2012. – № 5 (41). – С. 44-50.
2.Лоторевич, Е.А. Принципы пространственной визуальной компоновки аналитических моделей, отображённых в воксельном графическом пространстве/ Е.А. Лоторевич // Технология машиностроения. – 2013. – № 11. – С. 59-63.
3.Лоторевич, Е.А. Визуализация математического моделирования при определении рабочих поверхностей деталей / С.Н. Григорьев, Е.А. Лоторевич, С.А. Пушкарев, Д.А. Силантьев, А.В. Толок // Технология машиностроения. –
2013. – № 2. – С. 57-60.
19
4.Лоторевич, Е.А. Воксельно-математическое моделирование при решении задач определения площади для поверхностей деталей / Е.А. Лоторевич, С.А. Пушкарев, Д.А. Силантьев, А.В. Толок // Информационные технологии в проектировании и производстве. – 2013. – № 3 (151). – С. 29-33.
5.Лоторевич, Е.А. Определение метода прототипирования для разработки офисного 3D принтера / Е.А. Лоторевич, С.А. Пушкарев, Д.А. Силантьев, А.В. Толок, А.Н. Феофанов // Технология машиностроения. – 2014. – № 2. – С. 58-63.
Статьи в сборниках научных трудов и сборниках конференций:
6.Лоторевич, Е.А. Применение воксельных геометрических моделей для решения задач компоновки функции / Е.А. Лоторевич, А.В. Толок // Системы проектирования, технологической подготовки производства и управления этапами жизненного цикла промышленного продукта CAD/CAM/PDM-2015: тр. 15-ой междунар. конф. – М.: ООО Аналитик, 2015. – С. 47-51.
7.Лоторевич, Е.А. Разработка геометрических принципов воксельного моделирования / Е.А. Лоторевич, А.В. Толок // XII всероссийское совещание по проблемам управления ВСПУ-2014: сб. докл. – М., 2014. – С. 9301-9308.
8.Лоторевич, Е.А. Воксельное графическое 3D-моделирование / Е.А. Лоторевич, А.В. Толок // Системы проектирования, технологической подготовки производства и управления этапами жизненного цикла промышленного продукта CAD/CAM/PDM-2013: тр. 13-ой междунар. конф. – М.: ООО Аналитик, 2013. – С.
205-209.
9.Лоторевич, Е.А. Растровое представление геометрической модели / С.Н. Григорьев, Е.А. Лоторевич, С.А. Пушкарев, Д.А. Силантьев, А.В. Толок // Системы проектирования, технологической подготовки производства и управления этапами жизненного цикла промышленного продукта CAD/CAM/PDM-2012: тр. 12-ой междунар. конф. – М.: ООО Аналитик, 2012. – С. 47-50.
10.Лоторевич Е.А. Тройственность подхода к задачам преобразования пространства функционально-воксельной модели / Е.А. Лоторевич, А.В. Толок // GraphiCon2016: тр. 26-й Междунар. конф. по компьютерной графике и зрению. – Нижний Новгород, 2016. – С. 81-84.
20
