Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

7582

.pdf

Скачиваний:

Добавлен:

23.11.2023

Размер:

1.16 Mб

Скачать

☆

<<< < Предыдущая 12 / 22

	d	k ctg ds ctg d = 0 .	(12)

	cos sin

Поскольку k∙ds=dδ, где dδ – приращение угла наклона δ орта			от его

первоначального положения, то приняв dδ=dβ/m, после интегрирвания получим:

ln \| tg \|	ln \| sin \|	ln \| sin \| C ,	(13)
	m

где m – скалярный параметр. В итоге получим решение для угла α:

m 1

= arctg eC

sin

(14)

где n∙π ≤ α < (2n+1)∙π/2, β = m∙δ.

Определяя

угол

k ds

для заданой плоской кривой

учитывая предыдущие формулы,

получим

развертывающуюся

линейчатую

поверхность.

зависимости от формы плоских

кривых

параметра

определяющего

положение

Рис. 6.

Семейство торсовых поверхностей

образующей

прямой,

можно

для окружности при m=0,2; m=1

получать

различные

виды

соответственно

торсовых поверхностей (рис. 6).

При этом вместо соотношения β=m∙δ можно принять любой закон изменения угла β. Предложенный дифференциально-геометрический подход позволяет в режиме прямого счета на основе изменения геометрических параметров модели получать интерактивно различные виды развертывающихся линейчатых поверхностей.

Втретьей главе рассмотрены теоретические вопросы соприкосновения линейчатых поверхностей.

Впараграфе 3.1 приведены сведения по соприкосновению косых линейчатых поверхностей, исследованного К.Л. Панчуком. Основные из них:

- уравнение линейчатой поверхности в дуальной векторной форме имеет

вид:

t a

t , ω2=0,

где

- единичный вектор образующей

прямой,

11 t

- момент вектора

относительно начала координат системы

отнесения, А1(t) - дуальный единичный вектор с координатным представлением

y2 z2

1 , t – вещественный параметр T

ix jy kz , при этом x 2

≤ t ≤ T

;

- существует триэдр линейчатой поверхности с дуальными ортами

А1 ;

~ * ;

A1 t0 A1 t0

~ / ~ //

A t A* t ; A t A* t ;

1 0 1 0 1 0 1 0

~ ///

A (t ) A * t .

1 0 1 0

;

А А

и деривационными уравнениями

H А2 ;

H А1 Q A3 ;

Q A2 ;

А1

А2

• дуальный вектор расхождения двух линейчатых поверхностей с общей образующей имеет выражение:

			~						~	/
G t A	t	0	- A* t	0	A		t	0	A *		t	0
1		0	1	0		1		0		1		0

A t

- A *

... ;

(15)

- порядок соприкосновения линейчатых поверхностей определяется:

lim

g t

0 , где g(t) - модуль дуального вектора расхождения;

Δt→0

Δt

- соприкосновения начальных порядков характеризуются:

n=0 (пересечение по общей образующей) - A1 t 0 A1* t 0 ; A1 t 0

A1* t 0

;

n=1 -

A1 t 0 . При n=1 в центральной

A1 t 0 A1 t 0 ; A1 t 0

A1 t 0 ; A1 t 0

точке общей образующей соприкасающиеся линейчатые поверхности имеют совпавшие триэдры и равные элементы дуальных дуг, их стрикции пересекаются в центральной точке так, что касательные к стрикциям в этой точке инцидентны касательной плоскости соприкасающихся линейчатых

поверхностей; n=2 -

	В	общей образующей выполняются равенства	~ ~	~ ~
			H H t ; H (H t )t ;
~	~	раскрытие которых приводит к следующим результатам:		стрикции
Q Q t ,

соприкасающихся линейчатых поверхностей имеют в центральной точке образующей соприкосновения общую касательную, инцидентную касательной плоскости этих линейчатых поверхностей; совмещены триэдры эволют первого

порядка	соприкасающихся		линейчатых	поверхностей; равны		их дуальные
радиусы	кривизны	~		R=R(s) -	дуальный	угол между
		sinR , где
соответствующими образующими ЛП и ее линейчатой эволюты.
В	параграфе	3.2	выполнено	решение	задачи по	построению

соприкасающихся развертывающихся поверхностей (торсов), основанное на результатах п.п. 3.1. В отечественной и зарубежной научной литературе эта задача, несмотря на ее практическую востребованность, находится в начальной стадии рассмотрения. Для двух торсов условие n=0 означает пересечение по общей образующей. Рассмотрим соприкосновение n=1. Для двух торсов А1(t) и

~ ~	~
А1( t ) параметры Р и	P их образующих равны нулю и поэтому элементы их
дуальных дуг ∆s и	~	~	. Поэтому триэдры
дуальных дуг ∆s и	s -	вещественные числа ∆s0 и s0	. Поэтому триэдры
линейчатых поверхностей		в центральной точке A их	общей образующей
		12

ds(1)

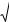
совпадают		с	трехгранниками			стрикций -		ребер	возврата	торсов:
а01, а02, а03		~	~	~	Исходя	из	условий	соприкосновения		n=1,
		а01, а02		, а03 .
приведенных в п.п. 3.1, и учитывая, что дуальное равенство									~
									ds ds для торсов
становится		вещественным			~	, то	поскольку ds0 k dσ получаем, что
					ds0 ds0
~	~	Следовательно, произведение кривизны на элемент дуги стрикции
k dσ k	dσ .

для обеих стрикций в их точке касания равны. Для торсов соприкосновение n=2 исследуется на результатах этого соприкосновения для косых линейчатых поверхностей, приведенных в п.п.3.1. На основании этих результатов, с учетом выражений для вторых производных

~ ~

~ 2

~ ~

~ 2

-H

H Q A

(16)

A H

, A

H t

H Q t

~ ~

следуют дуальные уравнения H H t ; H (H t )t ; Q Q t , раскрытие которых, с

учетом уравнений стрикций соприкасающихся торсов, приводит к выражениям

~	~
dσ dσ ,	k k , что означает равенство элементов дуг и кривизн стрикций торсов
в центральных точках		~
в центральных точках		A A их совмещенных образующих прямых линий
~	. На основании этого результата и, учитывая, что для элемента ds(1)
а01 а01

дуальной дуги, образованной перемещением бинормали а03 , можно записать

дуальные равенства ds(1) ds01 ωds11 Q dt (q0 ωq1)dt ,					из которых, по
разделении главных и моментных компонент
	~ ~	~	~	~
	ds01 q0dt q0 t dt q0d t ds01,
	~	~	~	~	(17)
	ds11 q1dt dσ dσ	q1dt		ds11	(17)
следует результат	~
следует результат	ds(1) ds(1) , означающий равенство элементов дуальных дуг

бинормалей стрикций соприкасающихся торсов. На основании известной в линейчатой геометрии формулы d e / , с учетом последнего

результата, получаем ~ , что означает равенство кручений рассматриваемых

стрикций. Последовательное выполнение исследований, подробно изложенных в настоящем параграфе работы, привело к получению следующих результатов по соприкосновению n=2: выполняется равенство параметров дуальных дуг

бинормалей

стрикций

равны

элементы

дуальных дуг

P(1) P(1) ;

ds ds ,

описываемых нормалями

а02

стрикций

равны

параметры

à02

этих

элементов;

равны

дуальные

кривизны

/(k 2

2 ) P

/(k2 2 )

соприкасающихся

торсов

и равны дуальные углы

R R0 R1 ,

определяющие

положение

единичных

R 0 R1 ,

R R ,

дуальных векторов главных нормалей

и B1 торсов;

совмещены триэдры

эволют

первого

порядка

B1 B1, B2 B2 , A2 A2 ;

равны

дуальные

изгибы

соприкасающихся

d s

торсов в их общей образующей; совмещены

триэдры

эволют

второго

порядка

B1 B1, C1 C1

, C2 C2

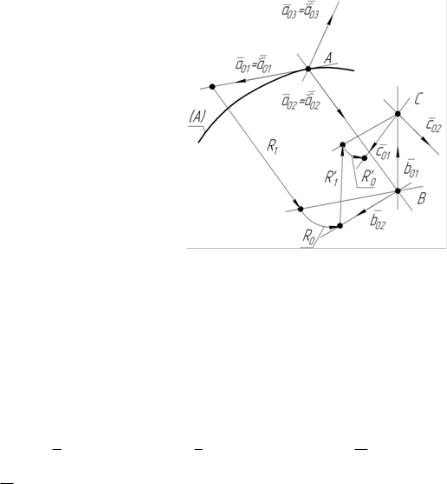
этих торсов (рис.7). На

основании проведенных исследований сделан

общий вывод о том, что для полного

соприкосновения n=2 торсовых поверхностей

необходимо, чтобы

в их общей образующей

Рис. 7. К соприкосновению двух

выполнялось

равенство

значений

дуальных

торсовых поверхностей

изгибов

параграфе

3.3

рассмотрены примеры

применений теоретических

результатов п.п. 3.1, 3.2 в задачах конструирования линейчатых полос из сегментов торсовых поверхностей, построенных на основе эрмитова сплайна пятой степени, выражение для которого получается из общего уравнения эрмитова сплайна нечетной степени:

t = 1 10t3

15t 4

5 P

10t3

15t 4

6t5 P

t 6t3

8t 4

5 P

4t3 7t 4 3t

5 P

i 1

t 2

t 4

(18)

i 1

Последнее уравнение может быть представлено в матричном виде [Fi ]= [T][Gi], где [Т] - матрица весовых коэффициентов, [Gi] - матрица геометрии соответственно:


[T] [1 10t 3 15t 4 6t 5 ,10t 3									15t 4						6t 5 , t 6t 3 3t 5 8t 4 ,7t 4 4t 3 3t 5 ,
	1	t	2		3	t	3		3		t	4		1		t	5	,	1	t	3		t	4	1	t	5	];
2		t			2	t		2			t			2		t		,	2	t			t		2	t		];
2					2			2						2					2						2			(19)
								,					,								,				]T
			[G	i	] [P			,		P			,		P , P						,	P ,		P	]T
				i				i i 1							i			i 1					i	i 1

[Pi] – матрица-столбец координат граничных условий (точек либо касательных). Уравнение торсовой поверхности в этом случае может быть

записано в следующем обобщенном виде:		(t, u)		(t) u
	F		F		F (t); t [0,1] . Первый
	i		i		i

порядок гладкости стыковки торсов для рассматриваемого случая может быть получен при сонаправленности векторов главных нормалей в узлах сегментов кусочного сплайна, различающихся дополнительными множителями (рис.8). Матрицы геометрий для трех сегментов в рассматриваемом случае имеют вид:

							T																	T
															T										. (20)
								, [G							T	, [G		] [P , P
[G ] [P , P , P , P					, P, P ]			, [G	2	] [P , P , P			, P , a P , P ]			, [G	3	] [P , P		, P , P , b P , P ]
1	1	2	1	2	1	2			2	2	3	2	3	2	3		3	3	4	3	4	3	4

Эрмитовы сплайны пятой степени с непрерывной производной третьего и четвертого порядков в узлах сегментов получаются на основе решений системы уравнений:


		IVi (t 1)				IVi 1(t 0) 0,
F				F				(21)
			'''i (t 1)			'''i 1 t 0	0.
	F				F

Раскрывая и группируя члены последних уравнений, получим систему:

3 P

60 P

120 P

3 P 18

60 P 24 P ,

i 2

i 1

(22)

168

384

168

360

360 P 24 P.

i 2

Из системы (22) определяются первые и вторые производные в узлах интерполяции [P′′i+1], [P′i+1], где i =[1, n-1] в

точке соединения соседних сегментов. Параметрические уравнения сегментов образующихся кусочных Эрмитовых сплайнов определяются: [F1] = [T]∙[G1]; [F2] = [T]∙[G2]; [F3] = [T]∙[G3].

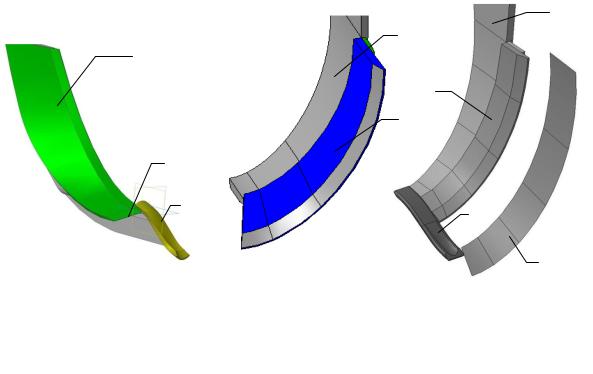
Кусочные сплайны с непрерывными производными второго и третьего порядков в узлах дают неполный второй порядок гладкости стыковки торсов.

Кусочному сплайну с непрерывной четвертой производной в узлах соответствуют торсы, состыкованные по второму порядку гладкости (совпадают трехгранники стрикций; равны кривизна и кручение в узлах стыка, равны

Рис. 8. Линейчатая полоса первого порядка гладкости стыковки сегментов

дуальные изгибы ). Если добавить циклические условия на концах, например, сплайна (20), то получим замкнутый кусочный сплайн и соответствующую полосу (рис. 9). При сферическом отображении этого сплайна можно получить линейчатые полосы второго порядка гладкости из сегментов сферических торсов.

Вчетвертой главе выполнено

приложение	полученных	теоретических	Рис. 9. Замкнутая линейчатая

результатов к решению прикладной задачи по			полоса неполного второго
конструированию лемешных		поверхностей	порядка гладкости сегментов

рыхлителя почвы.

В параграфе 4.1 на основе анализа существующих исследований по конструированию рыхлителей сделан вывод о необходимости геометрического

моделирования рабочей поверхности лемеха рыхлителя, закрепляемого на различных видах стоек.

В параграфе 4.2 рассмотрено решение задачи конструирования лемешной поверхности для прямой и цилиндрической стоек. Конструирование лемешной поверхности стойки состоит в получении линейчатой поверхности, дающей необходимую информацию и возможность изменения угла крошения

лемеха (рис. 10). Представим ее
в	виде			линейчатой
развертывающейся					полосы,
имеющей		вогнутую		форму и
выполненную			эквидистантно
лобовому		профилю			стойки
рыхлителя. Такой лемех имеет
вогнутый профиль, соответст-
вующий		минимальной			энерго-
емкости		захвата и		отведения
пласта,			осуществляет			Рис. 10. а) соприкосновение пары линейчатых

минимальный оборот агрегатов сегментов; б) линейчатая полоса, представляющая
почвы		в	пласте,		что	лемешную поверхность при m= -0.43 и αmax = 260

способствует ровной пахоте и дополнительному крошению почвы. Все это приближает процесс рыхления к условиям минимальной обработки почвы.

Поперечный профиль таких стоек определяется по формуле логарифмической спирали:

g = r e t cost		r e t sin t
g = r e t cost	i	r e t sin t	j 0 k ,				(23)

при этом r – эмпирический параметр, зависящий от ширины долота и глубины рыхления. Дуга логарифмической спирали рассчитывается, исходя из глубины рыхления до 650 мм, при этом рекомендуется выбрать r = 7. Граничные точки профиля стойки определяются из условия g k 1, g k 0 , из которого следует

t1=-π/4+n∙π; tk=π/4+n∙π.

На практике применяются конструкции рыхлителей с прямыми стойками с приемлемой геометрической формой в виде полупараболического

продольного профиля с началом в нижней точке: g = at2 i 2 at j , где а – параметр, отвечающий за кривизну параболы, который может быть подобран из условия минимизации тягового сопротивления при равенстве движущих сил и сил сопротивления при установившемся движении рыхлителя, например, а = 40. Полученный продольный профиль в виде логарифмической спирали удобнее аппроксимировать дугами окружности. Из получившихся линейчатых сегментах затем строится линейчатая развертывающаяся полоса.

Аппроксимация дугами окружностей выполняется радиусо-графическим способом. В результате на основании формул п.п. 2.3 получаем линейчатые сегменты

		[L]=[o]+[l]∙T,					(24)
		( cos n sin ) cos		sin ; arctg(		m 1

где	l		b		sin(mt)	m ) ;	[o] – коорди-

натно-параметрические уравнения дуги окружности; T – параметр положения точки на образующей, m – скалярный параметр, t – параметр точки на кривой, представляющей профиль стойки. Скалярный управляющий параметр m,

логарифмической спирали, t=[0; 1.4937] рад.

Приводя сегменты в соприкосновение по первому порядку гладкости, получаем линейчатую полосу. Триангулированные уравнения полученной линейчатой полосы распечатывается в структурированный текстовый файл «CSV» или в форматированный файл «TXT». После чего данные о линейчатой полосе могут быть импортированы в практически любую САПР.

В работе выполнено построение твердотельной модели рыхлителя в системе Компас 3D. Импорт поверхности лемеха стойки в Компас 3D выполняется при помощи выстроенной команды «Поверхность по сети точек» (рис. 12). Благодаря наличию SDK и параметрическому моделированию в системе Компас 3D выполнена параметрическая модель изделия. Такая модель требует специфических сведений о типах применяемых почв и вариантах конструкций рыхлителей. Предложенная математическая модель лемешной

поверхности рыхлителя и ее конструкция приняты к внедрению на ФГУП «Омский экспериментальный завод».

				1
	2
					2
				2

		1


			3			3
						3


							Лемешная
							поверхность

а)				б)
	Рис. 12. Параметрическая модель рабочих органов рыхлителей со
	стойкой 1, долотом 3 и лемехом 2, выполненная в САПР Компас 3D
	а) с параболической стойкой; б) с криволинейной стойкой

Основные результаты и выводы

1.Разработан новый метод конструктивно-метрического образования линейчатых поверхностей. Отличительной особенностью метода является возможность получения алгебраических линейчатых поверхностей и плоских алгебраических кривых высоких порядков при пониженных, в сравнении с известными методами, порядках проективных рядов, пучков прямых и плоскостей.

2.Разработан новый метод дифференциально-геометрического образования развертывающихся поверхностей на основе дифференциальной геометрии плоской кривой, позволяющий выполнять математическое описание линейчатых поверхностей в векторно-параметрической форме. Отличительной особенностью метода является возможность получения в режиме прямого счета, на основе изменения геометрических параметров, различные виды торсовых поверхностей.

3.Разработан математический инструментарий стыковки развертывающихся поверхностей, позволяющий образовывать полосы из линейчатых сегментов, состыкованных по определенным порядкам гладкости. Вопросы сегментарного конструирования линейчатых полос по различным порядкам гладкости рассматриваются впервые.

4.Выполнено практическое применение полученных теоретических результатов исследований в задаче параметрического конструирования лемешных поверхностей рыхлителей почвы с возможностью управления

формой рабочей поверхности исходя из технологических условий почвообработки.

Публикации по теме диссертационной работы

Статьи, опубликованные в изданиях, рекомендованных ВАК:

1.Нитейский, А. С. Конструирование торсовой поверхности методом подвижного трехгранника Френе / А. С. Нитейский // Омский научный вестник.

–2013. – № 2 (120). – С. 151-153.

2.Нитейский, А. С. Элементы теории соприкосновения линейчатых развертывающихся поверхностей / А. С. Нитейский, К. Л. Панчук // Вестник кузбасского государственного технического университета. - 2012. - Вып. 6 (94).

–С. 112-117.

3.Нитейский, А. С. Соприкосновение линейчатых развертывающихся поверхностей [Электронный ресурс] / А. С. Нитейский, К. Л. Панчук // Инженерный вестник дона. - 2012. - № 3. – Режим доступа: http://ivdon.ru/magazine/archive/n3y2012/930/

4.Панчук, К. Л. Элементы теории соприкасающихся линейчатых поверхностей/ К. Л. Панчук, А.С. Нитейский// Вестник Сибирской государственной автомобильно–дорожной академии (СибАДИ). – 2012. – Вып.

4(26).–С. 84–90.

5.Нитейский, А. С. Конструирование линейчатой поверхности на основе проективных пучков прямых / А. С. Нитейский, К. Л. Панчук // Омский научный вестник. – 2011. – № 3(103). – С. 13 – 17.

Статьи в сборниках научных трудов и сборниках конференций:

6.Нитейский, А. С. О конструировании линейчатых развертывающихся полос / А. С. Нитейский // Информационно-телекоммуникационные системы и технологии (ИТСиТ-2012): матер. Всерос. молодежной конф. – Кемерово, 2012.

–С. 232– 233.

7.Нитейский, А.С. Конструктивно аналитическое описание образования квазиподэр [Электронный ресурс] / А.С. Нитейский, К. Л. Панчук // Прикладная геометрия. - 2011. – Вып. 13. - № 27. – С. 12-21. – Режим доступа: http://www.apg.mai.ru/Volume13/Number27/nit1327.pdf

8.Нитейский, А.С. Конструктивно-метрическое образование квазиподэр/ А. С. Нитейский, К. Л. Панчук // Ориентированные фундаментальные и прикладные исследования – основа модернизации и инновационного развития архитектурно-строительного и дорожнотранспортного комплексов России: матер. Всерос. 65-й науч. - техн. конф. ФГБОУ ВПО «СибАДИ» (с междунар. участием). – Омск, 2011. – Кн. 2. – С.

270– 275.

9.Нитейский, А. С. Конструктивно-метрический подход к образованию плоских алгебраических кривых/ А. С. Нитейский, К. Л. Панчук // Современное состояние, развитие инженерной геометрии и компьютерной графики в условиях информационных и компьютерных технологий: тр. междунар. науч.- метод. конф. – АЛМАТЫ. - 2011. – С. 62-70.

Свидетельства о регистрации программ для ЭВМ:

10.Нитейский, А.С. Программа моделирования лемешной поверхности рыхлителя на основе линейчатой развертывающейся полосы / А. С. Нитейский: М.: ИНиПИ РАО, 2013. - № 50201350848. Свидетельство о регистрации электронного ресурса № 19375 от 22.07.2013.

11.Нитейский, А. С. Программа «Компьютерного моделирования

алгебраических линейчатых поверхностей высших порядков на основе проективного метода» / А. С. Нитейский, К. Л. Панчук: М.: ИНиПИ РАО, 2013. - № 50201350152. Свидетельство о регистрации электронного ресурса № 18925 от 12.02.2013.

12. Нитейский, А. С.		Программа	«Компьютерного моделирования
плоских	алгебраических	кривых	высших	порядков	на основе

проективного метода» / А. С. Нитейский, К. Л. Панчук: М.: ИНИПИ РАО, 2013. - № 50201350153. Свидетельство о регистрации электронного ресурса № 18924 от 12.02.2013.

<<< < Предыдущая 12 / 22

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.11.20231.16 Mб07578.pdf
#
23.11.20231.16 Mб07579.pdf
#
21.11.2023149.02 Кб0758.pdf
#
23.11.20231.16 Mб07580.pdf
#
23.11.20231.16 Mб07581.pdf
#
23.11.20231.16 Mб07582.pdf
#
23.11.20231.16 Mб07583.pdf
#
23.11.20231.16 Mб07584.pdf
#
23.11.20231.16 Mб07585.pdf
#
23.11.20231.16 Mб07586.pdf
#
23.11.20231.16 Mб07587.pdf

ln \| tg \|	ln \| sin \|	ln \| sin \| C ,	(13)
	m