7452

Рис. 1.

Замечание.

1) Всякая точка глобального минимума является и точкой локального миниму-

ма этой функции. Обратное, вообще говоря, неверно.

2)Аналогичные определения глобального максимума и локального максимума можно получить путем замены знака неравенства на противоположный.

3)Если функция обладает свойством унимодальности, то локальный минимум автоматически является глобальным минимумом.

4)Если функция не является унимодальной, то возможно наличие нескольких локальных оптимумов, при этом глобальный минимум можно определить путем нахождения всех локальных оптимумов и выбора наименьшего из них.

Классификация задач оптимизации.

Классификацию задач оптимизации можно проводить по нескольким призна-

кам в зависимости от вида функции f (x) и множества Х:

1)детерминированные, стохастические, задачи оптимизации с неопределенно-

стями; статические, динамические (например, задачи управления);

2)безусловной и условной оптимизации;

3)с непрерывными и дискретными переменными (частично - целочисленные,

целочисленные, с булевыми переменными);

4)однокритериальные и многокритериальные;

5)линейные и нелинейные;

6)одномерные и многомерные, причем многомерные задачи могут быть малой и большой размерности;

7)с выпуклыми и невыпуклыми целевыми функциями;

8)одноэкстремальные и многоэкстремальные.

Нелинейные задачи составляют широкий класс настолько сложных задач, что до сих пор невозможно разработать общие методы, подобные симплекс-методу в линейном программировании, которые позволяли бы решить любые нелинейные за-

дачи. Все возможные методы решения задач нелинейного программирования можно разделить на два больших класса: точные и приближенные методы решения. Точные

11

методы позволяют определить решение для некоторых более узких задач, прежде всего задач с выпуклыми (вогнутыми) функциями F(x) и gi(x). Приближенные (ите-

рационные) методы позволяют решить практически любую задачу нелинейного программирования, однако, имеют свои недостатки: скорость сходимости (число шагов), точность и др.

Алгоритм определения глобального максимума (минимума):

Шаг 1. Приравнять 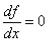и найти все стационарные точки.

Шаг 2. Выбрать все стационарные точки, которые расположены в интервале

[A,B]. Обозначим эти точки через х1, х2, …, хN. Проверку наличия локального опти-

мума следует проводить только на множестве указанных точек, дополненном точ-

ками A и B.

Шаг 3. Найти наибольшее (наименьшее) значение F(х) из множества F(A), F(B), F(х1), …, F(хn). Это значение соответствует глобальному максимуму (минимуму).

Общие сведения о численных методах оптимизации, их классификация.

В большинстве случаев задачу оптимизации: f (x) min , x X не удается ре-

шить опираясь на необходимые и достаточные условия оптимальности или на гео-

метрическую интерпретацию задачи, и приходится ее решать численно с примене-

нием вычислительной техники. Причем, наиболее эффективными оказываются ме-

тоды, разработанные специально для решения конкретного класса задач оптимиза-

ции, так как они позволяют полнее учесть ее специфику.

Любой численный метод имеет два этапа:

1) первый этап любого численного метода (алгоритма) решения задачи опти-

мизации основан на точном или приближенном вычислении ее характеристик (зна-

чений целевой функции; значений функций, задающих допустимое множество, а

также их производных);

2) на втором этапе, на основании полученной информации строится прибли-

жение к решению задачи – искомой точке минимума x* , или, если такая точка не единственна, к множеству точек минимума.

12

Иногда, если только это требуется, строится и приближение к минимальному

значению целевой функции f min f (x) .

x X

Для каждой конкретной задачи вопрос о том, какие характеристики следует вы-

брать для вычисления, решается в зависимости от свойств минимизируемой функ-

ции, ограничений и имеющихся возможностей по хранению и обработки информа-

ции.

В зависимости от того какие характеристики, в частности, целевой функции бе-

рутся, алгоритмы делятся на алгоритмы:

1) нулевого порядка, в них используется информация только о значениях ми-

нимизируемой функции;

2)первого порядка, использующие информацию также и о значениях первых производных;

3)второго порядка, использующие, кроме того, информацию о вторых произ-

водных и так далее.

Когда решен вопрос о том, какие именно характеристики решаемой задачи сле-

дует вычислять, то для задания алгоритма достаточно указать способ выбора точек вычисления. В зависимости от способа выбора точек вычисления, алгоритмы делят-

ся на пассивные и активные (последовательные).

В пассивных алгоритмах все точки выбираются одновременно до начала вы-

числений.

В активных (последовательных) алгоритмах точки вычисления выбираются поочередно, то есть точка xi 1 выбирается, когда уже выбраны точки предыдущих вычислений x1, x2 ,..,xi и в каждой из них произведены предусмотренные алгорит-

мом вычисления, результаты которых будем обозначать соответственно через y1, y 2 ,...,yi .

13

Таким образом, последовательный алгоритм определяется точкой x1 X и на-

числения зависит лишь от точки предыдущего вычисления и полученного результа-

При этом конкретный алгоритм определяется:

1)заданием точки x0 ;

2)правилами выбора векторов h k и чисел k на основе полученной в резуль-

тате вычислений информации;

3) условием остановки.

Правила выбора h k и чисел k могут предусматривать вычисления характери-

стик не только в точках x0 , x1,...,xk , но и в других точках, отличных от x0 , x1,...,xk .

Вектор h k определяет направление k 1-го шага метода минимизации, а коэф-

фициент k – длину этого шага.

Обычно название метода минимизации определяется способом выбора h k , а

его различные варианты связываются с разными способами выбора k .

Наряду с термином шаг метода пользуется также термин итерация метода.

Среди методов минимизации можно условно выделить:

14

конечношаговые методы;

бесконечношаговые методы.

Конечношаговыми (или конечными) называются методы, гарантирующие оты-

скание решения задачи за конечное число шагов.

Для бесконечно шаговых методов достижение решения гарантируется лишь в пределе.

Условия остановки (критерии окончания счета).

Условие остановки может определяться имеющимися в наличии вычислитель-

ными ресурсами (например, числом вычислений характеристик минимизируемой

функции) f (x) .

На практике часто используют следующие условия остановки:

вие стационарности.

2.3.2. Раздел 2. Прикладные нелинейные модели. Условная оптимизация

функции многих переменных. Метод Лагранжа

Постановка задачи и ее особенности.

Задача математического программирования – условный экстремум функции:

15

в которой либо целевая функция, либо ограничения, либо и то и другое нелинейны,

называется задачей нелинейного программирования.

Пусть необходимо найти экстремум функции z f x, при условии, что пере-

менные х и у удовлетворяют уравнению связи x, y 0.

Определение. Говорят, что в точке X 0 x0 , y0 , удовлетворяющей уравнению

летворяют уравнениям связи.

Один из способов определения условного экстремума применяются в том слу-

чае, если из уравнения связи можно выразить одну переменную через другую, тогда,

подставив полученное выражение в функцию z, получим, что z является функцией одной переменной, и задача связана с нахождением глобального экстремума функ-

ции. Такой метод называется методом подстановки.

Метод подстановки

Пример. Предприятие для производства какого-то продукта расходует два средства в количестве х1 и х2 соответственно. (Это факторы производства). Факторы производства взаимозаменяемы. Объем производства является функцией затрат

производства - производная функция. Издержки зависят от расхода обо-

их факторов x1 , x2 и от цен этих факторов c1 , c2 . Совокупные издержки выразятся формулой b c1 x1 c2 x2 . Требуется при данных совокупных издержках определить такое количество факторов производства, которое максимизирует объем производ-

ства.

Математическая модель. Определить х1 и х2, удовлетворяющие условиям

16

лю, при которых

Из теоремы 1 вытекает метод поиска условного экстремума, получивший на-

звание метод Лагранжа.

Схема применения этого метода следующая.

1. Вводится вектор из m дополнительных новых переменных

1 , 2 ,..., m Rm – множителей Лагранжа.

2.Определяется функция Лагранжа

L x, f x g x

или в развернутом виде

L x1,..., xn , 1,..., m f x1,..., xn 1 g1 x1,..., xn ... m gm x1,..., xn

3. Находятся частные производные функции Лагранжа по xj, j 1, n и λi,

i 1, m и приравниваются к нулю:

4. Решается система (2.5) относительно n+m неизвестных x1,..., xn, λ1,..., λm, т.е.

находятся стационарные точки (x*,λ*) функции Лагранжа L(x,λ).

5. Среди точек, подозрительных на экстремум, находят такие, в которых дости-

гается экстремум, и вычисляют значения F(x) в этих точках.

6. Определяют точки максимума и минимума.

Отметим, что условия (2.5) дают лишь необходимые условия экстремума.

Существуют и достаточные условия, определяющие точки максимума или ми-

нимума или отсутствие экстремума. Эти условия определяются знаком второго дифференциала. Если же выполнены достаточные условия, то х* будет точкой ло-

кального экстремума.

18

Пример. На двух предприятиях отрасли необходимо изготовить 200 изделий некоторой продукции. Затраты, связанные с производством х1 изделий на первом предприятии, равны 4х12 руб., а затраты, обусловленные изготовлением х2 изделий на втором предприятии, составляют 20х2 + 6х22 руб. Определить, сколько изделий на каждом из предприятий следует произвести, чтобы общие затраты, обусловленные изготовлением необходимой продукции, были минимальны.

Решение

1. Составим математическую модель.

Замечание. Метод множителей Лагранжа можно применять и в случае, когда ог-

раничения заданы в виде неравенств. При этом следует сначала найти точки безус-

ловного экстремума и среди них выбрать те, которые удовлетворяют ограничениям задачи, затем определить точки, удовлетворяющие системе (1).

Экономический смысл множителей Лагранжа

Рассмотрим теперь важную интерпретацию множителей Лагранжа. Решение системы (2.5) дает, кроме вектора локального экстремума х*, еще и вектор множите-

лей Лагранжа λ*, который несет ценную информацию. Оптимальное значение целе-

вой функции f* = f(х*) зависит от значений констант ограничений bi. Можно дока-

Если интерпретировать F как доход или стоимость, bi – как затраты некоторых ресурсов, то множители Лагранжа будут показывать, как изменится максимальный

19