
7409
.pdf
2) При
x 5
степенной ряд принимает вид
|
|
3 |
|
n |
|||
|
|||
n |
0 |
|
|
, который является
расходящимся по |
достаточному признаку расходимости, поэтому точка |
||
x 5 |
не входит |
в интервал сходимости. Следовательно, |
областью |
сходимости исходного ряда является интервал 5 x 5. |
|
||
Пример 2. Найти область сходимости ряда
|
|
|
|
|
|
(x 2) |
n |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||
|
|
|
|
|
|
(n 1)! |
|
|
|
|
|||
|
|
|
|
|
n 0 |
|
|
|
|
|
|||
|
Решение. |
Данный |
ряд является |
полным степенным рядом. |
|||||||||
радиус сходимости по формуле (3), где |
an |
|
1 |
, an 1 |
1 |
. |
|||||||
(n 1)! |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
(n |
2)! |
||
|
|
|
R lim |
(n 2)! |
lim |
n 2 |
lim (n 2) , |
|
|||||
|
|
|
(n 1)! |
|
|||||||||
|
|
|
n |
n |
|
|
|
n |
|
|
|
||
значит, ряд сходится при всех x R . |
|
|
|
|
|
|
|
|
|||||
|
Пример 3. Найти область сходимости ряда |
|
|
|
|||||||||
|
|
|
|
|
(2n 1)! (x |
7) |
n 1 |
|
|
|
|||
|
|
|
|
. |
|
|
|
||||||
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
Решение. Заданный ряд – полный степенной ряд. Здесь |
an |
|||||||||||
an 1 |
|
(2n 1)! |
. Найдем радиус сходимости по формуле (3): |
|
|
||||||||
(n 1)! |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем
(2n 1)! |
, |
|
n! |
||
|
R lim |
(2n 1)! (n 1)! |
lim |
|
|
n 1 |
lim |
n 1 |
|||||
n! (2n 1)! |
2n (2n 1) |
2n (2n 1) |
||||||||||
n |
n |
n |
||||||||||
следовательно, ряд сходится только в одной точке x 7 . |
||||||||||||
Пример 4. Найти область сходимости ряда |
|
|
||||||||||
|
|
|
(2x 5) |
2n |
|
|
|
|||||
|
|
|
. |
|
|
|||||||
|
|
|
|
n |
2 |
4 |
n |
|
|
|||
|
|
n 0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
Решение. Перепишем данный ряд в следующем виде:
|
2 |
2n |
(x 5 2) |
2n |
|||
|
. |
||||||
|
|
|
n |
2 |
4 |
n |
|
n 0 |
|
|
|
||||
|
|
|
|
|
|||
0 |
, |
Этот ряд является неполным степенным рядом, т.к. содержит только четные степени (x 5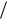 2) . Применим признак Даламбера. Для данного ряда имеем:
2) . Применим признак Даламбера. Для данного ряда имеем:
Найдем
un
lim  n
n
|
2 |
2 |
(x) |
|
|
|
|
u |
n 1 |
(x) |
||
|
|
|||
u |
n |
(x) |
||
|
|
|
|
|
n(x 5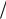 2)2n , n2 4n
2)2n , n2 4n
 :
:
un 1 |
(x) |
22n 2 |
(x 5 2) |
2n 2 |
. |
||
(n 1)2 |
4n 1 |
||||||
|
|
|
|||||
20

|
|
u |
|
(x) |
|
|
2 |
2n 2 |
(x 5 2) |
2n 2 |
n |
2 |
4 |
n |
|
|
|
|
|
|
2 |
2 |
(x 5 2) |
2 |
n |
2 |
||||||||||||||||||
lim |
|
n 1 |
lim |
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
un (x) |
(n 1) |
2 |
4 |
n 1 |
2 |
2n |
(x |
5 2) |
2n |
|
|
(n 1) |
2 |
4 |
|
||||||||||||||||||||||||||||
n |
|
n |
|
|
n |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
(x 5 2) |
2 |
n |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
n |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
lim |
|
|
|
(x 5 2) |
lim |
|
|
|
|
|
(x 5 2) |
. |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
(n 1) |
2 |
|
|
|
|
|
|
(n 1) |
2 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Ряд сходится, |
если |
|
|
(x 5 2) |
2 |
1 или |
|
3 2 x 7 2 |
, и расходится при |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
x 3 2 |
или |
x 7 2 . Исследуем |
|
сходимость |
|
ряда |
|
на |
|
границах интервала |
||||||||||||||||||||||||||||||||||
сходимости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1) |
При |
x 7 2 |
получим обобщенный гармонический сходящийся ряд |
||||||||||||||||||||||||||||||||||||||||
|
1 |
, т.к. |
2 1. Следовательно, |
|
|
точка |
|
x 7 2 |
|
входит в |
|
интервал |
||||||||||||||||||||||||||||||||
|
n |
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
сходимости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2) |
При |
x 3 2 |
получим сходящийся ряд |
|
|
|
|
1 |
|
(см. первый случай). |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
n |
2 |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Точка |
x 3 2 входит в интервал сходимости. |
Значит, |
|
область сходимости |
||||||||||||||||||||||||||||||||||||||||
исходного ряда является отрезком |
3 2 x 7 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Пример 5. Найти область сходимости ряда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
n |
2 |
|
n |
2 |
|
|
8 |
x |
|||||
|
|
||||||
|
|
|
|
||||
n 1 |
|
|
|
|
|
|
.
Решение. Запишем ряд в развернутом виде:
8x 8 |
4 |
x |
4 |
8 |
9 |
x |
9 |
... 8 |
n |
2 |
x |
n |
2 |
... . |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
Очевидно, что бесконечное число его коэффициентов равно нулю, а именно:
a0 a2 a3 a5 a6 a7 |
a8 a10 |
a11 ...am ... 0 |
( m n |
2 |
). Поэтому |
|
формулы (3) и (4) для нахождения радиуса сходимости здесь неприменимы.
Воспользуемся радикальным признаком Коши и найдем |
lim |
n |
|
un (x) |
, где |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
un (x) 8 |
n |
2 |
x |
n |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
n |
un (x) |
lim |
|
|
8 |
n |
2 |
x |
n |
2 |
|
lim |
n |
8 |
n |
2 |
|
|
x |
|
n |
2 |
lim (8 |
n |
|
x |
n |
) |
||||||||||||||||
lim |
n |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
, |
|
если 8 |
x |
|
1, |
или |
|
x |
|
1 8, |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
если 8 |
|
x |
|
1, |
|
или |
|
|
x |
|
1 8, |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0, |
|
если 8 |
|
x |
|
1, |
или |
|
x |
|
1 8. |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Значит, исследуемый ряд сходится при 1 8 x 1
8 x 1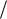 8 . Рассмотрим граничные точки этого интервала.
8 . Рассмотрим граничные точки этого интервала.
1) При x 1 8 имеем ряд 1 1 1 ... 1 ..., который расходится по
8 имеем ряд 1 1 1 ... 1 ..., который расходится по
достаточному признаку расходимости, т.к. lim un lim 1 1 0 . Точка |
|
n |
n |
x 1 8 не входит в интервал сходимости.
8 не входит в интервал сходимости.
21

2) При
x 1 8
8
получим знакочередующийся расходящийся ряд
|
|
n |
2 |
|
|
|
|
( 1) |
1 1 1 1 ... по достаточному признаку расходимости. Точка |
||||
|
||||||
|
|
|||||
n 1 |
|
|
|
|
|
|
x 1 8 |
не входит в интервал сходимости. |
|
||||
|
Таким образом, область сходимости исследуемого ряда – это интервал |
|||||
1 8 x 1 8 . |
|
|||||
|
|
|
|
Свойства степенных рядов |
||
|
Свойство 1. Сумма S(x) степенного ряда (1) является непрерывной |
|||||
функцией в интервале сходимости ( R; R) . |
|
|||||
|
|
|
|
|
|
|
|
Свойство 2. Степенные ряды an xn |
и bn xn , имеющие радиусы |
||||
|
|
|
|
n 0 |
n 0 |
|
сходимости
и умножать. меньше, чем
R1 и R 2 соответственно, можно почленно складывать, вычитать
Радиус сходимости суммы, разности и произведения рядов не меньшее из чисел R1 и R 2 .
Свойство 3. Степенной ряд можно почленно дифференцировать внутри интервала сходимости, при этом для ряда (1)
при
R x R
S (x) a |
|
a x a |
|
x |
2 |
a |
|
x |
3 |
|
|||||
0 |
2 |
|
|
3 |
|
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
выполняется равенство |
|
|
|
|
|
|
|
||||||||
S (x) a |
2a |
|
x 3a |
|
x |
2 |
... |
||||||||
2 |
3 |
|
|||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
... a |
|
x |
n |
||
n |
|
||||
|
|
|
|
|
|
n a |
|
x |
n 1 |
||
n |
|
|
|||
|
|
|
|
|
|
...
...
,
(5)
т.е. сумма ряда, полученного почленным дифференцированием степенного ряда, внутри интервала сходимости равна производной от суммы первоначального ряда.
Из этого свойства следует, что степенной ряд можно почленно дифференцировать внутри интервала сходимости сколько угодно раз.
Свойство 4. Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости, при этом для ряда (1) при R a x R выполняется равенство
x |
|
x |
|
0 |
|
x |
1 |
|
|
S(t) dt |
|
|
|
|
|
||
|
|
a |
|
dt |
|
a |
t dt |
|
a |
|
a |
|
|
|
a |
|
|
x |
2 |
|
|
a2 t |
dt ... |
||
|
|||
a |
|
|
x |
n |
|
an t |
||
|
||
a |
|
dt
...
,
(6)
т.е. сумма ряда, полученного почленным интегрированием степенного ряда, внутри интервала сходимости равна интегралу от суммы первоначального ряда.
Ряды (5) и (6) имеют тот же радиус сходимости, что и исходный степенной ряд (1).
Перечисленные свойства остаются справедливыми и для степенных рядов вида (2).
Свойства степенных рядов широко применяются в приближенных вычислениях и теоретических исследованиях. Так, например, свойства о почленном дифференцировании и почленном интегрировании часто используются для нахождения суммы S(x) функциональных (степенных)
рядов. Если сумму S(x) некоторого ряда трудно найти непосредственно, но легко найти сумму ряда производных (или интегралов), то, дифференцируя
22

(или интегрируя) исходного ряда S(
ряд с известной суммой, можно вычислить и сумму x) .
§6. Разложение функций в степенные ряды
|
|
|
|
|
|
|
|
|
|
Ряды Тейлора и Маклорена |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Для приложений важно уметь данную функцию |
|
f (x) |
раскладывать в |
||||||||||||||||||||||||||||||||||||||||||||||
степенной ряд, т.е. представлять функцию |
|
|
f (x) |
|
в виде суммы степенного |
||||||||||||||||||||||||||||||||||||||||||||
ряда. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для любой функции |
|
|
f (x) , |
определенной в окрестности точки |
x0 и |
||||||||||||||||||||||||||||||||||||||||||||
имеющей в ней производные до |
(n 1) |
|
-го |
|
|
порядка |
|
включительно, |
|||||||||||||||||||||||||||||||||||||||||
справедлива формула Тейлора: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
f (x) |
f (x |
|
) |
|
f |
(x |
0 |
) |
(x x |
|
|
) |
|
f (x |
0 |
) |
|
(x |
|
x |
|
) |
2 |
... |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
1! |
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
(n) |
(x |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
(x x |
|
) |
n |
R |
(x) , |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
n |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
f |
(n 1) |
(c) |
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где Rn (x) |
|
|
|
(x x0 ) |
, |
c |
( x0 |
; x ) |
, |
|
– остаточный член формулы |
||||||||||||||||||||||||||||||||||||||
|
(n 1)! |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тейлора в |
|
форме |
|
Лагранжа. |
Число |
|
|
|
c |
|
|
можно |
записать |
|
в |
виде |
|||||||||||||||||||||||||||||||||
c x0 (x x0 ) , где |
0 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Всякая функция |
f (x) , имеющая производные любых |
|
порядков (т.е. |
||||||||||||||||||||||||||||||||||||||||||||||
бесконечно дифференцируемая) в окрестности |
|
точки |
|
x0 , |
|
может |
быть |
||||||||||||||||||||||||||||||||||||||||||
разложена по степеням |
(x x0 ) : |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
(x |
) |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
f (x |
|
) |
|
|
|
|
|
|
|
|
f (x |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
(n) |
|
|
|
|
|
|
n |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
f (x) f (x |
) |
|
|
|
0 |
|
(x x |
0 |
) |
|
|
|
0 |
|
(x x |
0 |
) |
... |
|
|
|
|
|
0 |
|
(x x ) |
.... (1) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
0 |
|
|
|
1! |
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Разложение (1) функции |
|
f (x) |
по степеням |
|
(x x0 ) |
называется рядом |
|||||||||||||||||||||||||||||||||||||||||||
Тейлора. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что ряд Тейлора формально можно построить для любой |
|||||||||||||||||||||||||||||||||||||||||||||||||
бесконечно дифференцируемой функции |
|
f (x) |
|
в окрестности точки x0 |
(это |
||||||||||||||||||||||||||||||||||||||||||||
необходимое условие). Но отсюда еще не следует, что ряд Тейлора будет сходиться к данной функции f (x) . Он может быть расходящимся или
сходящимся, но не к функции Пример 1. Функция
f (x)
f
(x) . |
|
|
|
|
1 x 2 |
, |
если x 0, |
e |
|
||
|
|
|
|
|
0, |
|
если x 0 |
|
|
|
|
23
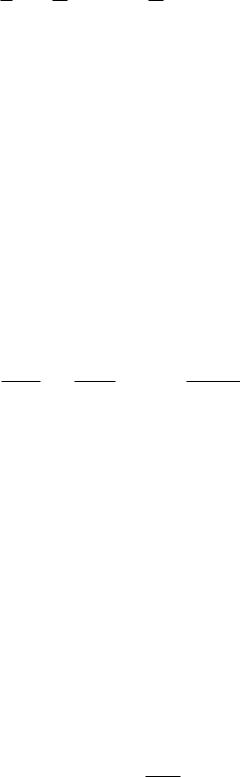
имеет в точке |
x 0 |
производные |
||||
всяком n . Ряд Тейлора имеет вид |
|
|||||
|
|
0 |
0 |
x |
0 |
|
|
|
1! |
2! |
|||
|
|
|
|
|
||
Этот ряд сходится, но его сумма f (x) .
всех порядков, причем |
f |
(n) |
|||||||
|
|||||||||
x |
2 |
... |
0 |
x |
n |
... . |
|
|
|
|
|
|
|
||||||
|
n! |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
S(x) в любой точке |
x равна |
||||||||
(0) 0
нулю,
при
ане
В следующей теореме приведены необходимое и достаточное условия сходимости ряда Тейлора к функции f (x) , порождающей этот ряд.
Теорема. Для того чтобы ряд Тейлора (1), составленный для функции f (x) , сходился к этой функции f (x) в точке x , необходимо и достаточно,
чтобы в этой точке остаточный член формулы Тейлора стремился к нулю при
n , т.е. чтобы lim Rn (x) 0 .
n
Задача разложения функции
f (x)
в степенной ряд, сходящийся к
данной функции f (x) |
, |
сводится к нахождению значений x , при которых |
|
Rn (x) 0 при n . |
|
|
|
В случае, если в |
|
ряде Тейлора (1) |
x0 0 , то получаем разложение |
функции по степеням x |
: |
|
|
|
|
f (0) |
|
f (0) |
|
2 |
|
f |
(n) |
(0) |
|
n |
|
|
|
|
|
|
|
|
|
|
|||
f (x) |
f (0) |
|
x |
|
x |
... |
|
|
|
x |
||
1! |
2! |
|
|
n! |
|
|||||||
|
|
|
|
|
|
|
|
|
||||
Ряд (2) называется рядом Маклорена.
Ряд Тейлора представляет собой степенной ряд вида Маклорена – степенной ряд вида (1) (см. §5).
При разложении функций в ряд Тейлора нужно:
|
|
|
|
|
f |
(n) |
(x) ,…; |
1) найти производные |
f |
(x) , |
f |
(x) ,…, |
|
.... |
(2) |
(2) (см. §5), а ряд
2) вычислить значение функции в точке
точке |
x0 |
; |
x0
и значения производных в
3)составить ряд (1) для заданной функции;
4)найти область сходимости полученного ряда;
5) выяснить, для каких значений x из области сходимости остаточный член ряда Тейлора Rn (x) 0 при n . Если такие значения x найдены, то
для этих значений между функцией f (x) и рядом Тейлора можно поставить
знак равенства.
Замечание. В интервале сходимости степенного ряда остаточный член стремится к нулю при n .
Пример 2. Разложить функцию |
f (x) |
1 |
в ряд Тейлора в окрестности |
|
|||
|
1 |
x |
|
точки |
x0 2 |
. Найти область сходимости полученного ряда. |
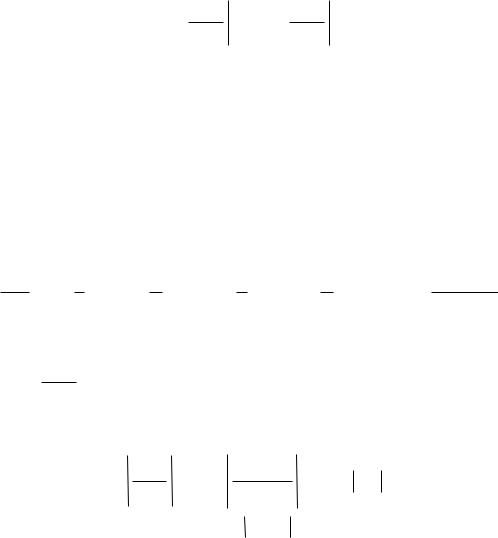
Решение. Находим производные данной функции и вычисляем значение функции и значения производных в точке x0 2 :
24
|
|
f (2) |
1 |
|
|
|
|
|
1 |
|
|
|
|
1, |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
x |
x 2 |
|
x |
1 |
x 2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
f (x) ( (x |
1) |
1 |
) (x 1) |
2 |
, |
|
|
f (2) 1 1!, |
|
|||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
f (x) 2(x 1) |
3 |
2! (x 1) |
3 |
, |
|
f (2) 2!, |
||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
f (x) 2 3 (x 1) 4 |
3! (x 1) 4 , |
|
f (2) 3!, |
|||||||||||||||
f |
IV |
(x) 2 3 4 (x 1) |
5 |
4! (x |
1) |
5 |
, |
f |
IV |
(2) |
4!, |
|||||||||
|
|
|
|
|||||||||||||||||
……………………………………………
f (n) (x) ( 1)n 1 2 3 4 ... n (x 1) (n 1) |
( 1)n 1 n! (x 1) (n 1) , |
|||||
f |
(n) |
(2) |
( 1) |
n 1 |
n!. |
|
|
|
|||||
Составим ряд Тейлора:
f (x)
т.е.
|
1 |
1 |
1! |
(x |
||
|
|
|||||
1 |
x |
|
|
1! |
|
|
1 (x 2) ( |
||||||
f (x) |
1 |
|
|
|||
|
|
|||||
|
|
1 |
x |
|
n 0 |
|
2) |
2! |
(x 2) |
2 |
|
3! |
||||
|
|
|
|
|
|||||
2! |
|
3! |
|||||||
|
|
|
|
|
|||||
x |
2) |
2 |
(x 2) |
3 |
|||||
|
|
||||||||
( 1) |
n 1 |
(x |
2) |
n |
|||||
|
|
|
|
||||||
|
3 |
|
4! |
|
4 |
|
|
( 1) |
n 1 |
n! |
|
||
(x 2) |
|
(x 2) |
... |
|
(x |
||||||||
|
|
|
|
|
|
||||||||
|
4! |
|
|
n! |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
(x 2) |
4 |
... ( 1) |
n 1 |
(x |
2) |
n |
... |
||||||
|
|
|
|||||||||||
.
2) |
n |
... |
|
,
Исследуем сходимость полученного ряда. Для этого найдем его радиус сходимости, т.к. этот ряд является полным степенным рядом.
где
x
a |
n |
( |
|
|
|
|
|
1 |
или |
||
|
1) |
|
|
|
|
|
|
a |
|
|
( 1) |
n 1 |
|
|
|
|
|
R lim |
n |
lim |
|
lim |
1 lim |
1 1, |
|
||||
|
|
|
|
|
||||||||
|
an 1 |
|
n 2 |
|
||||||||
|
|
|
n |
n ( 1) |
n |
n |
|
|
||||
|
|
|
|
|
|
|||||||
1) |
n 1 |
. Ряд сходится при |
x 2 |
1, т.е. 1 x 3, |
и расходится при |
|||||||
|
|
|||||||||||
x 3 |
. Исследуем сходимость ряда на границах этого интервала. |
|
||||||||||
При |
x 1 |
получим |
знакоотрицательный |
ряд |
||||||||
|
|
2n 1 |
|
|
( 1) |
||
|
|||
n 0 |
|
|
1 1 1
...
1
...
, который расходится по свойству, т.к.
расходится соответствующий знакоположительный ряд по достаточному
признаку расходимости ( lim 1 1 0 ). |
|
|||
|
|
n |
|
|
2) При |
x 3 |
получим |
расходящийся |
знакочередующийся ряд |
|
|
|
|
|
( 1)n 1 1 |
1 1 1 1 ... |
по достаточному |
признаку расходимости. |
|
n 0
Следовательно, областью сходимости степенного ряда является интервал
1 x 3 и ряд сходится к функции |
f (x) |
|
1 |
внутри этого интервала. |
|
|
|
||||
|
1 |
x |
|
|
|
Приведем ниже разложения в ряд Маклорена для некоторых элементарных функций, которые в дальнейшем могут быть использованы для разложения многих других функций в ряд Маклорена.
25
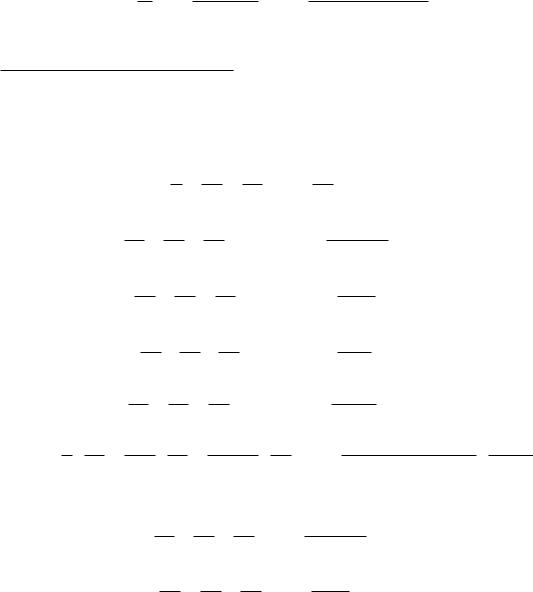
Разложение некоторых элементарных функций в ряд Маклорена
|
(1 x) |
m |
1 |
|
m |
x |
m(m 1) |
x |
2 |
|
m(m 1)(m 2) |
x |
3 |
... |
|||
|
|
|
|
|
|
|
|||||||||||
|
|
1! |
2! |
|
|
|
|
3! |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
m(m 1)(m 2) ... (m n 1) |
|
|
|
|
|
|
[ 1;1], |
если m 0, |
||||||||
|
|
n |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
x |
... , x ( 1;1], если 1 m 0, |
||||||||
|
|
n! |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
( 1;1), |
если m 1, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3)
где |
m |
рядом.
– любое действительное число. Ряд (3) |
|
называется биномиальным |
|||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
x |
|
|
x |
2 |
|
|
x |
3 |
|
|
x |
n |
|
|
|
|
|
|
|
|
|||||
e |
|
1 |
|
|
|
|
|
|
... |
|
|
..., |
x , |
(4) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
1! |
2! |
3! |
n! |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
x |
3 |
|
|
x |
5 |
|
|
x |
7 |
|
|
|
|
|
n |
|
|
|
|
x |
2n 1 |
|
|
|
|||||||||
sin x x |
|
|
|
|
|
|
|
|
... ( 1) |
|
|
|
|
|
|
|
|
..., |
x , |
(5) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
3! |
|
|
|
5! |
|
|
7! |
|
|
|
|
|
|
|
|
|
(2n |
1)! |
|
|
|||||||||||||
|
|
|
|
x |
2 |
|
|
|
|
x |
4 |
|
|
x |
6 |
|
|
|
|
|
n |
|
|
x |
2n |
|
|
|
|||||||
cos x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
... ( 1) |
|
|
|
|
..., |
x , |
(6) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2! |
|
|
4! |
|
6! |
|
|
(2n)! |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
x |
2 |
|
|
|
|
x |
3 |
|
|
x |
4 |
|
|
|
|
|
n |
|
x |
n 1 |
|
|
|
|||||||
ln (1 x) x |
|
|
|
|
|
... ( 1) |
|
|
|
..., |
x ( 1;1], |
(7) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
4 |
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|||||||
|
|
|
|
|
|
x |
3 |
|
x |
5 |
|
arctg x x |
|
|
|
||||||||
3 |
5 |
||||||||||
|
|
|
|
|
|
|
|||||
|
1 |
|
x |
3 |
|
1 3 |
|
x |
5 |
||
arcsin x x |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
|
2 |
|
3 |
|
2 4 |
5 |
|||||
x |
7 |
|
|
|
|
|
n |
|
x |
2n 1 |
|
|
|
|
|
||
|
... ( 1) |
|
|
..., |
x [ 1;1], |
||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||
7 |
|
|
|
|
|
|
|
2n 1 |
|
|
|
|
|
||||
1 3 5 |
|
x |
7 |
|
|
|
|
1 3 5 ... (2n 1) |
|
x |
2n 1 |
||||||
|
|
... |
|
|
|||||||||||||
2 |
4 6 |
7 |
|
2 |
4 |
6 ... (2n) |
2n 1 |
||||||||||
|
|
|
|
|
|
|
|||||||||||
(8)
... |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x [ 1;1], |
||
|
x |
3 |
|
x |
5 |
|
|
x |
7 |
|
|
|
x |
2n 1 |
|
|
||||
sh x x |
|
|
|
|
|
|
|
|
... |
|
|
|
|
..., |
x , |
|||||
3! |
5! |
7! |
(2n 1)! |
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
x |
2 |
|
x |
4 |
|
x |
6 |
|
|
x |
2n |
|
|
|
|||||
ch x 1 |
|
|
|
|
|
... |
|
..., |
x . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2! |
|
4! |
|
6! |
|
(2n)! |
|
|
|
||||||||||
(9)
(10)
(11)
С помощью разложений (3) – (11) можно довольно просто находить разложения многих других функций в ряд Маклорена. Так, например, для
нахождения разложения функции
f (x) sin x |
3 |
|
в ряд Маклорена следует в
равенстве (5) заменить x на x3 . При этом отпадает необходимость исследовать остаточные члены соответствующих формул Тейлора с целью выяснения, можно ли между составленным рядом и самой исходной функцией поставить знак равенства, так как области сходимости табличных рядов известны. Кроме этого, иногда разложение функции в ряд Маклорена получается сложением табличных (ряды (3) – (11)) или ранее найденных разложений, а также с помощью вычитания и умножения известного
разложения |
на |
число. |
Например, |
для |
разложения |
функции |
f (x) (x5 3) cos x |
в ряд Маклорена нужно разложение (6) умножить на x5 |
|||||
и 3 , а затем сложить полученные разложения функций x5 cos x |
и 3cos x . |
|||||
26

Также ряды (3) – (11) используются в комбинации с правилами дифференцирования и интегрирования степенных рядов (см. свойства степенных рядов) для разложения некоторых функций в ряд Маклорена. Так,
при интегрировании известного разложения в ряд Маклорена функции
получается табличное разложение (7).
Пример 3. Разложить функцию |
f (x) 7 |
x |
в ряд Маклорена. |
|
1 1 x
|
|
Решение. |
Воспользуемся |
готовым |
|
разложением |
(4). Так как |
||||||||||||||||||||||||
7 |
x |
e |
ln 7 |
x |
e |
x ln 7 |
, то заменим в разложении (4) |
x |
на xln7 : |
|
|
|
|||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
7x 1 |
x ln 7 |
|
(x ln 7)2 |
|
(x ln 7)3 |
... |
(x ln 7)n |
... |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1! |
|
|
|
2! |
|
|
3! |
|
|
|
|
|
n! |
|
|
|
|||
|
|
|
|
|
ln 7 |
|
|
ln2 |
7 |
|
|
|
|
|
ln3 7 |
|
|
|
lnn 7 |
|
|
|
|
|
lnn 7 |
|
|||||
|
|
1 |
|
|
|
x |
|
|
|
|
x2 |
|
|
|
x3 |
... |
|
|
|
xn ... |
|
|
xn . |
||||||||
|
|
1! |
|
|
2! |
|
3! |
|
n! |
|
|
n! |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|||||||||
Разложение имеет место для |
x , т.к. xln7 |
при x . |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
4 |
|
|
|
|
|
|
|
|
Пример 4. Разложить функцию f (x) cos |
|
в ряд Маклорена. |
|||||||||||||||||||||||||||
|
|
5 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Применим табличное разложение (6), в котором заменим
x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
x |
4 |
|
|
|
(x |
4 |
|
5) |
2 |
|
(x |
4 |
|
5) |
4 |
|
(x |
4 |
|
5) |
6 |
|
|
|
|
n |
|
(x |
4 |
5) |
2n |
|
|
|||||||
|
|
cos |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
... ( 1) |
|
|
|
... |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
5 |
|
|
|
2! |
|
|
|
4! |
|
|
|
6! |
|
|
(2n)! |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
1 |
|
1 |
|
|
x |
8 |
|
|
|
1 |
|
|
|
16 |
|
|
|
1 |
|
x |
24 |
... ( 1) |
n |
|
|
|
1 |
|
x |
8n |
..., |
|||||||||||
|
|
2! 5 |
2 |
|
|
4! 5 |
4 |
x |
|
6! 5 |
6 |
|
|
|
|
(2n)! 5 |
2n |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
x |
4 |
|
|
|
|
|
|
|
n |
|
|
|
1 |
|
|
|
|
|
8n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
т.е. cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
( 1) |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
5 |
|
|
|
|
|
|
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
n 0 |
|
|
|
|
|
(2n)! 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разложение имеет место для x , т.к. |
|
|
|
при x . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
5 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Пример 5. Разложить функцию |
|
f (x) sin |
2 |
3x в ряд Маклорена. |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
x
на
Решение. Так как |
sin2 3x |
1 cos 6x |
|
1 |
|
1 |
cos 6x , то, применив |
|
2 |
2 |
2 |
||||||
|
|
|
|
|
табличное разложение (6) для функции cos 6x , в котором заменим x на 6x , получим:
|
2 |
|
|
|
1 |
|
1 |
|
|
|
|
|
(6x)2 |
|
(6x)4 |
|
(6x)6 |
|
|
|
n |
|
(6x)2n |
|
|
||||||||||
sin |
|
|
3x |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
... ( 1) |
|
|
|
|
... |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
2! |
|
|
4! |
|
|
|
6! |
|
|
|
|
|
|
|
(2n)! |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
62 |
|
|
x2 |
|
64 |
|
|
x4 |
|
66 |
x6 |
... ( 1)n 1 |
|
62n |
|
x2n ... |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
2 2! |
|
|
|
|
|
|
2 4! |
|
|
|
2 6! |
|
|
|
|
|
2 |
(2n)! |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
2n |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 1)n 1 |
|
|
|
|
x2n , |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 (2n)! |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
27

где
x .
Пример 6. Разложить функцию
Решение. Так как
|
|
x |
f (x) ln 2 |
|
|
|
|
7 |
в ряд Маклорена.
|
|
|
x |
|
|
|
1 |
x |
|
|
|
1 |
x |
|
|
|
|
ln |
2 |
|
ln 2 |
|
|
|
ln 2 ln |
|
ln 2 ln 1 |
|
|||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
7 |
|
|
|
14 |
|
|
14 |
|
|
|
||||
то, воспользуемся готовым разложением (7), в котором заменим Тогда получим
x
,
14
|
|
|
x |
|
x |
на |
|
|
. |
|
||||
|
|
|
14 |
|
|
|
x |
|
|
x |
|
( x 14)2 |
|
( x 14)3 |
( x 14) |
4 |
|
|||
ln 2 |
|
|
|
ln 2 |
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
||||||||||
|
|
7 |
|
|
14 |
|
2 |
|
3 |
|
4 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
( x 14)n 1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 1) |
|
|
|
|
|
|
|
|
... |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ln 2 |
1 |
x |
1 |
|
x |
2 |
|
1 |
|
x |
3 |
|
1 |
|
x |
4 |
... |
|
|
|
|
1 |
|
|
x |
n 1 |
... |
|
||||||
14 |
|
2 |
|
|
3 |
|
|
4 |
|
|
|
|
|
|
|
n 1 |
|
|
||||||||||||||||
|
|
2 14 |
|
|
|
3 14 |
|
|
|
|
4 14 |
|
|
|
|
|
|
(n 1) 14 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
xn 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
ln 2 |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
(n 1) 14n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где 1 |
x |
1 |
, т.е |
14 |
x 14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 7. Разложить функцию |
f (x) |
|
5 |
|
в ряд Маклорена. |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
8 x |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Так как
|
5 |
3 |
8 |
|
то применим
x |
7 |
8 : |
|
|
5 (8
x |
7 |
|
табличное
|
|
|
|
|
5 |
|
x |
7 |
|
1 |
|
7 |
|
1 3 |
|
|
|||||
|
|
|
|
|
|
|||||
x |
) |
|
1 |
|
|
|
||||
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|||
разложение (3) при
3 |
5 |
|
|
|
|
|
|||
|
|
|||
|
||||
|
2 |
|
|
|
|
|
|
||
|
|
|
||
m |
1 |
|||
3 |
||||
|
|
|
||
1
,
|
|
x |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
||
заменив
|
1 3 |
|
|
||
|
, |
|
|
||
|
||
|
|
в нем
x
на
|
5 |
3 |
8 |
|
|
|
|
|
5 |
|
|
|
|
|
( 1 3) |
|
|
|
|
x |
7 |
|
|
|
( 1 3) ( 1 3 1) |
|
|
x |
7 |
|
2 |
|
( 1 3) |
( 1 3 1) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
x |
7 |
|
|
2 |
|
|
|
|
|
|
|
1! |
|
|
|
|
|
8 |
|
|
|
|
|
2! |
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3! |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 1 3) ( 1 3 1) ( 1 3 2) |
... ( 1 3 n 1) |
|
|
|
x |
7 |
|
n |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|||
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
1 |
|
|
|
|
|
7 |
|
|
|
|
|
1 4 |
|
|
|
|
14 |
|
|
1 4 7 |
|
|
|
21 |
|
|
|
|
1 4 7 ... (3n 2) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
2 |
|
1 |
|
|
3 |
|
|
x |
|
|
3 |
2 |
2! 8 |
2 |
|
x |
|
|
|
3 |
3! 8 |
3 |
x |
|
|
... |
|
|
3 |
n |
n! 8 |
n |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
( 1 3 2) |
|
|
x |
7 |
|
3 |
|
|
|||||
|
|
|
||||
|
|
|
|
|
||
|
|
|
8 |
|
|
|
|
|
|
|
|
||
x7n ...
28

где
где
|
5 |
|
5 |
|
1 |
x |
7 |
|
5 |
|
|
|
1 4 |
|
x |
14 |
|
5 |
|
|
1 4 7 |
|
x |
21 |
... |
5 |
|
1 4 7 ... (3n 2) |
x |
7n |
... |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
2 |
3 8 |
|
2 |
3 |
2 |
2! 8 |
2 |
|
2 |
3 |
3 |
3! 8 |
3 |
|
2 |
3 |
n |
n! 8 |
n |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
1 4 7 ... (3n 2) |
x |
7n |
, |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
n |
n! 8 |
n |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
1, т.е. |
7 |
|
8 x |
7 |
|
8 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 8. Разложить функцию |
f (x) x |
2 |
arctg x |
|
в ряд Маклорена. |
|||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
Решение. Воспользуемся готовым разложением (8): |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
x |
3 |
|
|
|
x |
5 |
|
x |
7 |
|
|
|
|
|
|
|
n |
|
x |
2n 1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x |
arctg x x |
x |
|
|
|
|
|
|
|
|
|
|
|
... ( 1) |
|
|
|
... |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
5 |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
2n 1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
3 |
|
1 |
|
|
|
|
5 |
|
1 |
|
|
7 |
|
|
1 |
|
9 |
|
|
|
|
|
|
n |
|
|
|
x |
2n 3 |
|
|
||||
|
|
|
|
x |
|
x |
|
x |
|
x |
|
... ( 1) |
|
|
|
..., |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2n 1 |
|
|
|||
1 x 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
§7. Некоторые приложения степенных рядов
1. Приближенное вычисление значений функции
Рассмотрим задачу вычисления значения
заданной точностью 0. |
|
Пусть функция f (x) в интервале |
( R; R |
степенной ряд |
|
функции f (x) при x x1 с
) может быть разложена в
|
f (x) a |
|
a x a |
|
x |
2 |
... |
a |
|
x |
n |
... |
|
0 |
2 |
|
n |
|
|||||||
|
|
1 |
|
|
|
|
|
|
|
|||
и x1 ( R; R ) . Тогда точное значение |
|
f (x1 ) |
равно сумме этого ряда при |
|||||||||
x x1 |
: |
|
|
|
|
|
|
|
|
|
|
|
f (x |
) a |
|
a x |
a |
|
x |
2 |
... a |
|
x |
n |
0 |
2 |
|
n |
|
|||||||
1 |
|
1 1 |
|
1 |
|
1 |
|||||
...
,
а приближенное значение равно частичной сумме |
Sn (x1 ) : |
||
f (x1) Sn (x1 ) a0 |
2 |
|
n |
a1x1 a2 x1 |
... an x1 . |
||
Точность этого приближенного равенства увеличивается с ростом номера n . Абсолютная ошибка приближенного равенства равна модулю остатка
ряда, т.е.
|
f (x1 ) Sn (x1) |
|
rn (x1) |
, |
|
||||
где |
|
|
|
|
|
|
|
|
|
r (x ) a |
xn 1 |
a |
xn 2 |
a |
n |
|
xn 3 |
... . |
|
n 1 |
n 1 1 |
|
n 2 1 |
|
|
3 1 |
|
||
29
