7005

22

Для различных отношений d 2 / d 1 значения ϕ различно. При

<2 значение ϕ близко к единице. Поэтому если толщина стенки трубы по сравнению с диаметром мала или, если отношение d 2 / d 1 близко к единице, влиянием кривизны стенки можно пренебречь.

Для расчета теплопроводности многослойной стенки трубы такая упрощенная формула имеет следующий вид:

где δi – толщина слоя стенки; d m i - средний диаметр; λi

коэффициент теплопроводности; ϕ i - коэффициент кривизны

отдельных слоев.

2 .5 . Теплопроводность шаровой стенки

Рассмотрим полый шар с внутренним радиусом r 1 и

внешним r 2 . Стенка шара состоит из однородного материала,

коэффициент теплопроводности λ, которого постоянен.

Известны температуры внутренней и внешней поверхностей шара t 1 и t 2 , причем t 1 > t 2 ( рис. 6 ) . Изотермические поверхности представляют собой концентрические шаровые поверхности.

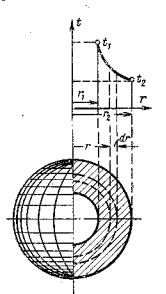
23

Рисунок 6 – Теплопроводность через шаровую однородную стенку

Выделим внутри стенки шаровой слой радиусом r и

толщиной d r ограниченный изотермическими поверхностями.

Согласно закону Фурье тепловой поток, проходящий через этот слой, равен

Разделив переменные, получим

После интегрирования этого уравнения имеем

25

одновременным действием теплопроводности и конвекции.

Явление теплопроводности в жидкостях и газах, так же как и в твердых телах, вполне определяется коэффициентом теплопроводности и температурным градиентом ( см. гл. 1 ) .

Иначе обстоит дело с явлением конвекции - вторым элементарным видом распространения теплоты. Здесь процесс переноса теплоты неразрывно связан с переносом самой среды.

Поэтому конвекция возможна лишь в жидкостях и газах,

частицы которых могут легко перемещаться.

По природе возникновения различают два вида движения

свободное и вынужденное. Свободным называется движение,

происходящее вследствие разности плотностей нагретых и холодных частиц жидкости в гравитационном поле.

Возникновение и интенсивность свободного движения определяются тепловыми условиями процесса и зависят от рода

жидкости, разности температур, напряженности

гравитационного поля и объема пространства, в котором протекает процесс. Свободное движение называется также естественной конвекцией. Вынужденным называется движение,

возникающее под действием посторонних возбудителей,

например насоса вентилятора и пр. В общем случае наряду с вынужденным движением одновременно может развиваться и свободное. Относительное влияние последнего тем больше, чем больше разность температур в отдельных точках жидкости и чем меньше скорость вынужденного движения.

Интенсивность конвективного теплообмена

характеризуется коэффициентом теплоотдачи α с которой

Согласно этому закону тепловой поток Q пропорционален поверхности теплообмена F и разности температур стенки и жидкости (t

26

Коэффициент теплоотдачи можно определить как количество теплоты, отдаваемого в единицу времени единицей поверхности при разности температур между поверхностью и жидкостью,0 равной одному градусу:

В общем случае коэффициент теплоотдачи может изменяться вдоль поверхности теплообмена, и поэтому различают средний по поверхности коэффициент теплоотдачи и

местный ( локальный) коэффициент теплоотдачи,

соответствующий единичному элементу поверхности.

Процессы теплоотдачи неразрывно связаны с условиями

движения жидкости. Как известно, имеются два основных режима течения ламинарный и турбулентный. При ламинарном режиме течение имеет спокойный, струйчатый характер. При турбулентном - движение неупорядоченное, вихревое ( рис. 10 ) .

Изменение режима движения происходит при некоторой

« критической» скорости которая в каждом конкретном случае различна.

В результате специальных исследований О. Рейнольдс в

18 83 г. устоновил, что в общем случае режим течения жидкости определяется не только одной скоростью, а особым безразмерным комплексом w /v , состоящим из скорости движения жидкости w , кинематического коэффициента вязкости жидкости v и характерного размера l: канала или обтекаемого тела. Теперь такой комплекс называется числом Рейнольдса и

обозначается символом R e = w l/v . Переход ламинарного режима в турбулентный происходит при критическом значении этого числа Re кр. Например, при движении жидкости в трубах R e кр = w кр d/v = 2 10 3 .

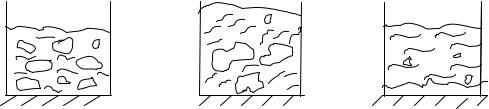
27

Рисунок 10 – Режимы течения жидкостей

При турбулентном движении весь поток насыщен беспорядочно движущимися вихрями, которые непрерывно возникают и исчезают. В точности механизм вихреобразования еще не установлен. Одной из причин их возникновения является потеря устойчивости ламинарного течения, сопровождающаяся образованием завихрений, которые затем диффундируют в ядро и, развиваясь, заполняют весь поток. Одновременно с этим вследствие вязкости жидкости эти вихри постепенно затухают и исчезают. Благодаря непрерывному образованию вихрей и их диффузии происходит сильное перемешивание жидкости,

называемое турбулентным смешением. Чем больше вихрей, тем интенсивнее перемешивание жидкости и тем больше турбулентность. Различают естественную и искусственную турбулентность. Первая устанавливается естественно. Для случая стабилизированного движения внутри гладкой трубы турбулентность вполне определяется значением числа Re .

Вторая вызывается искусственным путем вследствие наличия в потоке каких - либо преград, турбулизирующих решеток и других возмущающих источников. Однако при любом виде турбулентности в тонком слое у поверхности изза наличия вязкого трения течение жидкости затормаживается и скорость падает до нуля. Этот слой принято называть вязким подслое.

Для процессов теплоотдачи режим движения рабочей жидкости имеет очень большое значение, так как им определяется механизм переноса теплоты. При ламинарном режиме перенос теплоты в направлении нормали к стенке в

28

основном осуществляется путем теплопроводности. При турбулентном режиме такой способ переноса теплоты сохраняется лишь в вязком подслое, а внутри турбулентного ядра перенос осуществляется путем интенсивного перемешивания частиц жидкости. В этих условиях для газов и обычных жидкостей интенсивность теплоотдачи в основном определяется термическим сопротивлением пристенного подслоя, которое по сравнению с термическим сопротивлением ядра оказывается определяющим. В этом легко убедиться, если проследить за изменением температуры жидкости в направлении нормали к стенке ( рис. 2 - 2 ) . Как видно, наибольшее изменение температуры происходит в пределах тонкого слоя у поверхности, через который теплота передаe тся путем теплопроводности. Следовательно, как для ламинарного, так и для турбулентного режима течения вблизи самой поверхности применим закон Фурье.

3 .2 . Дифференциальные уравнения теплообмена

Изучить какоелибо явление - значит установить зависимость между величинами, характеризующими это явление. Для сложных явлений, в которых определяющие величины меняются во времени и в пространстве, установить зависимость между переменными очень трудно. В таких случаях, применяя общие законы физики, ограничиваются установлением связи между переменными ( координатами,

временем и физическими свойствами), которая охватывает небольшой промежуток времени и элементарный объем про-

странства. Полученная таким образом зависимость является общим дифференциальным уравнением рассматриваемого процесса. После интегрирования этого уравнения получают аналитическую зависимость между величинами для всей

составлены для любого процесса и, в частности, для процесса теплоотдачи. Так как теплоотдача определяется не только тепловыми, но и гидродинамическими явлениями, то совокупность этих явлений описывается системой дифференциальных уравнений, в которую входят уравнения теплопроводности, уравнение движения и уравнение сплошности.

Дифференциальное уравнение теплопроводности выводится на основе закона сохранения энергии.

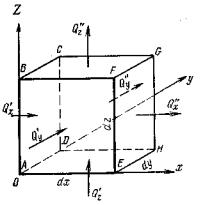
Выделим в движущемся потоке жидкости элементарный параллелепипед с гранями d x , dy и dz и, считая физические параметры λ, ср и ρ постоянными, напишем для него уравнение теплового баланса. Если изменением давления пренебречь, то согласно первому закону термодинамики количество подведенной теплоты равно изменению энтальпии тела.

Рисунок 11 – К выводу дифференциального уравнения теплопроводности