
6906
.pdf
11
функции благодаря выполнению R-функциональных операций средствами функционально-воксельной алгебры.
Так, операции R-функционального пересечения и объединения представимы в виде функционально-воксельных операций сложения, вычитания, взятия модуля и умножения на число. Коэффициент в системе R- функций не меняет нулевых границ, но влияет на поведение значений функции на рассматриваемой области и изменяется на промежутке (−1; 1]. Так, в случае= 0 имеем упрощенное квадратичное выражение операций:
|
|
|
|
|
|
|
= + − √ 2 |
+ 2 |
|
|
|
||||||||
|
|
|
|
{ |
1 |
0 |
2 |
1 |
2 |
|
1 |
|
2 |
|
|
|
|||
|
|
|
|
|
|
0 |
= + + √ 2 |
+ 2 |
|
|
|
||||||||
|
|
|
|
|
1 |
2 |
1 |
2 |
|
1 |
|
2 |
|
|
|
||||
|
А в случае = 1 наблюдается переход от квадратичного, подкорневого |
||||||||||||||||||
выражения к линейному с вычислением по модулю: |
|
|
|
||||||||||||||||
|
1 |
|
|
|
|
|
) = |
1 |
+ 2 |
− | 1 − 2| |
|||||||||
= |
( + − |
√ |
2 + |
2 − 2 |
|||||||||||||||
|
|
|
|
|
|||||||||||||||
1 |
1 |
2 |
2 |
1 |
2 |
|
1 |
2 |
1 |
2 |
|
|
|
|
2 |
|
|||
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
+ 2 |
+ | 1 − 2| |
|||
|
|
|
|
|
|
) = |
|||||||||||||
= |
( + + |
√ |
2 + |
2 − 2 |
|||||||||||||||
|
|
|
|
|
|||||||||||||||
1 |
1 |
2 |
2 |
1 |
2 |
|
1 |
2 |
1 |
2 |
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Таким |
|
образом, |
R-функциональные |
|
операции |
осуществляются |
||||||||||||
посредством вычислений, проводимых над локальными геометрическими
характеристиками 1 |
, 1, 1 |
, 1 и 2, 2, 2, 2 |
функций и |
|
||||||||||||||||||||||||||||
|
1 |
2 |
3 |
|
|
4 |
|
|
|
|
|
|
1 |
|
|
2 |
|
3 |
|
|
|
|
4 |
|
1 |
2 |
||||||
соответственно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Сумма 1+ 2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ 2 |
= 1 2 |
|
+ 2 |
1 |
, = 1,2,4 |
|
||||||||||||||||||||||||
|
|
{ |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||||
|
|
+ |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
|
2 |
|
|
1 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. |
Разность 1−2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1−2 |
= 1 2 |
|
− 2 |
1 |
, = 1,2,4 |
|
||||||||||||||||||||||||
|
|
{ |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||||
|
|
− |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
|
2 |
|
|
1 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Модуль | 1|: |
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3. |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
= − |
|
1 |
|
|
|
− |
|
2 |
− |
|
|
4 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
{ |
|
|
|
|
|
3 |
1 |
|
|
|
|
|
|
3 1 |
|
|
|
|
|
|
3 1 |
|
|
|
||||||
|
|
| 1| |
= − | 1|, = 1,2,4 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4. |
Умножение на число 1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
1 = |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
Возведение в квадрат |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
= − |
|
|
|
|
1 |
|
− |
|
2 |
|
|
− |
4 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
{ |
|
|
|
|
|
|
|
|
|
3 1 |
|
|
|
|
|
|
|
3 1 |
|
|
|
3 1 |
|
||||||
|
|
|
|
2 |
|
= |
|
|
|
, = 1,2,4 |
|
|
|
|||||||||||||||||||
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6. |
Нахождение квадратного корня √ |
1 |
: |
|
|
|
|
|
|
|||||||||||||||||||||||

12
|
|
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|||||
= − |
1 |
− |
|
2 |
|
− |
4 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
1, |
|
|
||||||||
{ |
|
3 1 |
|
|
|
3 |
1 |
|
3 |
|
|
||||||||
√ |
1 |
|
|
1√ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где −локальная функция, 1+ 2 |
, 1−2 – локальные геометрические |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
характеристики суммы и разности функций и , |
| |
| |
, |
– локальные |
|||||||||||||||
|
1 |
|
1 |
||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
||
геометрические характеристики модуля и квадрата функции 1.
Также описана итерационная модель построения функциональновоксельных образов сложной предикатной функции на основе принципа её последовательной композиции, что позволяет значительно ускорить процесс получения решения, не прибегая к рекурсивному вычислению, заложенному в R- функциональном подходе.
Композиционный принцип алгоритма базируется на организации циклического выполнения R-функциональной операции над очередным одномерным ФЛОБом и функционально-воксельной моделью, содержащей результат вычисления предыдущих процедур. Пример поэтапно конструированных кривых приведен на рисунке 4.
Рисунок 4 – Модель итерационного графоаналитического построения ФВмодели параметрической кривой
Применение описанных принципов позволяет значительно увеличить скорость R-функционального построения плоских контуров. Так, построение невыпуклого плоского контура, состоящего из 9 отрезков при размере образа 800×800 с использованием описанных принципов, заняло 111 секунд против 17 минут и 29 секунд при классическом R-функциональном моделировании. Благодаря этому появилась возможность более точного конструирования поверхностей областей моделируемых кривых за счет значительного уменьшения шага параметра t (рис. 5).
Несмотря на это, в случае моделирования кривой предикатным ФЛОБом по-прежнему наблюдается высокая ребристость поверхности, а в случае R- функционального пересечения касательных – нарушение ее непрерывности. Гладкую и монотонную поверхность возможно получить только в случае конструирования кривой посредством одномерного ФЛОБа, что делает его подходящим инструментом для дальнейшего применения.
13
конструирование предикатным ФЛОБом
R-функциональное |
|
пересечение касательных |
конструирование одномерным ФЛОБом |
Рисунок 5 – Повышение гладкости получаемых моделей
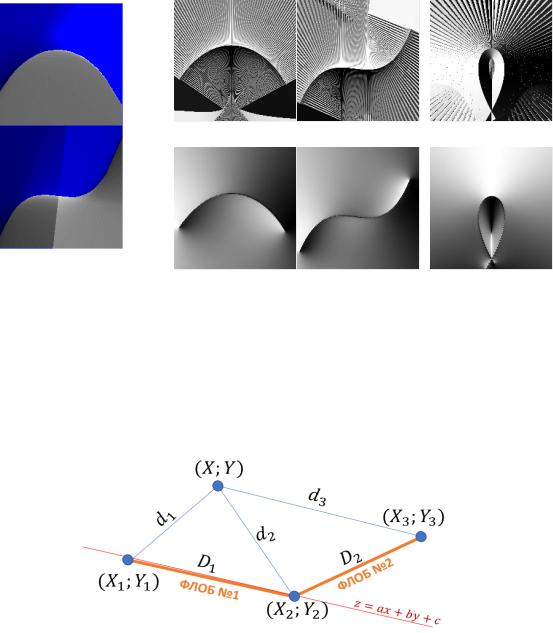
При необходимости на моделях, основанных на вычерчивании нулевого контура на положительной области, возможно выделить отрицательную область функции, для чего необходима разработка дополнительного алгоритма определения инвертируемых по знаку точек. Одним из возможных подходов является определение знака конкретной точки по ближайшему к ней нулевому отрезку, проиллюстрированный на примере двух ФЛОБов на рисунке 6.
Рисунок 6 – Определение знака точки области
Наиближайший к рассматриваемой точке с координатами (, ) нулевой отрезок (ФЛОБ №1 или ФЛОБ №2), определяется сравнением значений всех одномерных функции локального обнуления для текущей точки ( 1 = 1 − (1 + 2) и 2 = 2 − (2 + 3)). Искомый отрезок имеет наименьшее значение функции локального обнуления ( 1 < 2). Знак значения локальной функции в рассматриваемой точке ( , ) будет соответствовать знаку её значения для полуплоскости = + + , проходящей через искомый ближайший отрезок. В случае принадлежности точки отрицательной области данной полуплоскости необходимо осуществить инверсию знака значения локальной функции для данной точки. Вследствие перебора всех точек области локальных функций параметрической кривой формируется ее отрицательная область (рис. 7).

14
Рисунок 7 – Моделирование отрицательной области
Применение предложенных моделей кривых позволяет осуществлять построение более сложных контуров благодаря применению к ним R- функциональных операций (рис. 8). В случае применения моделей, сконструированных посредством ФЛОБов, предварительно необходимо определить отрицательную область кривой.
Рисунок 8 – Построение сложных контуров
Предложенный принцип конструирования области локальных функций также применим не только к кривым Безье любой степени, но и к другим видам параметрических кривых (рис. 9).
а) кривая Безье 10 |
б) лемниската |
в) кубический |
степени |
Бернулли |
B-сплайн |
Рисунок 9 – ФЛОБ-конструирование различных параметрических кривых
В четвертой главе рассмотрены перспективы применения и дальнейшего развития ФЛОБ-конструирования контуров, в том числе содержащих параметрические кривые.
ФЛОБ-конструирование предлагается в решении задачи избегания столкновения группы движущихся мобильных роботов со стенами в ограниченном пространстве. Построенная посредством ФЛОБа функциональновоксельная модель полигона движения роботов содержит внутри контура последовательность экстремальных точек поверхности, приближенных по форме к линейному скелету фигуры. Движение по данной траектории позволит избегать столкновения со стенами полигона, причем, в каждой точке полигона будет известно направление вектора движения к данной траектории. Построение полигонов более сложной формы возможно посредством применения R-
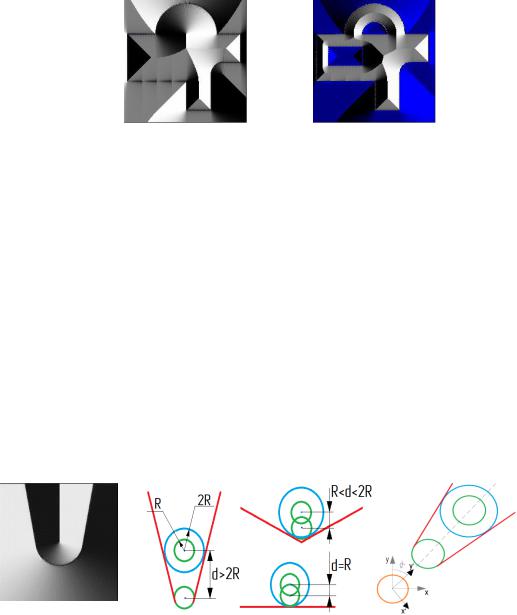
15
функциональных операций к контурам с определяемой отрицательной областью
(рис. 10).
Рисунок 10 – функционально-воксельные модели полигонов
Далее рассмотрена задача нахождения зоны возможного столкновения роботов для алгоритма ORCA. В классическом варианте алгоритма рассматривается определение границ такой зоны с последующим вычислением направления вектора скорости для отклонения курса движения движущихся навстречу роботов.
Очевидно, что при увеличении количества рассматриваемых роботов в сцене, значительно возрастает время вычисления таких параметров. В рассмотренном примере получена функционально-воксельная модель такой зоны, заведомо содержащая в каждой точке информацию об отклонении вектора скорости в виде локальных геометрических характеристик.
Представлена функционально-воксельная модель искомой области в случае статического расположения двух рассматриваемых агентов, а также ее развитие на динамический случай с помощью изменения отклонения от на угол оси направления движения встречного робота и расстояния между роботами (рис. 11).
статичный случай параметры расширения модели на динамический случай
Рисунок 11 – модель статической ситуации искомой области и способы ее расширения на динамический случай
Данная модель рассчитывается заранее, еще до начала процесса движения роботов, заменяя собой часть необходимых для работы алгоритма вычислений. Таким образом уменьшается объем вычислений, производимых в каждый момент времени по отношению к каждой паре рассматриваемых роботов, что позволяет ускорить работу алгоритма.
В результате все возможные варианты искомой области образуют массив, состоящий из двумерных образов статического случая при конкретно задаваемых параметрах, распределенных по координатам и , образуя таким образом четырехмерную модель = { , , , } (рис. 12).

16
Для принятия решения о направлении движения роботу необходимо выбрать из данного массива необходимый плоский образ по параметрам и и все оставшиеся вычисления проводить на основе локальных геометрических характеристик, получаемых по координатам и используемого образа.
ФЛОБ-конструирование также предлагается использовать в области механической обработки резанием. Задача автоматизированного построения траектории движения фрезы при вытачивании карманных заглублений сложной формы является актуальной в условиях промышленной цифровизации и возрастающих требований к точности получаемых деталей. Модели,
построенные с помощью ФЛОБов, подходят для получения траектории движения в направлении перпендикулярном градиентному спуску (рис. 13). Так обеспечивается постепенное заполнение моделируемой внутренней области контура спиралью от экстремальной точки к границам.
Разбиение сложного контура на более простые составляющие с последующим их объединением при помощи R-функций, обеспечивает корректное заполнение. Также в зависимости от формы подконтуров может потребоваться применение как линейной, так и квадратичной реализации операции пересечения нулевых отрезков. Помимо этого, управлять формой
получаемой траектории можно заданием шага смещения по траектории спирали и корректировкой геометрии образуемой карманной поверхности за счет умножения на коэффициент значений локальной функции отдельных компонентов контура.
Также рассмотрена возможность применения ФЛОБа в трехмерном моделировании. Если при двумерном моделировании ФЛОБ является отрезком на положительной плоской области значений, то в трехмерном случае ФЛОБ будет являться плоским треугольным элементом, расположенным в положительном трехмерном пространстве значений (двумерный ФЛОБ). Двумерный ФЛОБ будет определяться сравнением своей площади с суммой остальных площадей образуемых треугольников. Таким образом, двумерный
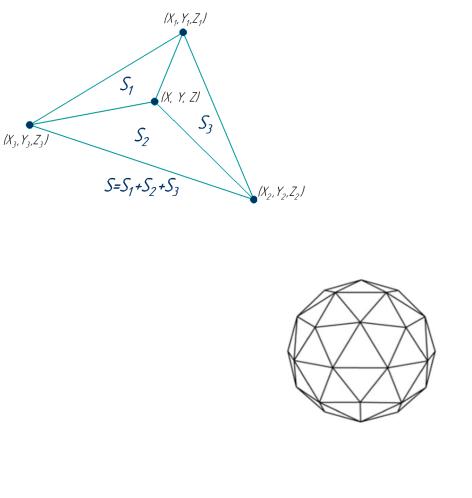
|
17 |
|
ФЛОБ, заданный точками |
( 1, 1, 1), (2, 2, 2) и (3, 3, 3) будет |
|
определяться выражением: |
|
|
2 |
= 1 + 2 + 3 − ∆ |
|
где ∆ – площадь двумерного ФЛОБа, |
1, 2, 3 – площади треугольников, |
|
образованных текущей точкой |
( , , ) и |
перебором вершин треугольного |
ФЛОБа (рис. 14).
Анализ применения ФЛОБа в трехмерном моделировании проведен на известном и геометрически предсказуемом уравнении сферы:
= 1 − 2 − 2 − 2
Рисунок 14 – схема трехмерного ФЛОБа
Для моделирования данной сферы посредством двумерного ФЛОБа необходимо ее разбиение на правильные треугольники (рис. 15). Каждый из этих треугольников будет моделироваться двумерным ФЛОБом. Их последовательное R-функциональное пересечение позволит моделировать поверхность всей сферы. С увеличением количества треугольников в модели повышается точность её представления, но при этом возрастают требуемые вычислительные и временные ресурсы.
На рисунке 16 приведено сравнение двух функционально-воксельных моделей сферы, представленных в порождённых М-образах отношения компонентов нормали:
модели, полученной классическим функционально-воксельным моделированием и модели, полученной ФЛОБ-конструированием после триангуляции.
На изображении наблюдается в целом совпадение поведения функции с высокой точностью. Это говорит о правомерности применения ФЛОБа в дискретном трехмерном моделировании пространства функции.

18
Классическая
модель
М |
М |
М |
М |
1 |
2 |
2 |
2 |
ФЛОБконструирование (80 треугольников)
М |
М |
М |
М |
1 |
2 |
2 |
2 |
Рисунок 16 – Сравнение ФВ-моделей сферы
Основные результаты и выводы
1.Разработанный принцип конструирования R-функциональных операций, основанный на применении функционально-воксельной алгебры, позволяет осуществлять R-функциональные операции над функциональновоксельными моделями областей функций посредством алгебраических операций над их локальными характеристиками. При этом отсутствует необходимость в проведении на каждом этапе вычислений переапроксимации результирующей области, требуемой при реализации R-функциональных процедур в классическом варианте.
2.Разработанная итерационная модель построения функциональновоксельных образов сложной предикатной функции основывается на принципе последовательной композиции расчёта такой функции. Это подразумевает пошаговое наращивание областей сложной предикатной функции из ее более простых составляющих с сохранением промежуточных этапов вычислений. Таким образом построение осуществляется итерационно, не требуя повторного расчета уже смоделированных областей. Благодаря этому удается ускорить процесс поиска решения по сравнению с классическим R-функциональным подходом, требующим рекурсивных вычислений.
3.Разработанный алгоритм генерации локальных функций прямоугольной области, основанный на последовательном R-функциональном пересечении функций локального обнуления, позволяет промоделировать области локальных функций для параметрически заданной функции. При этом возможно задание знака полученных областей посредством определения наиближайшего сегмента нуль-границы к рассматриваемой точке. Таким образом появляется возможность применения функционально-воксельных моделей к параметрическим функциям
сдальнейшим применением в R-функциональном моделировании, что значительно расширяет возможности теоретико-множественного моделирования в построении сложных нуль-границ для геометрического объекта.
19
4.Разработанная четырехмерная модель области возможного столкновения двух мобильных роботов, основанная на пространственновременном распределении двумерных статических функционально-воксельных моделей, позволяет сократить затрачиваемое на вычисление вектора избегания столкновения время за счет предварительного расчета и сохранения локальных геометрических характеристик моделируемой области в графические образы, заранее реализуя часть вычислений в алгоритме ORCA.
5.Разработанный принцип моделирования траектории движения режущего инструмента для механической обработки карманов сложной формы, основанный на применении локальных геометрических характеристик функционально-воксельной модели, позволяет автоматически заполнять внутреннее пространство замкнутого контура от экстремальной точки карманной поверхности по спирали к заданной границе. Появляется дополнительная возможность использовать полученный принцип для решения технологической задачи фрезеровки карманов на основе применения функционально-воксельной модели в процессе проектирования.
Публикации по теме диссертационной работы
Статьи, опубликованные в изданиях, рекомендованных ВАК:
1. Функционально-воксельное моделирование кривой Безье / М. А. Локтев, А. И. Разумовский, А. А. Сычева, П. М. Харланова // Перспективы науки. – 2020. – № 11(134). – С. 196-198.
2.Моделирование алгоритмов управления группами мобильных роботов средствами функционально-воксельного метода / А. В. Толок, М. А. Локтев, А. А. Сычева [и др.] // Станкоинструмент. – 2020. – № 4(21). – С. 76-81. – DOI: 10.22184/2499-9407.2020.21.04.76.81.
3.Сычева, А. А. Функционально-воксельное моделирование кривых Безье
/А. А. Сычева // Геометрия и графика. – 2021. – Т. 9, № 4. – С. 63-72. – DOI: 10.12737/2308-4898-2022-9-4-63-72.
4.Сычева, А. А. Функционально-воксельное моделирование областей столкновения роботов / А. А. Сычева, А. В. Толок // Управление большими системами: сборник трудов. – 2022. – № 98. – С. 60-78. – DOI: 10.25728/ubs.2022.98.4.
Статьи, опубликованные в изданиях, индексированных Scopus:
5.Tolok, A. Construction of the functional voxel model for a spline curve / A. Tolok, N. Tolok, A. Sycheva // CEUR Workshop Proceedings: 30, Saint Petersburg, 22–25 сентября 2020 года. – Saint Petersburg, 2020. – DOI: 10.51130/graphicon- 2020-2-3-52.
6.Tolok, A. V. Building a space for an analytic function that describes a spline curve / A. V. Tolok, M. A. Loktev, A. A. Sycheva // IOP Conference Series: Materials Science and Engineering, Sevastopol, 07–11 сентября 2020 года. – Sevastopol, 2020.
– P. 032091. – DOI: 10.1088/1757-899X/971/3/032091.
7.Tolok, A. Geometric aspects of the functional-voxel implementation of the ORCA algorithm / A. Tolok, A. Sycheva // CEUR Workshop Proceedings: 31, Nizhny
20
Novgorod, 27–30 сентября 2021 года. – Nizhny Novgorod, 2021. – P. 637-644. – DOI: 10.20948/graphicon-2021-3027-637-644.
8. Shutova, K. Using a Functional Voxel Model to Simulate Swarm Motion of a Multi-agent System in a Confined Space / K. Shutova, A. Sycheva // Technologies for Smart Cities. – Cham, Switzerland: Springer Cham, 2022. – P. 21-30. – DOI: 10.1007/978-3-031-05516-4_2.
Статьи в сборниках научных трудов и конференций:
9.Толок, А. В. Функционально-воксельное моделирование областей столкновения роботов / А. В. Толок, А. А. Сычева // Управление большими системами: труды XVII Всероссийской школы-конференции молодых ученых, Москва-Звенигород, 06–09 сентября 2021 года. – Москва: Институт проблем управления им. В. А. Трапезникова РАН, 2021. – С. 361-374. – DOI: 10.25728/ubs.2021.035.
10.Сычева, А. А. Функционально-воксельное моделирование траектории движения инструмента при фрезеровании карманной области / А. А. Сычева, А. М. Плаксин // Труды Международной конференции по компьютерной графике и зрению "Графикон". – 2022. – № 32. – С. 892-898. – DOI: 10.20948/graphicon-2022-892-898.
11.Сычева, А. А. Компьютерное моделирование функции сферы методом функционально-воксельного моделирования / А. А. Сычева, А. В. Толок // Управление большими системами: труды XVIII Всероссийской школыконференции молодых ученых, Челябинск, 05–08 сентября 2022 года / Министерство науки и высшего образования Российской Федерации ЮжноУральский государственный университет Институт проблем управления им. В.А. Трапезникова Российской академии наук. – Челябинск: Издательский центр ЮУрГУ, 2022. – С. 375-383.
Свидетельства о регистрации программы для ЭВМ:
12. Свидетельство о государственной регистрации программы для ЭВМ №
2021616014 Российская Федерация. Расчетный модуль определения физических характеристик в процессе технологической обработки изделий на основе функционально-воксельного моделирования: № 2021615068: заявл. 09.04.2021: опубл. 15.04.2021 / А. М. Плаксин, С. А. Пушкарев, А. В. Толок [и др.]; заявитель федеральное государственное бюджетное образовательное учреждение высшего образования «Московский государственный технологический университет «СТАНКИН».
